Решение
Задание №19. Умение анализировать алгоритм логической игры.
Задание №20. Умение найти выигрышную стратегию игры.
Задание №21. Умение построить дерево игры по заданному алгоритму и найти выигрышную стратегию.
Уровень сложности - повышенный, максимальный балл за выполнение каждого задания - 1, общее время на выполнение трёх заданий - 22 минуты.
№19. Два игрока, Петя и Ваня, играют в следующую игру. Перед игроками лежит куча камней. Игроки ходят по очереди, первый ход делает Петя. За один ход игрок может добавить в кучу один или четыре камня либо увеличить количество камней в куче в пять раз. Например, имея кучу из 15 камней, за один ход можно получить кучу из 16, 19 или 75 камней. У каждого игрока, чтобы делать ходы, есть неограниченное количество камней. Игра завершается в тот момент, когда количество камней в куче становится не менее 73.
Победителем считается игрок, сделавший последний ход, т.е. первым получивший кучу, в которой будет 73 или больше камней.
В начальный момент в куче было S камней; 1 ≤ S ≤ 72.
Будем говорить, что игрок имеет выигрышную стратегию, если он может выиграть при любых ходах противника. Описать стратегию игрока – значит описать, какой ход он должен сделать в любой ситуации, которая ему может встретиться при различной игре противника.
Укажите такое значение S, при котором Петя не может выиграть за один ход, но при любом ходе Пети Ваня может выиграть своим первым ходом. Назовите минимальное значение S, при котором это возможно.
Разбор задания №19. Из условия мы знаем, что Петя не может выиграть своим первым ходом, но Ваня, независимо от хода Пети, выигрывает. Петя парень не глупый и, естественно, сделает самый маленький ход – добавит в кучу один камень (S+1), чтобы Ваня от выигрыша был как можно дальше. Далее Ваня делает свой первый ход и выигрывает. Ване необходимо максимально увеличить предыдущее значение камней в куче, следовательно, Ваня увеличивает количество камней в куче в пять раз (S+1)*5. Теперь просто решаем неравенство:
(S+1)*5 ≥ 73
5S+5≥ 73
5S ≥ 73-5
5S ≥ 68
S ≥ 68:5
S ≥ 13,6
S = 14
Ответ: 14.
№20. Для игры, описанной в предыдущем задании, укажите два таких значения S, при которых у Пети есть выигрышная стратегия, причём одновременно выполняются два условия:
· Петя не может выиграть за один ход;
· Петя может выиграть своим вторым ходом независимо от того, как будет ходить Ваня.
Найденные значения запишите в порядке возрастания.
Разбор задания №20. Здесь мы должны найти два значения S – наибольшее и наименьшее. Начнём с наибольшего (это проще). По условию Петя не выигрывает своим первым ходом, но он же его делает! Следовательно, Петя ходит минимальный ход, чтобы Ваня был максимально далёк от победы (S+1). Далее ходит Ваня, а он тоже парень не глупый и старается не дать Пете победить и делает минимальный ход (S+1)+1. Теперь Петя делает максимально возможный ход, чтобы победить – он увеличивает предыдущее значение камней в куче в пять раз ((S+1)+1)*5. Решаем неравенство:
((S+1)+1)*5 ≥ 73
(S+2)*5 ≥ 73
5S+10 ≥ 73
5S ≥ 73-10
5S ≥ 63
S ≥ 63:5
S ≥ 12,6
S = 13
Теперь определим наименьшее значение S. Мы только что определили, что при S = 13 Петя делает свой ход и количество камней в куче становиться равным 14. То есть из этой позиции Петя точно выигрывает, независимо от того, как будет ходить Ваня. А как ещё после первого хода Пети в куче можно получить количество камней равное 14? По условию мы можем добавить один камень или четыре или увеличить их количество в пять раз. Четырнадцать на пять не делится (камни у нас целые числа), а вот отнять от четырнадцати четыре можно. Следовательно, 14 – 4 = 10. Это минимальное количество камней в куче, при котором Петя может выиграть своим вторым ходом независимо от того, как будет ходить Ваня.
Ответ: 1013.
№21. Для игры, описанной в задании 19, найдите минимальное значение S, при котором одновременно выполняются два условия:
· у Вани есть выигрышная стратегия, позволяющая ему выиграть первым или вторым ходом при любой игре Пети;
· у Вани нет стратегии, которая позволит ему гарантированно выиграть первым ходом.
Разбор задания №21. При решении этого задания мы будем опираться на уже известные нам данные, полученные из предыдущего задания. Мы знаем, что при S = 10 Петя выигрывает, а по условию должен выиграть Ваня своим вторым ходом, следовательно, достаточно уменьшить это значение на единицу: 10 – 1 = 9. После первого хода Петя увеличивает количество камней на один 9 + 1 = 10, далее Ваня увеличивает количество камней в куче на четыре 10 + 4 = 14. Позиция 14 – это выигрышная позиция, нам это известно из предыдущих заданий.
Ответ: 9.
Еще один вариант решения подобного задания
Два игрока, Петя и Ваня, играют в следующую игру. Перед игроками лежат две кучи камней. Игроки ходят по очереди, первый ход делает Петя. За один ход игрок может добавить в одну из куч (по своему выбору) один камень или увеличить количество камней в куче в два раза. Например, пусть в одной куче 10 камней, а в другой 5 камней; такую позицию в игре будем обозначать (10, 5). Тогда за один ход можно получить любую из четырёх позиций: (11, 5), (20, 5), (10, 6), (10, 10). Для того чтобы делать ходы, у каждого игрока есть неограниченное количество камней.
Игра завершается в тот момент, когда суммарное количество камней в кучах становится не менее 63. Победителем считается игрок, сделавший последний ход, т.е. первым получивший такую позицию, при которой в кучах будет 63 или больше камней.
В начальный момент в первой куче было пять камней, во второй куче – S камней; 1 ≤ S ≤ 57.
Будем говорить, что игрок имеет выигрышную стратегию, если он может выиграть при любых ходах противника. Описать стратегию игрока – значит описать, какой ход он должен сделать в любой ситуации, которая ему может встретиться при различной игре противника. В описание выигрышной стратегии не следует включать ходы играющего по этой стратегии игрока, не являющиеся для него безусловно выигрышными, т.е. не являющиеся выигрышными независимо от игры противника.
Решение:

Ответ: 15
20. Для игры, описанной в предыдущем задании, найдите два таких значения S, при которых у Пети есть выигрышная стратегия, причём одновременно выполняются два условия:
— Петя не может выиграть за один ход;
— Петя может выиграть своим вторым ходом независимо от того, как будет ходить Ваня.
Найденные значения запишите в ответе в порядке возрастания.
Решение в Exel:
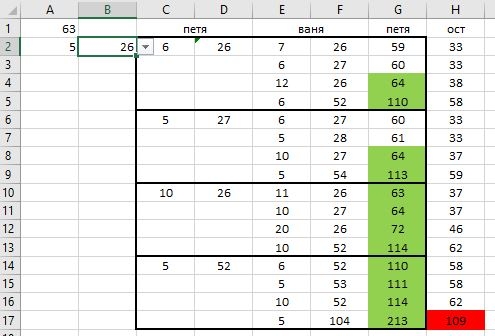
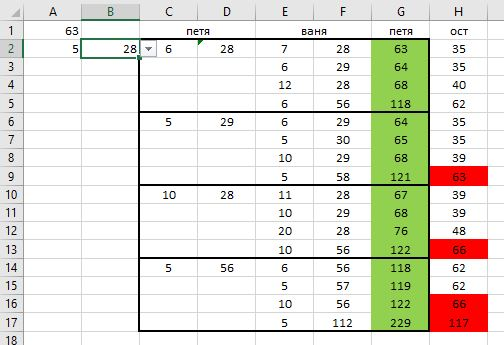
Ответ: 26; 28
21. Для игры, описанной в задании 19, найдите минимальное значение S, при котором одновременно выполняются два условия:
— у Вани есть выигрышная стратегия, позволяющая ему выиграть первым или вторым ходом при любой игре Пети;
— у Вани нет стратегии, которая позволит ему гарантированно выиграть первым ходом.
Решение в Exel:
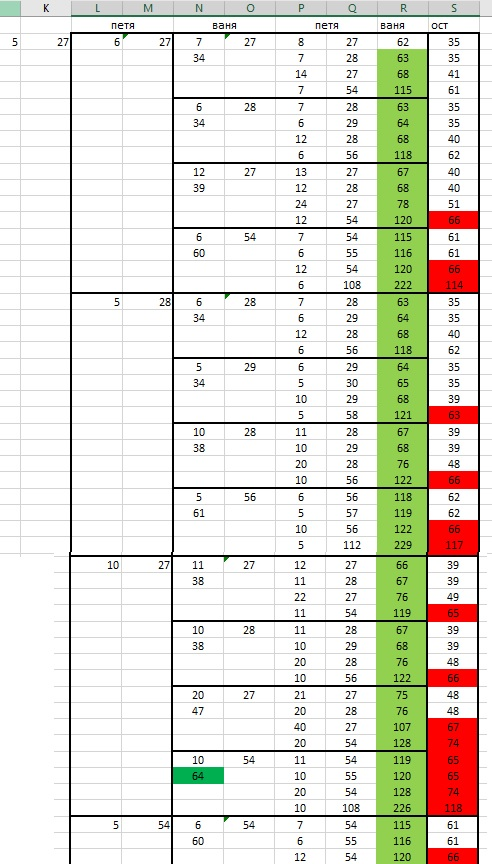
Ответ: 27
https://www.youtube.com/watch?v=XP6rDzb1t30
https://www.youtube.com/watch?v=bTqqdf3WQ1g