1. Наибольшее распространение в эконометрических исследованиях получили:
в) системы взаимозависимых уравнений.
2. Эндогенные переменные – это:
б) зависимые переменные, число которых равно числу уравнений в системе и которые обозначаются через  ;
;
3. Экзогенные переменные – это:
а) предопределенные переменные, влияющие на зависимые переменные, но не зависящие от них, обозначаются через  ;
;
4. Лаговые переменные – это:
в) значения зависимых переменных за предшествующий период времени.
5. Для определения параметров структурную форму модели необходимо преобразовать в:
а) приведенную форму модели;
6. Модель идентифицируема, если:
в) если число параметров структурной модели равно числу параметров приведенной формы модели.
7. Модель неидентифицируема, если:
а) число приведенных коэффициентов меньше числа структурных коэффициентов;
8. Модель сверхидентифицируема, если:
б) если число приведенных коэффициентов больше числа структурных коэффициентов;
9. Уравнение идентифицируемо, если:
б)  ;
;
10. Уравнение неидентифицируемо, если:
а)  ;
;
11. Уравнение сверхидентифицируемо, если:
в)  .
.
12. Для определения параметров точно идентифицируемой модели:
а) применяется двушаговый МНК;
13. Для определения параметров сверхидентифицируемой модели:
б) применяется косвенный МНК;
14. Для определения параметров неидентифицируемой модели:
б) ни один из существующих методов применить нельзя.
Временные ряды
1. Аддитивная модель временного ряда имеет вид:
б)  ;
;
2. Мультипликативная модель временного ряда имеет вид:
а)  ;
;
3. Коэффициент автокорреляции:
а) характеризует тесноту линейной связи текущего и предыдущего уровней ряда;
4. Аддитивная модель временного ряда строится, если:
а) значения сезонной компоненты предполагаются постоянными для различных циклов;
5. Мультипликативная модель временного ряда строится, если:
б) амплитуда сезонных колебаний возрастает или уменьшается;
6. На основе поквартальных данных построена аддитивная модель временного ряда. Скорректированные значения сезонной компоненты за первые три квартала равны: 7 – I квартал, 9 – II квартал и –11 – III квартал. Значение сезонной компоненты за IV квартал есть:
а) 5;
7. На основе поквартальных данных построена мультипликативная модель временного ряда. Скорректированные значения сезонной компоненты за первые три квартала равны: 0,8 – I квартал, 1,2 – II квартал и 1,3 – III квартал. Значение сезонной компоненты за IV квартал есть:
а) 0,7;
8. Критерий Дарбина-Уотсона применяется для:
а) определения автокорреляции в остатках;
Вопросы к зачету
1. Определение эконометрики. Эконометрический метод и этапы эконометрического исследования.
Эконометрикой называется наука, позволяющая анализировать связи между различными экономическими показателями на основании реальных статистических данных с применением методов теории вероятностей и математической статистики. Эконометрические методы (англ. econometric methods of evaluation) представляют собой не экспериментальные методы оценивания и заключаются в совместном применении математического, статистического и экономического инструментария к анализу эмпирических данных с целью оценки эффекта программы.
Самым очевидным способом оценки изменений, произошедших в ходе реализации программы, являлось бы сравнение параметров двух состояний для каждого бенефициара: до и после проведения программы (например уровень образования индивида до и после проведения государством образовательной программы). Однако никто, чаще всего, не обладает таким массивом информации, так как до начала реализации программы средства на сбор подобных данных, как правило, не выделяются. Использование же эконометрических методов без привлечения значительных средств позволяет «оценить, что было бы, если бы индивид не участвовал в программе, то есть „рассчитать“ условное значение (англ. counterfractual) интересующего нас параметра в отсутствие программы» на основании данных только лишь одного периода.
В число эконометрических методов оценивания входят:
· метод сравнения средних,
· построение уравнения регрессии методом наименьших квадратов (англ. OLS),
· метод подбора контрольной группы (англ. matching),
· метод подбора контрольной группы по индексу соответствия (англ. propensity score matching),
· метод построения регрессии с переключением режимов (англ. switching regression)
Выделяют семь основных этапов эконометрического моделирования:
1) постановочный этап, в процессе осуществления которого определяются конечные цели и задачи исследования, а также совокупность включённых в модель факторных и результативных экономических переменных. При этом включение в эконометрическую модель той или иной переменной должно быть теоретически обоснованно и не должно быть слишком большим. Между факторными переменными не должно быть функциональной или тесной корреляционной связи, потому что это приводит к наличию в модели мультиколлинеарности и негативно сказывается на результатах всего процесса моделирования;
2) априорный этап, в процессе осуществления которого проводится теоретический анализ сущности исследуемого процесса, а также формирование и формализация известной до начала моделирования (априорной) информации и исходных допущений, касающихся в частности природы исходных статистических данных и случайных остаточных составляющих в виде ряда гипотез;
3) этап параметризации (моделирования), в процессе осуществления которого выбирается общий вид модели и определяется состав и формы входящих в неё связей, т. е. происходит непосредственно моделирование.
К основным задачам этапа параметризации относятся:
а) выбор наиболее оптимальной функции зависимости результативной переменной от факторных переменных. При возникновении ситуации выбора между нелинейной и линейной функциями зависимости, предпочтение всегда отдаётся линейной функции, как наиболее простой и надёжной;
б) задача спецификации модели, в которую входят такие подзадачи, как аппроксимация математической формой выявленных связей и соотношений между переменными, определение результативных и факторных переменных, формулировка исходных предпосылок и ограничений модели.
4) информационный этап, в процессе осуществления которого происходит сбор необходимых статистических данных, а также анализируется качество собранной информации;
5) этап идентификации модели, в ходе осуществления которого происходит статистический анализ модели и оцененивание неизвестных параметров. Данный этап непосредственно связан с проблемой идентифицируемостимодели, т. е. ответа на вопрос «Возможно ли восстановить значения неизвестных параметров модели по имеющимся исходным данным в соответствии с решениная процедура оценивания неизвестных параметров модели по имеющимся исходным данным;
6) этап оценки качества модели, в ходе осуществления которого проверяется достоверность и адекватность модели, т. е. определяется, насколько успешно решены задачи спецификации и идентификации модели, какова точность расчётов, полученных на её основе. Построенная модель должна быть адекватна реальному экономическому процессу. Если качество модели является неудовлетворительным, то происходит возврат ко второму этапу моделирования;
7) этап интерпретации результатов моделирования.
1. Парная регрессия. Способы задания уравнения парной регрессии
Парная регрессия представляет собой уравнение, описывающее связь между двумя переменными: зависимой переменной и независимой переменной. Иногда переменную называют результатом, а переменную – фактором:, при этом функция может быть как линейной, так и нелинейной.
В парной регрессии выбор вида математической функции  может быть осуществлен тремя методами:
может быть осуществлен тремя методами:
Аналитический метод (теоретический анализ связи рассматриваемого фактора и результата); 2) Графический метод (строится поле корреляции); 3) Экспериментальный метод- основной (например, рассчитываются коэффициенты детерминации или ошибки).
Линейная модель парной регрессии. Смысл и оценка параметров.
Линейная модель парной регрессии есть: у=bх+a+e
b - коэф-т регрессии, показывающий, как изменится у при изменении х на единицу
a - это свободный член, расчетная величина, содержания нет.
e - это остаточная компонента, т.е. случайная величина, независимая, нормально распределенная, мат ожид = 0 и постоянной дисперсией.
1)Теоретический. Считается, что определена генеральная совокупность. Зная те или иные статистические свойства этой совокупности, можно теоретически определить параметры модели. 2) Эмпирический. Исследователь использует лишь выборочные данные. На этом этапе можно оценить, но нельзя точно определить значения параметров модели, поскольку они являются случайными величинами. Согласно выборочному методу статистики характеристики генеральной совокупности принято называть параметрами, а характеристики выборочной совокупности – оценками. Оценка генеральных параметров может быть получена двумя методами: а) методом наименьших квадратов (МНК), б) методом максимального правдоподобия. Свойства оценки: несмещенность (оценка является несмещенной, если мат.ожидание оценки равно оцениваемому параметру при любом объеме выборки, т. е.оценка должна в среднем соответствовать выбранному параметру), эффективность (несмещенная оценка называется эффективной, если она имеет минимальную дисперсию по сравнению с другими выборочными оценками), состоятельность (оценка наз-ся состоятельной, если при увеличении объема выборки оценка стремится к оцениваемому параметру). Для оценки параметров функций, линейных по параметрам, используется метод наименьших квадратов (МНК). МНК позволяет получить такие оценки параметров, при которых сумма квадратов отклонений фактических значений результативного признака от теоретических минимальна:  . Для линейных и нелинейных уравнений, приводимых к линейным, решается следующая система относительно a и b:
. Для линейных и нелинейных уравнений, приводимых к линейным, решается следующая система относительно a и b:
Σу=na+bΣx
Σyx=aΣx+bΣx2
Формулы расчета параметров уравнения парной регрессии:
a - свободный член уравнения регрессии (пересечение с осью ОУ), показывает начало отсчета. Экономически не интерпретируется.
b - показывает угол наклона линии регрессии или коэффициент регрессии. Он является мерой зависимости переменной у от переменной х. В линейном уравнении регрессии параметр b является абсолютным показателем силы связи. При степенной зависимости параметр b -это относительный показатель силы связи или коэффициент эластичности.
Условия применения МНК: 1) модель регрессии должна быть линейной по параметрам; 2) факторный признак х является заданной, а не случайной величиной; 3) значения ошибки (остатка)- случайные. Их изменение не образует определенной модели. Не должно быть взаимосвязи между фактором х и остатками (гомоскедастичность); 4) число наблюдений должно быть больше числа оцениваемых параметров (в 5-6 раз); 5) значения переменной x не должны быть одинаковыми.; 6) изучаемая совокупность должна быть однородной; 7) модель регрессии должна быть корректно специфицирована; 8) в модели не должно наблюдаться тесной взаимосвязи между факторами (это условие для множественной регрессии).
 | |||
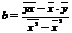 | |||
Оценка существенности уравнения в целом и отдельных его параметров ( -критерий Фишера и
-критерий Фишера и  -критерий Стьюдента).
-критерий Стьюдента).
После того как уравнение линейной регрессии построено, производится оценка значимости уравнения в целом и отдельных его параметров.
Значимость уравнения в целом оценивается по значению (величине) F–статистики Фишера. При этом выдвигается основная гипотеза  о том, что коэффициент регрессии b равен нулю и фактор X не влияет на результат Y.
о том, что коэффициент регрессии b равен нулю и фактор X не влияет на результат Y.
Для расчёта F используют дисперсии на одну степень свободы; такие дисперсии сравнимы между собой по величине, так как приведены к общей шкале.
df – число степеней свободы (degrees of freedom),
df TSS = n–1, то есть свободно могут варьироваться n–1 отклонений, а n-е отклонение может быть вычислено по этим отклонениям и среднему значению 
При заданном объёме наблюдений величина RSS в парной регрессии зависит от одной константы, а именно от коэффициента регрессии b, то есть RSS имеет одну степень свободы.


Дисперсии на одну степень свободы для парной регрессии обозначаются так:


По таблице Фишера–Снедекора, содержащей критические значения F при разных уровнях γ существенности нулевой гипотезы и разных df, найдём Fкр (критическое значение) для конкретной задачи: 

Если расчётное значение F >Fкр, то H0 отклоняется и связь между X и Y признаётся существенной, а уравнение признается адекватным. Если F < < < Fкр, то уравнение признается неадекватным.

В линейной регрессионной модели оценивают значимость не только уравнения в целом, но и отдельных его параметров. Для этого вначале определяются их стандартные ошибки: Sa, Sb, Sr.



Имея в распоряжении величины a, b, rxy и их стандартные ошибки, можно вычислить t–статистики Стьюдента для оценки значимости этих параметров.

Выдвигается гипотеза H0 о незначимости интересующего коэффициента регрессии. Если  , то гипотеза H0 не отклоняется, в противном случае она отклоняется и соответствующий коэффициент признается значимым.
, то гипотеза H0 не отклоняется, в противном случае она отклоняется и соответствующий коэффициент признается значимым.

На практике для приближенной оценки руководствуются следующим правилом:
 – параметр значимым не признается, так как доверительная вероятность < 0,7;
– параметр значимым не признается, так как доверительная вероятность < 0,7;
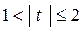 – оценка параметра относительно значима и доверительная вероятность находится в пределах 0,7
– оценка параметра относительно значима и доверительная вероятность находится в пределах 0,7 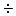 0,95;
0,95;
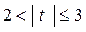 – оценка значима и доверительная вероятность находится в пределах 0,95
– оценка значима и доверительная вероятность находится в пределах 0,95 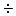 0,99;
0,99;
 – оценка гарантированно значима.
– оценка гарантированно значима.
Эти правила хорошо работают при числе наблюдений больше десяти.
Прогноз по линейному уравнению регрессии. Средняя ошибка аппроксимации.
В прогнозных расчетах по уравнению регрессии определяется предсказываемое (yp) значение как точечный прогноз  при xp = xk, т.е. путем подстановки в уравнение регрессии
при xp = xk, т.е. путем подстановки в уравнение регрессии  соответствующего значения x. Однако точечный прогноз явно не реален. Поэтому он дополняется расчетом стандартной ошибки
соответствующего значения x. Однако точечный прогноз явно не реален. Поэтому он дополняется расчетом стандартной ошибки  , т.е.
, т.е. 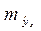 и соответственно, интервальной оценкой прогнозного значения:
и соответственно, интервальной оценкой прогнозного значения:
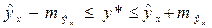
Чтобы понять, как строится формула для определения величин стандартной ошибки  , обратимся к уравнению линейной регрессии:
, обратимся к уравнению линейной регрессии:  . Подставим в это уравнение выражение параметра a:
. Подставим в это уравнение выражение параметра a:
 ,
,
тогда уравнение регрессии примет вид:
 .
.
Отсюда вытекает, что стандартная ошибка 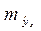 зависит от ошибки y и ошибки коэффициента регрессии b, т.е.
зависит от ошибки y и ошибки коэффициента регрессии b, т.е.
 . (1.23)
. (1.23)
Из теории выборки известно, что 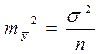 . Используя в качестве оценки s 2 остаточную дисперсию на одну степень свободы S 2, получим формулу расчета ошибки среднего значения переменной y:
. Используя в качестве оценки s 2 остаточную дисперсию на одну степень свободы S 2, получим формулу расчета ошибки среднего значения переменной y:
 . (1.24)
. (1.24)
Ошибка коэффициента регрессии, как уже было показано, определяется формулой:
 .
.
Считая, что прогнозное значение фактора xp = xk, получим следующую формулу расчета стандартной ошибки предсказываемого по линии регрессии значения, т.е. 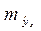 :
:
 . (1.25)
. (1.25)
Соответственно 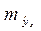 имеет выражение:
имеет выражение:
 . (1.26)
. (1.26)
Рассмотренная формула стандартной ошибки предсказываемого среднего значения y при заданном значении xk характеризует ошибку положения линии регрессии. Величина стандартной ошибки 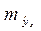 , как видно из формулы, достигает минимума при
, как видно из формулы, достигает минимума при  , и возрастает по мере того, как "удаляется" от
, и возрастает по мере того, как "удаляется" от  в любом направлении. Иными словами, чем больше разность между xk и x, тем больше ошибка
в любом направлении. Иными словами, чем больше разность между xk и x, тем больше ошибка 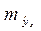 , с которой предсказывается среднее значение y для заданного значения xk. Можно ожидать наилучшие результаты прогноза, если признак-фактор x находится в центре области наблюдений x и нельзя ожидать хороших результатов прогноза при удалении xk от
, с которой предсказывается среднее значение y для заданного значения xk. Можно ожидать наилучшие результаты прогноза, если признак-фактор x находится в центре области наблюдений x и нельзя ожидать хороших результатов прогноза при удалении xk от  . Если же значение xk оказывается за пределами наблюдаемых значений x, используемых при построении линейной регрессии, то результаты прогноза ухудшаются в зависимости от того, насколько xk отклоняется от области наблюдаемых значений фактора x.
. Если же значение xk оказывается за пределами наблюдаемых значений x, используемых при построении линейной регрессии, то результаты прогноза ухудшаются в зависимости от того, насколько xk отклоняется от области наблюдаемых значений фактора x.
На графике доверительные границы для  представляют собой гиперболы, расположенные по обе стороны от линии регрессии (рис. 1.5).
представляют собой гиперболы, расположенные по обе стороны от линии регрессии (рис. 1.5).

|
Рис. 1.5 показывает, как изменяются пределы в зависимости от изменения xk: две гиперболы по обе стороны от линии регрессии определяют 95% -ые доверительные интервалы для среднего значения y при заданном значении x.
Однако фактические значения y варьируют около среднего значения  . Индивидуальные значения y могут отклоняться от
. Индивидуальные значения y могут отклоняться от  на величину случайной ошибки e, дисперсия которой оценивается как остаточная дисперсия на одну степень свободы S2. Поэтому ошибка предсказываемого индивидуального значения y должна включать не только стандартную ошибку
на величину случайной ошибки e, дисперсия которой оценивается как остаточная дисперсия на одну степень свободы S2. Поэтому ошибка предсказываемого индивидуального значения y должна включать не только стандартную ошибку  , но и случайную ошибку S.
, но и случайную ошибку S.
Средняя ошибка прогнозируемого индивидуального значения y  составит:
составит:
 . (1.27)
. (1.27)
При прогнозировании на основе уравнения регрессии следует помнить, что величина прогноза зависит не только от стандартной ошибки индивидуального значения y, но и от точности прогноза значения фактора x. Его величина может задаваться на основе анализа других моделей, исходя из конкретной ситуации, а также анализа динамики данного фактора.
Рассмотренная формула средней ошибки индивидуального значения признака y (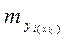 ) может быть использована также для оценки существенности различия предсказываемого значения, исходя из регрессионной модели и выдвинутой гипотезы развития событий.
) может быть использована также для оценки существенности различия предсказываемого значения, исходя из регрессионной модели и выдвинутой гипотезы развития событий.
Средняя ошибка аппроксимации - среднее отклонение расчетных значений от фактических:
, где yx - расчетное значение по уравнению.
Значение средней ошибки аппроксимации до 15% свидетельствует о хорошо подобранной модели уравнения.
Нелинейная регрессия. Классы нелинейных регрессий.
При исследовании социально-экономических явлений и процессов далеко не все зависимости можно описать с помощью линейной связи. Поэтому в эконометрическом моделировании широко используется класс нелинейных моделей регрессии, которые делятся на два класса:
1) модели регрессии, нелинейные относительно включенных в анализ независимых переменных, но линейные по оцениваемым параметрам;
2) модели регрессии, нелинейные по оцениваемым параметрам.
К моделям регрессии, нелинейным относительно включённых в анализ независимых переменных (но линейных по оцениваемым параметрам), относятся полиномы выше второго порядка и гиперболическая функция.
Модели регрессии, нелинейным относительно включённых в анализ независимых переменных, характеризуются тем, что зависимая переменная yi линейно связана с параметрами модели.
Полиномы или полиномиальные функции применяются при анализе процессов с монотонным развитием и отсутствием пределов роста. Данному условию отвечают большинство экономических показателей (например, натуральные показатели промышленного производства). Полиномиальные функции характеризуются отсутствием явной зависимости приростов факторных переменных от значений результативной переменной yi.
Общий вид полинома n -го порядка (n -ой степени):

Чаще всего в эконометрическом моделировании применяется полином второго порядка (параболическая функция), характеризующий равноускоренное развитие процесса (равноускоренный рост или снижение уровней).:

Полиномы, чей порядок выше четвёртого, в эконометрических исследованиях обычно не применяются, потому что они не способны точно отразить существующую зависимость между результативной и факторными переменными.
Гиперболическая функция характеризует нелинейную зависимость между результативной переменной yi и факторной переменной xi, однако, данная функция является линейной по оцениваемым параметрам и.
Гиперболоид или гиперболическая функция имеет вид:

Данная гиперболическая функция является равносторонней.
В качестве примера эконометрической модели в виде гиперболической функции можно привести модель зависимости затрат на единицу продукции от объёма производства.
Неизвестные параметры модели регрессии, нелинейной по факторным переменным, можно найти только после того, как модели будет приведена к линейному виду.
Для того чтобы оценить неизвестные параметры нелинейной регрессионной модели необходимо привести её к линейному виду. Суть процесс линеаризации нелинейных по факторным переменным моделей регрессии заключается в замене нелинейных факторных переменных на линейные переменные.
Рассмотрим процесс линеаризации полиномиальной функции порядка n:

Заменим все факторные переменные на линейные следующим образом:
x=c1;
x2=c2;
x3=c3;
…
xn=cn.
Тогда модель множественной регрессии можно записать в виде:
yi=
Рассмотрим процесс линеаризации гиперболической функции:

Данная функция может быть приведена к линейному виду путём замены нелинейной факторной переменной 1/x на линейную переменную с. Тогда модель регрессии можно записать в виде:
yi=
Следовательно, модели регрессии, нелинейные относительно включенных в анализ независимых переменных, но линейные по оцениваемым параметрам, могут быть преобразованы к линейному виду. Это позволяет применять к линеаризованным моделям регрессии классические методы определения неизвестных параметров модели (метод наименьших квадратов), а также методы проверки различных гипотез.
Регрессии нелинейные относительно включенных в анализ объясняющих переменных.
Регрессии нелинейные по включенным переменным сводятся к линейному виду с помощью методов линеаризации простой заменой переменных, а дальнейшая оценка параметров производится с помощью метода наименьших квадратов. Рассмотрим некоторые функции.
Полином второй степени  приводится к линейному виду с помощью замены:
приводится к линейному виду с помощью замены:  . В результате приходим к двухфакторному уравнению
. В результате приходим к двухфакторному уравнению  , оценка параметров которого при помощи МНК, приводит к системе следующих нормальных уравнений:
, оценка параметров которого при помощи МНК, приводит к системе следующих нормальных уравнений:

А после обратной замены переменных получим

Полином второй степени обычно применяется в случаях, когда для определенного интервала значений фактора меняется характер связи рассматриваемых признаков: прямая связь меняется на обратную или обратная на прямую.
Аналогично, для полинома третьего порядка получим трёхфакторную модель.
Для полинома степени m, получим множественную регрессию с m объясняющими переменными
 .
.
Среди нелинейной полиномиальной модели чаще всего используется полином второй степени, реже – третьей.
Для равносторонней гиперболы  замена
замена  приводит к уравнению парной линейной регрессии
приводит к уравнению парной линейной регрессии  , для оценки параметров которого используется МНК. Система линейных уравнений при применении МНК будет выглядеть следующим образом:
, для оценки параметров которого используется МНК. Система линейных уравнений при применении МНК будет выглядеть следующим образом:

Такая модель может быть использована для характеристики связи удельных расходов сырья, материалов, топлива от объема выпускаемой продукции, времени обращения товаров от величины товарооборота, процента прироста заработной платы от уровня безработицы (например, кривая А.В. Филлипса), расходов на непродовольственные товары от доходов или общей суммы расходов (например, кривые Э. Энгеля) и в других случаях.
Аналогичным образом приводятся к линейному виду зависимости 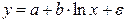 ,
,  и другие.
и другие.
Регрессии нелинейные по оцениваемым параметрам.
Регрессии, нелинейными по оцениваемым параметрам, делятся на два типа: нелинейные модели внутренне линейные (приводятся к линейному виду с помощью соответствующих преобразований, например, логарифмированием) и нелинейные модели внутренне нелинейные (к линейному виду не приводятся).
К внутренне линейным моделям относятся, например, степенная функция –  , показательная –
, показательная –  , экспоненциальная –
, экспоненциальная –  , логистическая –
, логистическая –  , обратная –
, обратная –  .
.
Коэффициенты эластичности для разных видов регрессионных моделей.
Линейная y = a + bx + , y′ = b, Э =
, y′ = b, Э =  .2. Парабола 2 порядка y = a +bx + c
.2. Парабола 2 порядка y = a +bx + c  +
+  , y′ = b + 2cx, Э =
, y′ = b + 2cx, Э =  .3. Гипербола y = a+b/x +
.3. Гипербола y = a+b/x +  , y′=-b/
, y′=-b/ 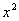 , Э =
, Э =  .4. Показательная y=a
.4. Показательная y=a  , y′ = ln
, y′ = ln  , Э = x ln b.5. Степенная y = a
, Э = x ln b.5. Степенная y = a 
 , y′ =
, y′ =  , Э = b.6. Полулогарифмическая y = a + b ln x +ε, y′ = b/x, Э =
, Э = b.6. Полулогарифмическая y = a + b ln x +ε, y′ = b/x, Э = 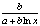 .7. Логистическая
.7. Логистическая  , y′ =
, y′ =  , Э =
, Э =  .8. Обратная y =
.8. Обратная y =  , y′ =
, y′ =  , Э =
, Э =  .
.
Корреляция и  -критерий Фишера для нелинейной регрессии.
-критерий Фишера для нелинейной регрессии.
Уравнение нелинейной регрессии, так же как и в линейной зависимости, дополняется показателями корреляции:
 = 1-
= 1-  ;
;  .
.
Величину R2 для нелинейных связей называют индексом детерминации, а R – индексом корреляции. Чем ближе значение R2 к 1, тем связь рассматриваемых признаков теснее, тем более надежно уравнение регрессии.
Если после преобразования уравнение регрессии (нелинейное по объясняющим переменным) принимает форму линейного парного уравнения регрессии, то для оценки тесноты связи может быть использован линейный коэффициент корреляции R yx = ryz, где z – преобразованная величина признака-фактора, например z = 1/ x или z = ln x.
Если преобразования в линейную форму связаны с результативным признаком (нелинейность по параметрам), то линейный коэффициент корреляции по преобразованным значениям признаков дает лишь приближенную оценку тесноты связи. Он численно не совпадает с R, R  r, так как r рассчитывается между ln y и ln x, а коэффициент детерминации использует суммы квадратов отклонений признака y, а не его логарифма.
r, так как r рассчитывается между ln y и ln x, а коэффициент детерминации использует суммы квадратов отклонений признака y, а не его логарифма.
R2 для нелинейной регрессии имеет тот же смысл, что и коэффициент детерминации.
Оценка существенности индекса корреляции производится так же, как и оценка надежности коэффициента корреляции. Индекс корреляции R используется для проверки существенности уравнения нелинейной регрессии в целом по F – критерию Фишера:
F =  , где n – число наблюдений, р – число параметров при х.
, где n – число наблюдений, р – число параметров при х.
Индекс детерминации R2 можно сравнивать с коэффициентом детерминации r 2 для обоснования возможности применения линейной функции. Чем больше кривизна линии регрессии, тем величина коэффициента детерминации r 2 меньше индекса детерминации R2. Близость этих показателей означает, что нет необходимости усложнять форму уравнения регрессии и можно использовать линейную функцию. Практически, если величина (R2 – r 2)  0,1, то предположение о линейной форме связи считается оправданным. В противном случае проводится оценка существенности различий R2, вычисленных по одним и тем же исходным данным, через t – критерий Стьюдента:
0,1, то предположение о линейной форме связи считается оправданным. В противном случае проводится оценка существенности различий R2, вычисленных по одним и тем же исходным данным, через t – критерий Стьюдента:
 ,
,
где  - ошибка разности между R2 и r 2.
- ошибка разности между R2 и r 2.
Если tнабл > tкр, то различия между рассматриваемыми показателями корреляции существенны и замена нелинейной регрессии уравнением линейной функции невозможно. Если t < 2, то различия между R и r несущественны, и, следовательно, возможно применение линейной регрессии, даже если есть предположение о некоторой нелинейности рассматриваемых соотношений признаков фактора и результата.
Если R2 и r 2 приблизительно равны, используют стандартную процедуру, известную под названием теста Бокса-Кокса. Тест включает следующие шаги:
1) определяется среднее геометрическое y в выборке;
2) пересчитываются наблюдения 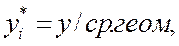 где
где  - пересчитанные значения для i-го наблюдения;
- пересчитанные значения для i-го наблюдения;
3) оценивается регрессия для  вместо y и для логарифмической модели ln y * вместо ln y;
вместо y и для логарифмической модели ln y * вместо ln y;
4) определяют величину  , где z – отношение значений суммы квадратов отклонений в пересчитанных регрессиях, n – число наблюдений.
, где z – отношение значений суммы квадратов отклонений в пересчитанных регрессиях, n – число наблюдений.
Эта статистика имеет распределение  с 1-й степенью свободы. Если
с 1-й степенью свободы. Если  <
<  кр(1,
кр(1, 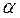 ), то разница значима. Модель с меньшей суммой квадратов отклонений обеспечивает лучшее соответствие.
), то разница значима. Модель с меньшей суммой квадратов отклонений обеспечивает лучшее соответствие.
Отбор факторов при построении уравнения множественной регрессии.
Факторы, включаемые во множественную регрессию, должны отвечать следующим требованиям.
1. Они должны быть количественно измеримы. Если необходимо включить в модель качественный фактор, не имеющий количественного измерения, то ему нужно придать количественную определенность.
2. Факторы не должны быть интеркоррелированы (т.е. между объясняющими переменными присутствует корреляция) и тем более находиться в точной функциональной связи.
Включение в модель факторов с высокой интеркорреляцией может привести к ненадежной оценке коэффициентов регрессии, так как нельзя определить их изолированное влияние на результативный показатель и параметры уравнения регрессии оказываются неинтерпретируемыми.
Включаемые во множественную регрессию факторы должны объяснить вариацию независимой переменной. Если строится модель с набором р факторов, то для нее рассчитывается показатель детерминации R2,который фиксирует долю объясненной вариации результативного признака за счет рассматриваемых в регрессии р факторов. Влияние других, не учтенных в модели факторов, оценивается как (1–R2) ссоответствующей остаточной дисперсией S2
При дополнительном включении в регрессию р+1 фактора коэффициент детерминации должен возрастать, а остаточная дисперсия уменьшаться.
Если же этого не происходит и данные показатели практически мало отличаются друг от друга, то включаемый в анализ фактор хp+1 не улучшает модель и практически является лишним фактором.
Насыщение модели лишними факторами не только не снижает величину остаточной дисперсии и не увеличивает показатель детерминации, но и приводит к статистической незначимости параметров регрессии по t-критерию Стьюдента.
Отбор факторов обычно осуществляется в две стадии: на первой подби