Тюрин Ю.И., Ларионов В.В., Чернов И.П. Физика: Сборник задач (с решениями). Часть 3. Оптика. Атомная и ядерная физика: Учебное пособие. - Томск: Изд-во Том. ун-та, 2005. – 256 с.
1. ГЕОМЕТРИЧЕСКАЯ ОПТИКА
1.1.1. Вывести с помощью принципа Ферма законы отражения и преломления света на плоской границе раздела.
1.1.2. Показать, что луч света, последовательно отразившийся от трех взаимно перпендикулярных плоских зеркал, изменит свое направление на прямо противоположное.
1.1.3. Построить изображение предмета АВ, лежащего на главной оптической оси: а) собирающей линзы; б) рассеивающей линзы.
1.1.4. Найти построением ход луча за собирающей и рассеивающей тонкими линзами (см. рисунок, где ОО’ – оптическая ось; F и F’ – передний и задний фокусы).
1.1.5. Пучок параллельных световых лучей падает из воздуха на толстую стеклянную пластину под углом 60 ° и, преломляясь, переходит в стекло. Ширина пучка в воздухе 10 см. Определите ширину пучка в стекле. Показатель преломления стекла 1,51.
Ответ: 16 см.
1.1.6. На плоскопараллельную прозрачную для света пластину толщиной 2 см падает луч под углом 60 °. Определите угол преломления этого луча, если при выходе из пластины луч смещается на 1 см.
Ответ: 36 °.
1.1.7. Точечный источник света расположен в воде на глубине 1 м. Показатель преломления воды равен 1,33. Каков радиус круга на поверхности воды, в пределах которого возможен выход лучей в воздух?
Ответ: 1,14 м.
1.1.8. Имеются две оптические среды с плоской границей раздела. Пусть q1пр – предельный угол падения луча, а q1 – угол падения, при котором преломленный луч перпендикулярен отраженному (луч идет из оптически более плотной среды). Найти относительный показатель преломления этих сред, если sin q1пр/sinq1 = h = 1,28.
Ответ: 
1.1.9. На дне ручья лежит камешек. Мальчик хочет толкнуть его палкой. Прицеливаясь, мальчик держит палку по лучу зрения под углом 45 ° к горизонту. На каком расстоянии от камешка воткнется палка в дно ручья, если его глубина 0,4 м? Где будет находиться кажущееся положение камешка, если на него смотреть сверху по вертикали? Показатель преломления воды n = 1,33.
Ответ: 15 см, h = 30 см.
1.1.10. Луч света распространяется в среде, показатель преломления которой убывает с высотой по закону n = n 0 – ky, где n 0, k – постоянные. На какой высоте луч повернет обратно. В точке у = 0 угол между направлением луча и координатой у равен a0.
Ответ: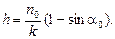 
1.1.11. Показатель преломления атмосферы планеты уменьшается с высотой h над ее поверхностью по закону n = n 0 – a h при h > n / a. Радиус планеты R. Найдите, на какой высоте над поверхностью планеты луч, испущенный горизонтально, будет обходить планету, оставаясь все время на этой высоте.
Ответ: 
.
1.1.12. Имеются две тонкие симметричные линзы: одна собирающая с показателем преломления n 1 = 1,70, другая рассеивающая с n 2 = 1,51. Обе линзы имеют одинаковый радиус кривизны поверхностей R = 10 см. Линзы сложили вплотную и погрузили в воду. Каково фокусное расстояние этой системы в воде?
Ответ: F = n 0 R / 2(n 1 – n 2) = 35 см,
где n 0 – показатель преломления воды.
1.1.13. Найти фокусное расстояние зеркала, представляющего собой тонкую симметричную двояковыпуклую стеклянную линзу с посеребренной одной поверхностью. Радиус кривизны поверхностей линзы R = 40 см.
Ответ: F = R / 2(2 n – 1) = 10 см.
1.1.14. Для некоторой стеклянной призмы угол наименьшего отклонения луча равен преломляющему углу призмы. Найти последний.
Ответ: q = 83 °.
1.1.15. В стекле с показателем преломления 1,52 имеется сферическая полость радиусом 3 см, заполненная водой с показателем преломления 1,33. На полость падают параллельные лучи света. Определите радиус светового пучка, который проникает в полость.
Ответ: 2,625 см.
1.1.16. Столб вбит в дно реки и возвышается над водой на 1 м. Найти длину тени столба на дне реки, если высота Солнца над горизонтом 30 ° (угол между солнечным лучом и поверхностью воды), глубина реки 2 м, показатель преломления воды 1,33.
Ответ: 3,45 м.
1.1.17. Каким должен быть внешний радиус изгиба световода, сделанного из прозрачного вещества с показателем преломления n, чтобы при диаметре световода, равном l, свет, вошедший в световод перпендикулярно плоскости его поперечного сечения, распространяется, не выходя через боковую поверхность наружу?
Ответ: R = l × n / (n – 1).
1.1.18. Действительное изображение предмета в вогнутом зеркале превышает по своим размерам предмет в три раза. После того как предмет отодвинули от зеркала на 80 см, его изображение стало в два раза меньше предмета. Найти фокусное расстояние зеркала.
Ответ: F = 48 см.
1.1.19. Какие очки вы пропишете близорукому человеку, который может читать текст, расположенный от глаз не далее 20 см, а какие дальнозоркому, который может читать текст, расположенный от глаз не ближе 50 см?
Ответ: D 1 = –5 дптр, D 2 = 2 дптр.
1.1.20. Каково наименьшее возможное расстояние l между предметом и его действительным изображением, создаваемым собирающей линзой с главным фокусным расстоянием F = 12 см?
Ответ: 48 см.
1.1.21. Линза, расположенная на оптической скамье между лампочкой и экраном, дает на экране резко увеличенное изображение лампочки. Когда лампочку передвинули D l = 40 см ближе к экрану, на нем появилось резко уменьшенное изображение лампочки. Определить фокусное расстояние f, если расстояние l от лампочки до экрана равно 80 см.
Ответ: 15 см.
1.1.22. При некотором положении предмета лупа дала четырехкратное увеличение. Как изменится это число, если расстояние от предмета до лупы уменьшить в 1,5 раза?
Ответ: Уменьшится в 2 раза.
1.1.23. Найти увеличение зрительной трубы кеплеровского типа, установленной на бесконечность, если D – диаметр оправы ее объектива, а d – диаметр изображения этой оправы, образуемого окуляром трубы.
Ответ: Г = D / d.
1.1.24. Найти коэффициент увеличения изображения предмета АВ, даваемого тонкой рассеивающей линзой с фокусным расстоянием F.
Ответ: Г = 0,17.
1.1.25. Вычислить оптическую силу и фокусные расстояния тонкой симметричной двояковыпуклой стеклянной линзы, с одной стороны которой находится воздух, а с другой – вода, если оптическая сила этой линзы в воздухе D 0 = +10 дптр.
Ответ: 
дптр; F = 15 см; F ¢ = 20 см.
Здесь n 0, n – показатели преломления воды и стекла.
1.2.1. Система, состоящая из трех тонких линз (см. рисунок), находится в воздухе. Оптическая сила каждой линзы 10,0 дптр. Определить: а) положение точки схождения параллельного пучка, падающего слева, после прохождения через систему; б) расстояние от первой линзы до точки на оси слева от системы, при котором эта точка и ее изображение будут расположены симметрично относительно системы.
Ответ: а) Справа от последней линзы на 3 см от нее; б) l = 17 см.
1.2.2. В центре сферического зеркала расположен точечный источник света S. Зеркало разрезали пополам. Обе половины симметрично отодвинули на расстояние h от главной оптической оси целого зеркала. Найти расстояние между изображениями источника света в зеркалах.
Ответ: 4 h.
1.2.3. Улитка размером а сидит на дальней стенке прямоугольного аквариума ширины l. Во сколько раз изменится видимый угловой размер улитки, если из аквариума слить воду? Наблюдатель расположился на расстоянии L от аквариума.
Ответ: Уменьшится в (L + l) / (L + nl) раз.
1.2.4. Открытый сверху сосуд, на дне которого находится точечный монохроматический источник света, заполняют снизу водой так, что ее уровень поднимается со скоростью v = 9,0 мм/с. Найти относительный сдвиг частоты Dw / w света, который наблюдают над поверхностью воды вдоль вертикали, проходящей через источник. Наблюдатель предполагается неподвижным.
Ответ: Dw / w = (n – 1) v / c = 1×10–11.
1.2.5. При каком минимальном угле падения луча света на стопку плоских прозрачных пластин, показатель преломления каждой из которых в k раз меньше, чем у вышележащей, луч не пройдет сквозь стопку? Показатель преломления верхней пластины n, число пластин N.
Ответ: sin a = n / k N – 1.
1.2.6. На дне стеклянной ванны лежит зеркало, поверх которого налит слой воды высотой 20 см. В воздухе на высоте 30 см над поверхностью воды висит лампа. На каком расстоянии от поверхности воды смотрящий в воду наблюдатель будет видеть изображение лампы в зеркале? Показатель преломления воды 1,33.
Ответ: 60 см.
1.2.7. В днище судна сделан стеклянный иллюминатор для наблюдения за морскими животными. Диаметр иллюминатора 40 см, много меньше толщины стекла. Определите площадь обзора дна из такого иллюминатора. Показатель преломления морской воды 1,4, расстояние до дна 5 м.
Ответ: 82 м2.
1.2.8. Внутри стеклянного шара радиусом r = 0,1 м слева от его центра вблизи поверхности находится точечный источник света S. На каком расстоянии справа от центра шара радиус светового пучка, вышедший из шара, будет равен r? Показатель преломления стекла n = 2.
Ответ: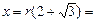 
0,37 м.
1.2.9. Человек движется вдоль главной оптической оси объектива фотоаппарата со скоростью v = 5 м/с. С какой скоростью u необходимо перемещать матовое стекло фотоаппарата, чтобы изображение человека на нем все время оставалось резким. Главное фокусное расстояние F объектива равно 20 см. Вычисления выполнить для случая, когда человек находился на расстоянии d = 10 м от фотоаппарата.
Ответ: 2,08 мм/с.
1.2.10. Фотографируется момент погружения в воду прыгуна с вышки высотой 4,9 м. Фотограф находится у воды на расстоянии 10 м от места погружения. Фокусное расстояние объектива фотоаппарата равно 20 см. На негативе допустимо «размытие» изображения не более 0,05 мм. На какое наибольшее время (в миллисекундах) должен быть открыт затвор фотоаппарата?
Ответ: 0,25 мс.
1.2.11. Оптическая система состоит из двух собирающих линз с фокусными расстояниями 20 и 10 см. Расстояние между линзами 30 см. Предмет находится на расстоянии 30 см от первой линзы. Определите, на каком расстоянии от второй линзы находится изображение предмета?
Ответ: 7,5 см.
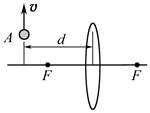1.2.12. Точка А движется с постоянной скоростью 2 см/с в направлении, как показано на рисунке. С какой скоростью движется изображение этой точки, если d = 0,15 м, а фокусное расстояние линзы F = 0,1 м?
Ответ: 4 см/с.
1.2.13. Источник света находится на l = 90 см от экрана. Тонкая собирающая линза, помещенная между источником света и экраном, дает четкое изображение источника при двух ее положениях. Найти фокусное расстояние линзы, если а) расстояние между обоими положениями D l = 30 см; б) поперечные размеры изображения при одном положении линзы в h = 4,0 раза больше, чем при другом.
Ответ: а) F = (l 2 – D l 2) / 4 l = 20 см;
б) 
= 20 см.
1.2.14. Линзу с фокусным расстоянием F и радиусами кривизны r 1 и r 2 встроили в стенку аквариума так, что поверхность линзы с радиусом кривизны r 2 находится внутри аквариума. Показатель преломления воды n. Определите, на каком расстоянии от линзы сфокусируется параллельный пучок света: а) входящий в аквариум; б) выходящий из аквариума.
Ответ: а) 
б) 
1.2.15. Точечный источник света помещен на главной оптической оси собирающей линзы L 1 с фокусным расстоянием 20 см на расстоянии 40 см от этой линзы. По другую сторону линзы L 1 в ее фокальной плоскости помещена рассеивающая линза L 2 так, что вышедшие из линзы L 2 лучи кажутся исходящими из самого источника. Определите фокусное расстояние рассеивающей линзы.
Ответ: F = –15 см.
1.2.16. С помощью фотоаппарата с объективом, оптическая сила которого D = 10 дптр, фотографируют предмет, находящийся на дне водоема глубиной h 1 = 1,2 м. Каково расстояние между объективом и пленкой? Объектив расположен на расстоянии h 2 = 0,50 м от поверхности воды.
Ответ: 
= 11 см.
1.2.17. В трубку вставлены две двояковыпуклые линзы таким образом, что их главные оптические оси совпадают. Расстояние между линзами l = 16 см. Главное фокусное расстояние первой линзы F 1 = 8 см, второй – F 2 = 5 см. Предмет высотой h = 9 см помещен на расстоянии d 1 = 40 см от первой линзы. На каком расстоянии от второй линзы получилось изображение? Какова высота h ¢?
Ответ: На расстоянии 30 см; h ¢ = 11,25 см.
1.2.18. Лупа дает увеличение Г1 = 2. Вплотную к ней приложили собирательную линзу с оптической силой D = 20 дптр. Какое увеличение Г2 будет давать такая составная лупа?
Ответ: Г2 = 7.
1.2.19. При окуляре с фокусным расстоянием F 2 = 50 мм телескоп дает угловое увеличение Г1 = 60. Какое угловое увеличение Г2 даст один объектив, если убрать окуляр и рассматривать действительное изображение, созданное объективом, невооруженным глазом с расстояния наилучшего зрения?
Ответ: Г = 12.
1.2.20. Телескоп наведен на Солнце. Фокусное расстояние F 1 объектива телескопа равно 3 м. Окуляр с фокусным расстоянием F 2 = 50 мм проецирует действительное изображение Солнца, созданное объективом на экран, расположенный на расстоянии b = 60 см от окуляра. Плоскость экрана перпендикулярна оптической оси телескопа. Определить линейный диаметр d изображения Солнца на экране, если диаметр Солнца на небе виден невооруженным глазом под углом a = 32 ¢.
Ответ: 30,7 см.
1.2.21. Фокусное расстояние F 1 объектива телескопа равно 1 м. В телескоп рассматривали здание, находящееся на расстоянии d = 1 км. В каком направлении и на сколько нужно передвинуть окуляр, чтобы получить резкое изображение в двух случаях: 1) если после здания будут рассматривать Луну; 2) если вместо Луны будут рассматривать близкие предметы, находящиеся на расстоянии d 1 = 100 м?
Ответ: 1) К объективу на 1 мм; 2) от объектива на 9 мм.
1.2.22. Галилеева труба 10-кратного увеличения при установке на бесконечность имеет длину 45 см. Найти: а) фокусные расстояния объектива и окуляра трубы; б) на какое расстояние надо передвинуть окуляр трубы, чтобы ясно видеть предметы на расстоянии 50 м.
Ответ: а) 50 см и 5 см; б) отодвинуть на 0,5 см.
1.2.23. Оптическая сила D объектива телескопа равна 0,5 дптр. Окуляр действует, как лупа, дающая увеличение Г1 = 10. Какое увеличение Г2 дает телескоп?
Ответ: Г2 = 80.
1.2.24. Расстояние d между фокусами объектива и окуляра внутри микроскопа равно 16 см. Фокусное расстояние F 1 объектива равно 1 мм. С каким фокусным расстоянием F 2 следует взять окуляр, чтобы получить увеличение Г = 500?
Ответ: F 2 = 2 см.
1.2.25. Микроскоп имеет длину 20 см. Фокусные расстояния объектива и окуляра соответственно равны 0,40 и 2,0 см. На каком расстоянии от объектива надо поместить предмет, чтобы его отчетливо видеть человеку с нормальным зрением?
Ответ: 4,1 мм.
ИНТЕРФЕРЕНЦИЯ СВЕТА
2.1.1. Во сколько раз N в опыте Юнга нужно изменить расстояние до экрана, чтобы пятая светлая полоса новой интерференционной картины оказалась на том же расстоянии, что и третья в прежней картине? То же для третьей и седьмой темных полос.
Ответ: 0,6; 15/7.
2.1.2. В опыте Юнга расстояние между щелями d = 0,5 мм, длина волны l = 550 нм. Найти расстояние L от щелей до экрана, если расстояние между соседними полосами D х = 1 мм.
Ответ: L = 91 см.
2.1.3. Найти длину волны l монохроматического излучения, если в опыте Юнга расстояние первого интерференционного максимума от центрального максимума х = 0,05 см, расстояние от щелей до экрана L = 5 м, расстояние между щелями d = 0,5 см.
Ответ: l = 500 нм.
2.1.4. Во сколько раз N увеличится расстояние между соседними интерференционными полосами на экране в опыте Юнга, если зеленый (l1 = 5×10–5 см) светофильтр заменить красным (l2 = 6,5×10–5 см)?
Ответ: N = 1,3.
2.1.5. В опыте с зеркалами Френеля расстояние между мнимыми изображениями источника света d = 0,5 мм, расстояние до экрана L = 5 м. В зеленом свете получились интерференционные полосы на расстоянии D х = 5 мм друг от друга. Найти длину волны l зеленого света.
Ответ: l = 500 нм.
2.1.6. На рисунке изображена принципиальная интерференционная схема с двумя светящимися щелями. Оценить максимальную ширину b max щелей, при которой интерференционные полосы будут еще различимы достаточно отчетливо, считая свет строго монохроматичным.
Ответ: b max = D х /4.
2.1.7. Плоская световая волна падает на бизеркала Френеля, угол между которыми a = 2¢. Найти длину волны света l, если ширина интерференционной полосы на экране D х = 0,55 мм.
Ответ: l = 2a D х = 640 нм.
2.1.8. Расстояния от призмы Френеля с показателем преломления n = 1,5 до узкой щели и экрана равны соответственно а = 25 и b = 100 см. Преломляющий угол призмы Q = 20¢. Найти длину волны света l, если ширина интерференционной полосы на экране D х = 0,55 мм.
Ответ: 
640 нм.
2.1.9. В изображенной на рисунке установке с бизеркалами Френеля S – источник света в виде перпендикулярной к плоскости рисунка щели; Э – экран. Расстояние r = 0,1 м, b = 1 м. Найти: а) значение угла a, при котором для l = 500 нм ширина D х интерференционных полос на экране будет равна 1 мм; б) максимальное N число полос, которое можно наблюдать в этом случае.
Ответ: а) a = 9,5¢; б) N = 5.
2.1.10. Выразить расстояние х от центра интерференционной картины до m -й светлой полосы в опыте с бипризмой (см. рисунок). Показатель преломления призмы n, преломляющий угол q, длина волны l. Интерферирующие лучи падают на экран приблизительно перпендикулярно.
Ответ: 
2.1.11. В схеме, предложенной Ллойдом, световая волна, падающая на экран Э непосредственно от светящейся щели S, интерферирует с волной, отразившейся от зеркала З (см. рисунок). Пусть расстояние от щели до плоскости зеркала h = 1 мм, расстояние от щели до экрана L = 1 м, длина световой волны l = 500 нм. Найти: а) ширину интерференционных полос D х; б) при какой минимальной ширине щели b min интерференционная картина на экране полностью исчезает.
Ответ: а) D х = 0,25 мм; б) b min = 0,25 мм.
2.1.12. Рассеянный монохроматический свет с длиной волны l = 0,6 мкм падает на пленку толщиной d = 15 мкм с показателем преломления n = 1,5. Определить угловое расстояние между соседними максимумами, наблюдаемыми в отраженном свете под углами с нормалью, близкими к 45 °.
Ответ: Dj = 3°.
2.1.13. В опыте Ллойда в качестве отражающей взята поверхность стеклянной пластины, а источником света служит параллельная щель, середина которой находится на расстоянии h = 1 мм от продолжения отражающей поверхности. Экран расположен на расстоянии L = 4 м от щели, длина волны l = 700 нм. Найти число интерференционных полос n, укладывающихся на отрезке экрана длиной l = 4,2 мм.
Ответ: 
2.1.14. Установка для получения колец Ньютона освещается монохроматическим светом. Наблюдение ведется в отраженном свете. Радиусы двух соседних темных колец равны соответственно r К = 4,0 мм и rК +1 = 4,38 мм. Радиус кривизны линзы равен R = 6,4 м. Найти порядковые номера колец и длину волны l падающего света.
Ответ: К = 5; l = 500 нм.
2.1.15. Установка для наблюдения колец Ньютона освещена монохроматическим светом с длиной волны l = 0,6 мкм, падающим нормально. Найти толщину воздушного слоя h между линзой и стеклянной пластиной в том месте, где наблюдается четвертое темное кольцо в отраженном свете.
Ответ: h = 1,2 мкм.
2.1.16. Найти расстояние l между десятым и одиннадцатым кольцами Ньютона, наблюдаемыми в отраженном свете, если расстояние между вторым и третьим l 1 = 3 мм. Свет падает нормально.
Ответ: l = 0,15 мм.
2.1.17. Диаметр четвертого темного кольца Ньютона в отраженном свете d = 9 мм. Радиус кривизны линзы R = 8,6 м. Монохроматический свет падает нормально. Найти длину волны l падающего света.
Ответ: l = 590 нм.
2.1.18. Найти радиус кривизны R линзы, применяемой для наблюдения колец Ньютона, если расстояние между вторым и третьим светлыми кольцами l = 0,50 мм. Освещение производится монохроматическим светом с длиной волны l = 550 нм. Наблюдение ведется в отраженном свете.
Ответ: R = 3,6 м.
2.1.19. Плосковыпуклая стеклянная линза, радиус кривизны которой R = 40 см, соприкасается выпуклой поверхностью со стеклянной пластинкой. При этом в отраженном свете радиус некоторого кольца r = 2,5 мм. Наблюдая за кольцом, линзу осторожно отодвинули от пластинки на D h = 5,0 мкм. Каким стал радиус r ¢ этого кольца?
Ответ: 
мм.
2.1.20. Плосковыпуклая стеклянная линза с радиусом кривизны сферической поверхности R = 12,5 см прижата к стеклянной пластинке. Диаметр некоторого темного кольца Ньютона в отраженном свете d 1 = 1,0 мм, диаметр же темного кольца, порядковый номер которого на 5 единиц больше, d 2 = 1,5 мм. Определить длину волны света l.
Ответ: r 4 = 2 мм; r 9 = 3 мм.
2.1.21. Найти расстояние l между двадцатым и двадцать первым светлыми кольцами Ньютона, если расстояние между вторым и третьим l 1 = 1 мм, а кольца наблюдаются в отраженном свете.
Ответ: D l = 0,32 мм.
2.1.22. Кольца Ньютона наблюдаются в отраженном свете длиной волны l = 589 нм. Расстояние между первым и вторым светлыми кольцами l = 0,5 мм. Найти радиус кривизны R плосковыпуклой линзы.
Ответ: R = 1,6 мм.
2.1.23. Расстояние между пятым и двадцать пятым светлыми кольцами Ньютона l = 9 мм. Радиус кривизны линзы R = 15 м. Наблюдение колец ведется в отраженном свете. Найти длину волны l монохроматического света, падающего нормально на установку.
Ответ: l = 675 нм.
2.1.24. На тонкую пленку (n = 1,33) падает параллельный пучок белого света. Угол падения a = 52 °. При какой минимальной толщине пленки отраженный свет наиболее сильно окрашен в желтый цвет (l = 0,60 мкм)?
Ответ: 0,14 мкм.
2.1.25. Пучок белого света падает нормально на стеклянную пластинку, толщина которой d = 0,4 мкм. Показатель преломления стекла n = 1,5. Какие длины волн l, лежащие в пределах видимого спектра (от 4×10–7 до 7×10–7 м), усиливаются в отраженном пучке?
Ответ: l = 4,8×10–7 м.
2.1.26. Найти преломляющий угол q стеклянного клина, если на него нормально падает монохроматический свет, длина волны которого l = 0,52 мкм и число интерференционных полос, приходящихся на 1 см, равно 8. Показатель преломления стекла для указанной длины волны n = 1,49.
Ответ: q = 25².
2.1.27. Свет с длиной волны l = 0,55 мкм от удаленного точечного источника падает нормально на поверхность стеклянного клина. Систему интерференционных полос наблюдают в отраженном свете, расстояние между соседними максимумами на поверхности клина 0,21 мм. Найти угол q между гранями клина.
Ответ: q = 3¢.
2.1.28. Свет с длиной волны l = 600 нм падает на тонкую мыльную пленку под углом a = 30 °. В отраженном свете на пленке наблюдаются интерференционные полосы. Расстояние между соседними полосами D х = 4,0 мм. Показатель преломления мыльной пленки n = 1,33. Найти угол q между поверхностями пленки.
Ответ: 
2.1.29. Мыльная пленка освещается излучением следующего спектрального состава: l1 = 410,2 нм, l2 = 434 нм, l3 = 486,1 нм, l4 = 656,3 нм. Наблюдение ведется в отраженном сете. Какие световые волны l будут максимально усилены и какие максимально ослаблены в результате интерференции при толщине пленки d = 0,615 мкм? Свет падает перпендикулярно к поверхности пленки. Показатель преломления мыльной жидкости n = 1,33.
Ответ: Усилена l = 656 нм; ослаблена l = 410 нм.
2.1.30. Для уменьшения потерь света при отражении от стекла на поверхность объектива (n 1 = 1,7) нанесена тонкая прозрачная пленка (n = 1,3). При какой наименьшей ее толщине d min произойдет максимальное ослабление отраженного света, длина волны которого приходится на среднюю часть видимого спектра (l0 = 560 нм)? Считать, что лучи падают нормально к поверхности объектива.
Ответ: d min = 0,11 мкм.
2.2.1. В опыте Юнга отверстия освещались монохроматическим светом длиной волны l = 6×10–5 см; расстояние между отверстиями d = 1 мм и расстояние от отверстий до экрана L = 3 м. Найти расстояние xi трех первых максимумов от нулевого максимума.
Ответ: х 1 = 1,8 мм; х 2 = 3,6 мм; х 3 = 5,4 мм.
2.2.2. В опыте Юнга экран был удален от отверстий на расстояние 5 м. Расстояние между отверстиями 0,5 см, расстояние от третьего интерференционного максимума до центральной полосы 0,15 см. Определите: а) длину волны монохроматического света; б) расстояние между соседними светлыми интерференционными полосами; в) какова будет картина на экране, если его освещать белым светом?
Ответ: а) 0,5 мкм; б) 0,5 мм.
2.2.3. Расстояние между двумя мнимыми изображениями источника света в зеркалах Френеля d = 0,7 мм, расстояние от изображений до экрана l = 2,267 м, ширина полосы интерференции х = 1,9 мм, расстояние от источника до линии пересечения зеркал r = 10 см. Определите: а) длину волны монохроматического света, падающего на зеркала, острый угол между ними и число полос на экране; б) закон распределения интенсивности света на экране; в) допустимые размеры точечного источника, при которых можно наблюдать отчетливую картину интерференции.
Ответ: а) 0,585 мкм; a = 0,035; N = 1200;
б) 
в) d = 0,95 мм.
2.2.4. Тупой угол стеклянной бипризмы Френеля (n = 1,5) равен 179°, длина волны источника света 0,60 мкм, расстояние от источника света до призмы 8 см, до экрана – 5 м. Определите расстояние между соседними интерференционными полосами D х и число N полос интерференции.
Ответ: D х = 0,43 мм; N = 10.
2.2.5. В опыте Ллойда по интерференции в качестве отражателя света используется поверхность стеклянной пластинки П, а источником света служит параллельная ей светящаяся щель. Середина щели находится на расстоянии d = 1 мм от продолжения отражающей поверхности, экран Э удален от щели на расстояние l = 4 м, длина волны l = 0,7 мкм. На каком расстоянии х от середины центральной полосы находится третья светлая полоса? Какую ширину должна иметь щель, чтобы полосы были достаточно четкими?
Ответ: х = 4,9 мм; d = 0,7 мм.
2.2.6. Рассеянный монохроматический свет с длиной волны 0,60 мкм падает на пленку толщиной 15 мкм с показателем преломления 1,5. Определите угловое расстояние между соседними максимумами, наблюдаемыми в отраженном свете под углами с нормалью, близкими к 45°.
Ответ: 3°.
2.2.7. Интерференция при отражении света наблюдается в тонком стеклянном клине. Расстояние между соседними темными полосами 5 мм, показатель преломления стекла 1,5, длина световой волны 0,58 мкм. Определите угол между гранями клина.
Ответ: 8 ².
2.2.8. Две плоскопараллельные стеклянные пластинки приложены одна к другой так, что между ними образовался воздушный клин с острым углом 30². На одну из пластинок падает нормально монохроматический свет с длиной волны 0,6 мкм. На каком расстоянии от линии соприкосновения пластинок наблюдаются первая и вторая светлые полосы в отраженном свете?
Ответ: 3,1; 5,2 мм.
2.2.9. Полосы равной толщины наблюдаются в воздушном пространстве между двумя плоскопараллельными стеклянными пластинками, образующими малый угол. Клин освещается рассеянным монохроматическим светом. Пластинки рассматривают с расстояния наилучшего зрения (25 см) в направлении, перпендикулярном к поверхности клина, причем глаз может смещаться перпендикулярно к ребру клина. Оцените максимальное число интерференционных полос, которые можно видеть при диаметре зрачка глаза 5 мм; степень монохроматичности (Dl/l), необходимую для того, чтобы такое число полос могло наблюдаться.
Ответ: N = 2500; Dl/l = 0,04 %.
2.2.10. Плосковыпуклая стеклянная линза с радиусом кривизны сферической поверхности 12,5 см сильно прижата к стеклянной пластинке. Диаметры десятого и пятнадцатого темных колец Ньютона в отраженном свете равны соответственно 1,0 и 1,5 мм. Определите длину волны света.
Ответ: 0,5 мкм.
2.2.11. Ширина 10 колец Ньютона, отсчитываемых вдали от их центра, равна 0,7 мм, ширина следующих 10 колец – 0,4 мм. Определите радиус кривизны линзы, если наблюдение производится в отраженном свете при длине волны 0,589 мкм.
Ответ: 0,22 м.
2.2.12. Две одинаковые плосковыпуклые линзы из кронгласа (n = 1,51) соприкасаются своими сферическими поверхностями. Определите оптическую силу такой системы, если в отраженном свете с длиной волны 0,60 мкм диаметр пятого светлого кольца Ньютона равен 1,5 мм. Каков диаметр пятого кольца, если пространство между линзами заполнено сероуглеродом (n С = 1,63)?
Ответ: 2,4 дптр; 1,13 мм.
2.2.13. На стеклянный клин падает нормально пучок света (l = 5,82×10–7 м). Угол клина q = 20². Какое число темных интерференционных полос приходится на единицу длины клина? Показатель преломления света n = 1,5.
Ответ: N = 5 см–1.
2.2.14. Мыльная пленка, расположенная вертикально, образует клин вследствие стекания жидкости. Наблюдая интерференционные полосы в отраженном свете ртутной дуги (l = 546,1 нм), находим, что расстояние между пятью полосами l = 2 см. Найти угол q клина. Свет падает перпендикулярно к поверхности пленки. Показатель преломления мыльной воды n = 1,33.
Ответ: q = 8,46².
2.2.15. Найти минимальную толщину d min пленки с показателем преломления n = 1,33, при которой свет с длиной волны l1 = 0,64 мкм испытывает максимальное отражение, а свет с длиной волны l2 = 0,40 мкм не отражается совсем. Угол падения света a = 30 °.
Ответ: d min = 0,65 мкм.
2.2.16. В опыте Ллойла (см. рисунок) световая волна, исходящая непосредственно из источника S (узкой щели), интерферирует с волной, отраженной от зеркала З. В результате на экране Э образуется система интерференционных полос. Расстояние от источника до экрана l = 100 см. При некотором положении источника ширина интерференционной полосы на экране D х = 0,25 мм, а после того как источник отодвинули от плоскости зеркала на D h = 0,60 мм, ширина полос уменьшилась в h = 1,5 раза. Найти длину волны света.
Ответ: l = 2D х ×D h / l (h – 1) = 0,6 мкм.
2.2.17. На рисунке показана интерференционная схема с бизеркалами Френеля. Угол между зеркалами a = 12¢, расстояние от линии пересечения зеркал до узкой щели S и экрана Э равно соответственно r = 10,0 см и b = 130 см. Длина волны света l = 0,55 мкм. Определить: а) ширину интерференционной полосы на экране и число возможных максимумов; б) сдвиг интерференционной картины на экране при смещении щели на d l = 1,0 мм по дуге радиуса r с центром в точке О; в) при какой максимальной ширине щели dmax интерференционные полосы на экране будут наблюдаться еще достаточно отчетливо?
Ответ: а) 
мм; N = 9; б) 
мм;
в) 
мкм.
2.2.18. Плоская световая волна падает на бизеркала Френеля, угол между которыми a = 2,0¢. Определить длину волны света, если ширина интерференционной полосы на экране D х = 0,55 мм.
Ответ: l = 2aD х = 0,64 мкм.
2.2.19. Плоская монохроматическая световая волна падает нормально на диафрагму с двумя узкими щелями, отстоящими друг от друга на расстояние d = 2,5 мм. На экране, расположенном за диафрагмой на l = 100 см, образуется система интерференционных полос. На какое расстояние и в какую сторону сместятся полосы, если одну из щелей перекрыть стеклянной пластинкой толщиной h = 10 мкм?
Ответ: В сторону перекрытой щели; D х = hl (n – 1) / d = 2 мм.
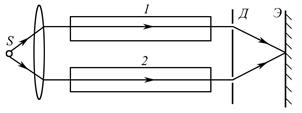
2.2.20. На рисунке показана схема интерферометра, служащего для измерения показателей преломления прозрачных веществ. Здесь S – узкая щель, освещенная монохроматическим светом l = 589 нм; 1 и 2 – две одинаковые трубки с воздухом, длина каждой из которых l = 10,0 см; Д – диафрагма с двумя щелями, интерференционная картина на экране Э сместилась вверх на N = = 17 полос. Показатель преломления воздуха n = 1,000277. Определить показатель преломления аммиака.
Ответ: n ¢ = n + N l/ l = 1,000377.
2.2.21. На тонкую пленку (n = 1,33) падает параллельный пучок белого света. Угол падения i 1 = 52°. При какой минимальной толщине пленки зеркально отраженный свет будет наиболее сильно окрашен в желтый цвет (l = 0,60 мкм)?
Ответ: d = 0,14 мкм.
2.2.22. Найти минимальную толщину пленки с показателем преломления 1,33, при которой свет с длиной волны 0,64 мкм испытывает максимальное отражение, а свет с длиной волны 0,40 мкм не отражается совсем. Угол падения света равен 30°.
Ответ: 0,60 мкм.
2.2.23. Свет с длиной волны l = 0,55 мкм падает нормально на поверхность стеклянного клина. В отраженном свете наблюдают систему интерференционных полос, расстояние между соседними максимумами которых D х = 0,21 мм. Найти: а) угол между гранями клина; б) степень монохроматического света (Dl/l), если исчезновение интерференционных полос наблюдается на расстоянии l » 1,5 см от вершины клина.
Ответ: а) a = l/2 n D x = 3¢; б) Dl/l = 0,014.
2.2.24. Плосковыпуклая стеклянная линза с радиусом кривизны R = 40 см соприкасается выпуклой поверхностью со стеклянной пластинкой. При этом в отраженном свете радиус некоторого темного кольца r = 2,5 мм. Наблюдая за данным кольцом, линзу осторожно отодвинули от пластинки на D h = 10 мкм. Каким стал радиус этого кольца?
Ответ: 
мм.
2.2.25. На вершине сферической поверхности плосковыпуклой стеклянной линзы имеется сошлифованный плоский участок радиусом r 0 = 3,0 мм, которым соприкасается со стеклянной пластинкой. Радиус кривизны выпуклой поверхности линзы R = 150 см. Найти радиус шестого светлого коль