Литература
1. Математика: алгебра и начала математического анализа, геометрия. Алгебра и начала математического анализа.10-11 классы: учеб. для общеобразоват. организаций: базовый и углубл. уровни / [Ш.А.Алимов, Ю.М.Колягин, М.В.Ткачева и др.].- 3-е изд.- М.: Просвещение, 2016.
2. Валуцє И.И., Дилигул Т.Д. Математика для техникумов. - М., 1989.
3. Практические занятия по математике. / Н.В. Богомолов. - М., 1990.
4. Математика для техникумов. Алгебра и начала анализа. / Под ред. Г.Н. Яковлева. Ч. 1 – М., 1987.
5. Математика. Справочные материалы. Книга для учащихся./ Под ред. В.А.Гусева, А.Г.Мордковича-М.,1990.
Домашнее задание:
1. Выучить опорный конспект и [1] ГлX § 54; [3] Гл8 § 45
2. Ответить на вопросы 1-10 теста по теме «Интеграл и его приложения»
Ответы на задания присылать на мой электронный адрес: volovik-7373@mail.ru
ПЛАН – КОНСПЕКТ ЗАНЯТИЯ
РАЗДЕЛ 6. Интеграл и его приложения
ТЕМА 6.1Первообразная и ее свойства. Неопределенный интеграл и его свойства. Формулы интегрирования.
I АКТУАЛИЗАЦИЯ ЗНАНИЙ
«Мозговой штурм» - ответ на вопрос: какие операции имеют обратные и однозначны ли они?
На каждое действие есть противодействие. Так и в математике СЛОЖЕНИЕ-ВЫЧИТАНИЕ, УМНОЖЕНИЕ-ДЕЛЕНИЕ, ВОЗВЕДЕНИЕ В СТЕПЕНЬ-ИЗВЛЕЧЕНИЕ КОРНЯ. Причем, сложение, вычитание, умножение, деление, возведение в степень – ОДНОЗНАЧНЫЕ ОПЕРАЦИИ (ответ единственный), а вот извлечение корня – МНОГОЗНАЧНАЯ ОПЕРАЦИЯ,
Мы недавно изучили еще одну операцию – ОПЕРАЦИЮ ДИФФЕРЕНЦИРОВАНИ ФУНКЦИЙ, другими словами, операцию нахождения производной.
Если мы можем найти производную функции, то возможно ли по известной производной найти саму функцию (ее прежний образ)?!
IIМотивация учебной деятельности студентов
Задача. Производная некоторой функции есть функция 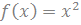 . Найдите эту функцию. Единственная ли такая функция?
. Найдите эту функцию. Единственная ли такая функция?
Решение.
Искомая функция - это 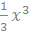 , действительно, (
, действительно, ( 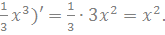
Но такая функция не единственна, функции 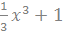 и
и 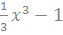 и
и 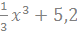 и
и 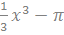 имеют производную равную
имеют производную равную 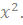
III ИЗУЧЕНИЕ НОВОГО МАТЕРИАЛА
Первообразная функция и неопределённый интеграл
Определение Первообразной для данной функции f(x) на данном промежутке 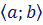 называется такая функция F(x), производная которой на этом промежутке равна f(x), т.е.
называется такая функция F(x), производная которой на этом промежутке равна f(x), т.е. 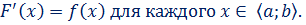
Например, функция F(x)=x3 является первообразной функции f(x)=3x2 на всей числовой оси, так как (x3)/=3x2 при любом x. Отметим, что вместе с функцией F(x)=x3 первообразной для f(x)=3x2 является любая функция вида Ф(х)=х3+С, где С – произвольное постоянное число.
Определение Совокупность всех первообразных, построенных для функции 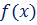 на интервале
на интервале 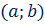 называется неопределенным интегралом от функции
называется неопределенным интегралом от функции 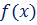 на интервале
на интервале 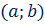 и обозначается
и обозначается 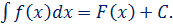
Свойства неопределённого интеграла
1. Производная от неопределенного интеграла равна подынтегральной функции
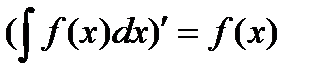
2. Дифференциал неопределенного интеграла равен подынтегральному выражению
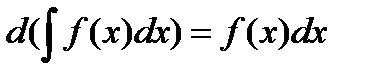
3. Неопределенный интеграл от дифференциала некоторой функции равен этой функции с точностью до постоянного слагаемого
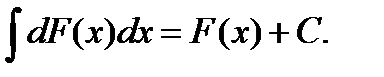 или
или 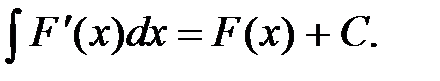
где С – произвольная постоянная
4. Постоянный множитель можно выносить за знак интеграла
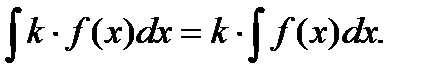
где k – некоторое число.
5. Интеграл от алгебраической суммы двух функций равен такой же сумме интегралов от этих функций
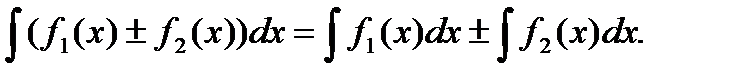
Таблица интегралов
1) 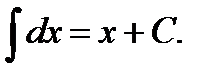
2) 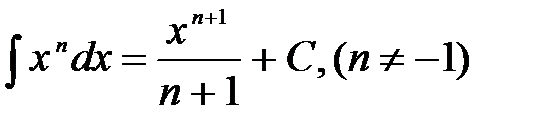 .
.
3) 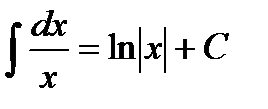 , в общем случае
, в общем случае 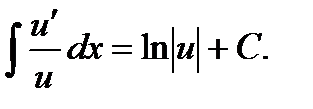
4) 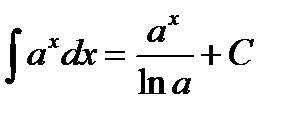 , в частности
, в частности 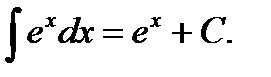
5) 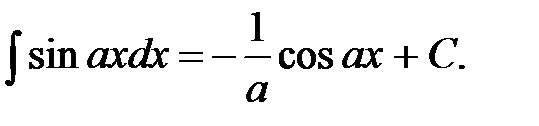 9)
9) 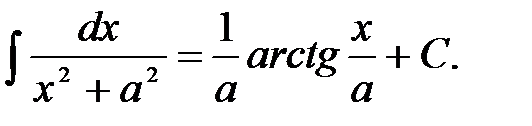
6) 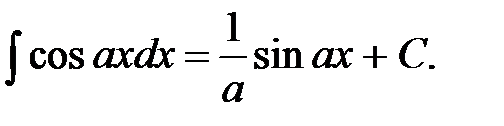 10)
10) 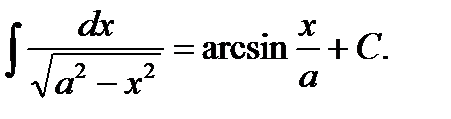
7) 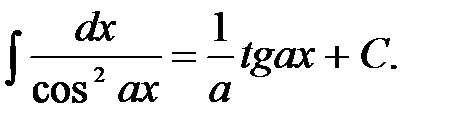 11)
11) 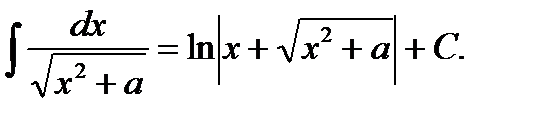
8) 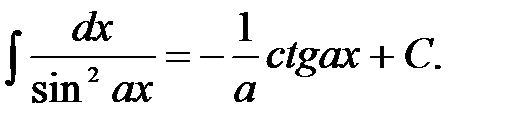 12)
12) 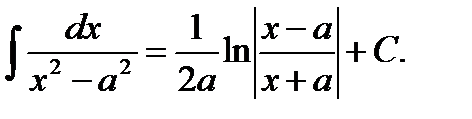
IVКОНТРОЛЬ -Домашнее задание:
1. Изучить опорный конспект и [1] ГлX § 54; [3] Гл8 § 45
2. Написать конспект темы и выучить его: определение первообразной и неопределенного интеграла и его свойства, формулы интегрирования (таблица интегралов)
3. Ответить на вопросы 1-10 теста по теме «Интеграл и его приложения»
ТЕСТОВЫЕ ЗАДАНИЯ ПО ТЕМЕ «Интеграл и его применение»
1. Первообразной функции f(x) на интервале (a;b) называют такую функцию F(x), что выполнено равенство:
А) F||(x)=f(x) 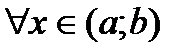 ; Б) F|(x)=f(x);
; Б) F|(x)=f(x);
В) dF(x)=f(x)dx; Г) F|(x)=f(x) 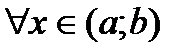 .
.
2. Первообразной функции f(x) = sin2x является функция:
А) F(x) = cos2x – 1; Б) F(x) = -1/2cos2x+π;
В) F(x) = -1/2cosx; Г) F(x) = 1/2sin2x+2.
3. Неопределенный интеграл от функции f(x)=х4-2 равен:
А) 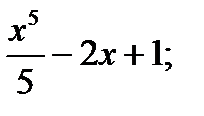 Б)
Б) 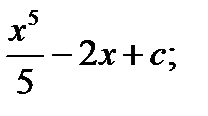 В)
В) 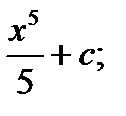 Г)
Г) 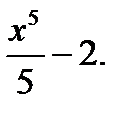
4. Графики любых двух первообразных функций можно получить один из другого:
А) параллельным переносом вдоль оси ОХ;
Б) параллельным переносом вдоль оси ОУ;
В) сжатием в 2 раза вдоль оси ОУ;
Г) другой ответ.
5. График первообразной для функции 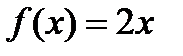 изображен на рисунке:
изображен на рисунке:
А) Б) В) Г)
у у уу
0 2 х 0 х 0 х х
6. Выбрать правильный ответ 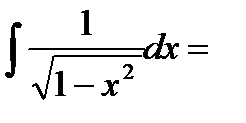
А) arcsinx+C; Б) arctgx+C;
В) 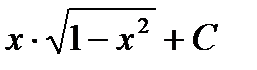 ; Г) другой ответ.
; Г) другой ответ.
7. Известно, что f/(x) = 2х, тогда функция f(x) равна:
А) 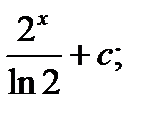 Б)
Б) 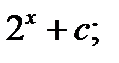 В)
В)  Г)
Г) 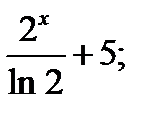
8. Известно, что 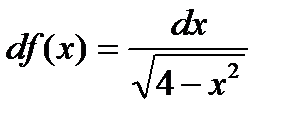 , тогда функция f(x) равна:
, тогда функция f(x) равна:
А) arcsin x/2 -2; Б) arcсos 2x +c; В) -arcsin 2x +2; Г) arcsin x/2 +c.
9. Известно, что 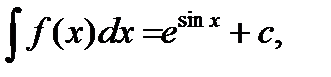 тогда функция f(x) равна:
тогда функция f(x) равна:
А) 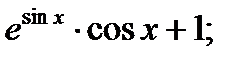 Б)
Б) 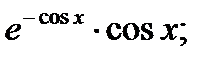 В)
В) 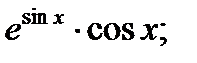 Г)
Г) 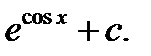
10. Функция 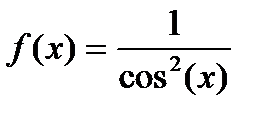 интегрируема на отрезке:
интегрируема на отрезке:
А) [−π∕2;π∕2]; Б) [0;π]; В) [−π∕4;π∕4]; Г) [π∕4;2π].
Преподавательvolovik-7373@mail.ru