Ранг матрицы.
Пусть 
Определение. Строчечным рангом матрицы называется размерность ее строчечного пространства 
. Столбцовым рангом матрицы называется размерность ее столбцового пространства 
.
Из определения строчечного (столбцового) ранга матрицы и понятия размерности подпространства следует, что строчечный (столбцовый) ранг матрицы – это число векторов-строк (векторов-столбцов), которые составляют базис строчечного (столбцового) пространства, т.е. это максимальное число ее линейно независимых строк (столбцов).
Пример. Найдем строчечный и столбцовый ранги матрицы 
.
Для вычисления строчечного ранга рассмотрим строки матрицы A. Первая строка ненулевая, поэтому система, составленная из этой строки, линейно независима. Если рассмотреть две первые строки, то несложно заметить, что вторая строка линейно выражается через первую, а поэтому две первые строки линейно зависимы. Аналогично, первая и третья строки линейно зависимы. Первая и четвертая строки линейно независимы. При добавлении к ним любой другой строки будем получать всегда линейно зависимые системы строк, а поэтому строчечный ранг матрицы равен двум.
Для вычисления столбцового ранга рассмотрим столбцы матрицы A. Несложно заметить, что оба столбца матрицы линейно независимы, а значит, столбцовый ранг матрицы равен двум. Получили, что в рассмотренном примере строчечный и столбцовый ранги матрицы совпадают. оказывается это имеет место в общем случае.
Теорема 1. Строчечный и столбцовый ранги матрицы совпадают.
Доказательство. Если матрица нулевая, то 
. Пусть , – ненулевая матрица и 
, а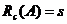 
.
Так как , то 
, т.е. базис строчечного пространства матрицы состоит из k векторов-строк. Составим из этих строк матрицу C. C – матрица размерности k на n, через строки которой линейно выражаются все строки матрицы A. Тогда по следствию из леммы о строчечном пространстве произведения матриц, существует матрица B размерности m на k такая, что 
. Теперь применяя лемму для столбцового пространства произведения матриц можем утверждать, что 
. Откуда следует, что 
, а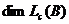 
, в свою очередь, не превосходит числа столбцов матрицы B, т.е. 
. С другой стороны, 
. Таким образом, получили, что 
.
Аналогичными рассуждениями, рассматривая столбцовый ранг матрицы A, можно показать, что 
(проведите рассуждения самостоятельно). Итак, 
■
Теорема 1 доказывает корректность следующего определения.
Определение. Рангом матрицы называется общее значении ее строчечного и столбцового ранга.
Таким образом, чтобы найти ранг матрицы по определению, нужно рассмотреть ее строки (или столбцы) и определить максимальное число линейно независимых.
Проще всего это сделать, если матрица имеет особый вид.
Определение. Матрицей ступенчатого вида называется матрица, у которой в каждой строке, начиная со второй, первый ненулевой элемент расположен правее первого ненулевого элемента предыдущей строки.
Например, 
– матрица ступенчатого вида. Несложно вычислить ее ранг. В рассмотренном примере он равен двум. В общем случае: ранг матрицы ступенчатого вида равен числу ее ненулевых строк (уметь проводить обоснования на примерах и в общем виде).
В общем случае пользоваться определением ранга матрицы неудобно – нужно перебирать разные системы векторов-строк. Другой способ вычисления ранга, которым мы и будем применять на практике, основан на так называемых элементарных преобразованиях матрицы.
Определение. Элементарными преобразованиями матрицы называют:
· перестановку двух ее строк (столбцов) местами:
;
· умножение строки (столбца) на число, отличное от нуля:
;
· прибавление к строке (столбцу) другой строки (другого столбца), умноженной на любое число:
.
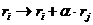
Теорема 2. Ранг матрицы не изменяется при элементарных преобразованиях.
Доказательство. Рассмотрим несколько случаев.
1) Пусть матрица B получена из матрицы A с помощью перестановки двух строк местами, т.е. 
, 
, 
, если 
. 
. А 
.
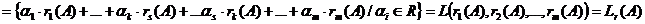Следовательно, 
, а значит, и 
, т.е. 
.
2) Пусть матрица B получена из матрицы A с помощью умножения некоторой ее строки на число, отличное от нуля, т.е. 
, , если 
. 
.
Следовательно, , а значит, и , т.е. .
3) Пусть матрица B получена из матрицы A с помощью прибавления к некоторой ее строке другой строки, умноженной на число, т.е. 
, , если .
.
Следовательно, , а значит, и , т.е. .
4) Если матрица B получена из матрицы A цепочкой преобразований ее строк, то по транзитивности, применяя 1)-3), получим, что ранги этих матриц будут равны ■
Теорема 2 дает алгоритм вычисления ранга матрицы:
С помощью элементарных преобразований привести матрицу к ступенчатому виду.
Вычислить ранг матрицы ступенчатого вида (равен числу ее ненулевых строк).
Определить ранг исходной матрицы (совпадет с рангом полученной матрицы ступенчатого вида).
Пример.