КАЛЕНДАРНЫЙ ПЛАН
«Теория функций комплексного переменного и гармонический анализ»
Для студентов-бакалавров факультетов «Э» и РКТ 2 курса, 4семестра
Уч. г.
ЛИТЕРАТУРА
Основная
1. Власова Е.А. Ряды. Под редакцией В.С.Зарубина, А.П. Крищенко.- М.: МГТУ.- 2006. 612с. (Серия Математика в техническом университете, вып. IX).
2. Пискунов Н.С. Дифференциальное и интегральное исчисление для втузов. Т.2,
3 зд. - М.: Наука, 1985.- 560с.
3.Бугров Я.С., Никольский С.М. Дифференциальные уравнения. Кратные интегралы. Ряды. Функции комплексного переменного. - М.: Наука. - 1989.- 464с.
4. Ильин В.А., Позняк Э.Г. Основы математического анализа. Ч.1,2.- М.: Наука. - 1982, 616с.
5. Кудрявцев Л.Д. Курс математического анализа. - Т.1, 2.- М.: Высшая школа. 1981.- 614 с., 470с.
6. Морозова В.Д. Теория функций комплексного переменного. Под редакцией Зарубина В.С., Крищенко А.П. М.: МГТУ, 2000.
7. Араманович И.Г., Лунц Г.Л., Эльсгольц Л.Э. Функции комплексного переменного. Операционное исчисление. М.: Наука, 1986.
8. Свешников А.Г., Тихонов А.Н. Теория функций комплексного переменного. М.: Наука, 1986.
9. Сборник задач по математике для втузов, т.2. Под редакцией Ефимова А.В., Демидовича Б.П. М.: Наука, 1986.
10. Задачи и упражнения по математическому анализу для втузов. Под ред. Демидовича Б.П.- М.: Интеграл-пресс, 1997.- 416с
Дополнительная
11. Краснов М.Л., Киселев Л.И., Макаренко Г.И. Функции комплексного переменного. Операционное исчисление. Теория устойчивости. Задачи и упражнения. М.: Наука, 1981.
12. Томашпольский В.Я., Шевченко М.Н., Янов И.О. Числовые ряды. Методические указания к выполнению типового расчета.- М.: МГТУ, 2006.
13. Дубограй И.В., Дьякова Л.Н., Скуднева О.В. Степенные ряды. Методические указания. -М.: Изд. МГТУ, 2005. 57 с.
|
|
14. Нараленков К.М., Шарохина И..В., Тригонометрические ряды Фурье. Методические указания. -М.: Изд. МГТУ, 2005. 40 с
15. Абрагин А.В., Дубровин В.М. Теория функций комплексного переменного. Методические указания к выполнению домашнего задания. М.: МГТУ, 2006.
16. Агаева Э.И., Ершова М.И., Зотина Р.С. Пособие по теории функций комплексного переменного. М.: МГТУ, 1992.
17. Алгазин О.Д., Бутина Т.А., Дубровин В.М. Операционное исчисление. М: МГТУ, 2012.
ЛЕКЦИИ.
Модуль 1: Гармонический анализ
Лекции 1-2. Числовые ряды. Сходящиеся и расходящиеся ряды. Необходимый признак сходимости. Простейшие свойства сходящихся рядов (почленное сложение рядов, умножение ряда на число, отбрасывание конечного числа членов ряда). Знакоположительные ряды. Признаки сравнения. Признаки Даламбера и Коши. Интегральный признак Коши. Ряды Дирихле.
Л-1, гл. 1; Л - 2, гл.16, §1-5; Л-4 ч.1, гл.13, § 1,2,4.
Лекция 3. Знакопеременные ряды. Абсолютная и условная сходимость. Структура рядов, сходящихся абсолютно и условно, их свойства. Знакочередующиеся ряды. Признак Лейбница. Оценка суммы и остатка ряда.
Л-1, гл. 1; Л - 2, гл.16, § 5-8; Л-4, ч.1, гл.13, § 3-5.
Лекция 4. Функциональные ряды. Область сходимости функционального ряда. Равномерная сходимость. Признак Вейерштрасса равномерной сходимости. Свойства равномерно сходящихся рядов; непрерывность суммы, почленное интегрирование и дифференцирование (без док-ва). Степенные ряды. Теорема Абеля.
Л-1, гл. 2; Л - 2, гл.16, §9-13; Л-4, ч.2, гл.1, §1,2,4.
Лекция 5. Интервал, радиус и область сходимости степенного ряда. Свойства степенных рядов: равномерная сходимость, непрерывность суммы, почленное интегрирование и дифференцирование.
|
|
Л-1, гл. 2; Л - 2, гл.16, §13-15; Л-4, ч.2, гл.1, § 4,5.
Лекции 6. Разложение функции в степенной ряд. Ряд Тейлора и Маклорена. Теорема о разложении функции в ряд Тейлора. Разложение в ряд Маклорена функций: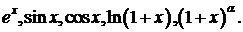 
Л-1, гл. 2; Л - 2, гл.16, §15-23.
Лекции 7-8. Ортогональность системы тригонометрических функций на отрезках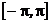 
и 
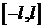. Тригонометрические ряды Фурье и коэффициенты Эйлера-Фурье. Теорема Дирихле (без док-ва). Разложение в ряд Фурье периодических, четных и нечетных функций. Неполные ряды Фурье. Разложение функций в ряд Фурье на произвольном отрезке длины 
. 
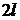Комплексная форма ряда Фурье.
Л-1, гл. 3.4; Л - 2, гл.17,§ 1-7, Л-4, ч.2, гл.10, §1 - 4.
Лекция 9. Разложение функций по произвольной полной ортогональной системе. Неравенство Бесселя и равенство Парсеваля. Полнота тригонометрической системы.
Л-1, гл. 3,6.