Глава 2
II и III законы термодинамики.
I закон утверждает что при превращении одной формы энергии в другую, общее количество энергии сохраняется.
Однако многие процессы характеризуются естественным направлением.
II закон устанавливает критерий, позволяющий предсказать, может ли данный процесс идти самопроизвольно или нет.
Величина, характеризующая возможность самопроизвольного осуществления химической реакции или физического изменения в изолированной системе называется S – энтропией и является функцией состояния вещества, dS – полный дифференциал.
III закон позволяет получать абсолютное значение S вещества.
1 Интенсивные и экстенсивные (макроскопические) свойства вещества.
Интенсивные свойства вещества – не зависят от количества вещества в системе, этими свойствами являются T, P, ρ.
Экстенсивные свойства пропорциональны массе системы, если интенсивные свойства поддерживаются неизменными. Экстенсивными свойствами являются V, U.
В статистической физике в этом случае говорят о свойстве аддитивности: например, энергия системы равна сумме энергий отдельных её микроскопических частей. U обладает свойством аддитивности.
Экстенсивными свойствами являются: S, F (изохорный потенциал), G (изобарный потенциал) – свободная энергия Гиббса (в стат.физике «термодинамический потенциал»)
Интенсивные свойства: μ; частные производные: 
, 
, 
, 
, 
, 
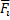по количеству вещества.
Самопроизвольные и несамопроизвольные процессы. II закон термодинамики.
Хорошо известно, что многие процессы идут самопроизвольно:
Самопроизвольный процесс, т.е. без внешних воздействий, когда система, предоставленная самой себе, может быть источником работы.
|
|
(самопроизвольные процессы не идут в обратном направлении)
Несамопроизвольный процесс – обратный по отношению к самопроизвольному процессу. Он возможен только лишь при использовании энергии другого самопроизвольного процесса.
II закон рассматривается как постулат о справедливости которого следует судить по результатам его применения. Он справедлив для макросистем, так как всегда выполняются соотношения выведенные из II закона.
Формулировка Кельвина:
Процесс является самопроизвольным, если протекание его в изолированной системе приводит к увеличению энтропии системы.
Невозможно использовать циклический процесс для превращения в работу теплоты, взятой из теплового источника, без одновременного переноса некоторого количества теплоты от более горячего тела к более холодному.
Формулировка Клазиуса:
Невозможно использовать циклический процесс для переноса теплоты от более холодного тела к более горячему без одновременного превращения некоторого количества работы в q.
Подход Гиббса вводит величины, которые можно непосредственно применить к химическим реакциям.
S даёт информацию о возможности самопроизвольного осуществления химической реакции или физического изменения.
Энтропия S – функция состояния системы, т.е. она имеет (как и U) конкретное численное значение, когда система находится в определенном состоянии.
Определение:
dS определяется: для бесконечно малого обратимого изменения
dS≡ 
/T,
(2.1)
где Т определяется этим соотношением.
Индекс «обр», т.е. «для обратимого процесса» позволяет утверждать, что - полный дифференциал.
|
|
Т является интегрирующим множителем для dq=полный дифференциал.
Изменение S, сопровождающее данное изменение состояния не зависит от пути перехода. ∆S получается интегрированием (2.1) по обратимому пути от состояния 1 до состояния 2:
∆S=S2-S1= 
(2.2)
Любой обратимый путь между состояниями 1 и 2 даст то же значение.
S – экстенсивное свойство, так как зависит от массы системы.
II закон: для любого бесконечно малого процесса дифференциал dS больше чем 
или равен этой величине.
; dS≥ 
(2.3)
Т.о. существует два типа изменений:
Изменения, для которых dS> являются необратимыми.
Изменения, для которых dS= - обратимые.
II закон даёт критерий возможности протекания химической реакции.
Если dS> применимо к данному изменению состояния или данной химической реакции, то это изменение или реакция произойдет самопроизвольно. (В необратимом процессе все изменения идут самопроизвольно)
Применим (2.3) к изолированным системам, т.е. это системы с U=const, V=const, которые не обмениваются с окружающей средой ни q, ни w, ни веществом.
Тогда для изолированной системы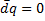 
, применив уравнения 2.1 и 2.3, получим:
Для бесконечно малого обратимого изменения:
dS=0
(2.4)
Для бесконечно малого необратимого изменения
dS>0
(2.5)
Для конечного обратимого изменения в изолированной системе ∆S=0.
Для конечного необратимого изменения в изолированной системе ∆S>0.
Таким образом, когда в системе происходит необратимое изменение, S возрастает.
Когда все возможности увеличения S при самопроизвольных изменениях будут исчерпаны, S имеет максимальное значение. Для любого бесконечно малого изменения состояния при равновесии в изолированной системе dS=0. Изменение S можно вычислить для трех простых обратимых процессов: фазовые переходы, нагревание вещества и расширение идеального газа.
|
|