Умножение вектора на число
Любой n-мерный вектор А можно умножить на любое число λ, при этом все его координаты умножаются на это число:
λA=(λ*a1, λ*a2,..., λ*an)
Пример: A=(1,2,3); λ=2; A*λ=(1*2,2*2,3*2)=(2,4,6)
Сложение векторов
Два вектора одинаковой размерности можно сложить, при этом их соответствующие координаты складываются:

Свойства линейных операций:
§ А + В = В + А
§ (А + В) + С = А+(В + С)
§ λ(А + В) = λА + λВ
§ (λ+ μ)А = λА + μ А
§ λ(μ А) = (λμ)А
Пример: 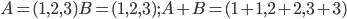
Определение скалярного произведения. Свойства скалярного произведения
Скалярное произведение векторов
Скалярным произведением векторов  и
и  называется величина, вычисляемая по формуле:
называется величина, вычисляемая по формуле:

Свойства произведения:
§ 
§ 
§ λ(A*B)=λ*A*B
Пример: 
Неравенство Коши-Буняковского. Неравенство треугольника (док-во)
Неравенство Коши-Буняклвского: |AB| =<|A||B|
Неравенство треугольника: |A+B|=<|A|+|B|
Доказательство: Так как AB=<|AB| и ||AB|=<|A||B|. Теперь используя полученные неравенства, имеем |A+B|^2=(A+B)^2=A^2+2AB+B^2=<|A|^2+2|A||B|+|B|^2=(|A|+|B|)^2, т.е. |A+B|^2=<(|A|+|B|)^2. Отсюда |A+B|=<|A|+|B|
Угол между n-мерными векторам. Теорема о равенстве векторов
Угол между векторами

Теорема: Ненулевые n-мерные вектора A и B равны, когда угол φ между ними равен 0 и |A| и |B| равны.
Док-во: A=B (*A)=> AA=AB(при этом A=B) => AA=BB => √(AA)=√(BB) => |A|=|B|
Cos(A,B)=AB/|A||B|(при этом A=B) = AA/|A||A| => A²/ |A|²=1 => φ=0
Коллинеарные вектора: A и B коллинеарны, если угол между ними равен 0 или π;
а) если AˆB=0, то коллинеарные векторы одинаково направленные;
б) если AˆB=π, то коллинеарные векторы противоположно-направленные.
Теорема: Ненулевые вектора A и B коллинеарны, когда можно подобрать такое число K, чтобы B=KA.
|
|
Система векторов называется разрешённой, если она в качестве части содержит диогональную систему векторов
Разложение вектора по системе векторов. Свойства разложения
Дана система n-мерных векторов A1,A2,…,Ak
Выберем k произвольных чисел: l1,l2,…,lk
l1A1+l2A2+…+lkAk (линейная комбинация векторов A1,A2,…,Ak с коэффициентами l1,l2,…,lk)
Пусть задан вектор B. Говорим,что вектор B линейно выражается через векторы A1,A2,…,Ak, если B=некоторой линейной комбинации векторов A1,A2,…,Ak, т.е. существует набор чисел l1,l2,…,lk такой, что B= l1A1+l2A2+…+lkAk
Коэффициенты l1,l2,…,lk называются в этом случае коэффициентами разложения вектора B по системе векторов A1,A2,…,Ak
Свойства:
1) нулевой вектор θ разлагается по любой системе векторов (θ=0*A1+0*A2+…+0*Ak )
2) если вектор B разлагается по части системы векторов, то он разлагается и по всей системе векторов (B=l2A2+l3A3+l4A4
B=0*A1+l2A2+l3A3+l4A4+0*A5)
3) каждый n-мерный вектор B разлагается по диагональной системе n- мерных векторов. B=(b1,b2,…,bn)
E1=(1,0,0,….0)
E2=(0,1,0,…,0)
………………
En=(0,0,0,…,1)
c коэффициентами = координатам вектора B
B=b1E1+b2E2+…+bnEn
Элементарные преобразования системы векторов
Система векторов {A1,…Am,B}. Запись в виде матрицы, столбцы которой совпадают с координатами векторов: A1 A2 … Am | B
a1 a2 … am | b1
……………. | …
an an … anm | bn
a) вычеркивание из матрицы нулевой строки
b) умножение j-ой координаты векторов на числа, отличное от 0
c) прибавление к j-ой строки i-ой строки, умноженной на любое число
d) после каждого элементарного преобразования вектор B преобразованной системы разлагается по системе A1,A2,…,Am с теми же коэффициентами, что и начальный.
|
|
Жорданово преобразование системы векторов.
Жордановым преобразованием системы векторов с разрешающим элементом Ars не равном 0 называется совокупность элементарных преобразований. Цель Жордановых преобразований получить единичный вектор.
Метод Гаусса: позволяет получить после конечного числа Жордановых преобразований разрешённую систему векторов. В каждом Жордановом преобразовании разрешающий элемент выбирается в строке, в которой ранее разрешающий элемент не выбирался.