Тема 4. Математические доказательства

Методические рекомендации

Задания под номером 10 в контрольной работе, предлагаемые по данной теме, связаны с оценкой правильности сделанного умозаключения, либо с его построением.

При анализе умозаключения выделяют его логическую структуру, а затем проверяют соответствие полученной схемы одному из известных правил вывода. Если такое соответствие имеет место, то рассуждение правильно, если же нет, то надо провести дальнейший анализ умозаключения. Для этого выделенную схему записывают на теоретико-множественном языке и с помощью кругов Эйлера изображают посылки, считая их истинными. Затем выясняют, всегда ли при этом истинно заключение. Если возможна ситуация, при которой заключение оказывается ложным, то умозаключение неправильно.

При решении задач другого типа требуется самостоятельно построить правильное умозаключение. В этих случаях надо ориентироваться на какую-либо из известных схем правильных умозаключений.

Образец выполнения заданий

Задание 10. Правильные и неправильные умозаключения

Задача. Правильно ли умозаключение: «Все студенты нашей группы закончили педучилище. Студентка b не закончила педучилище. Следовательно, она не учится в нашей группе».

Решение.

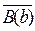1 способ. Выделим логическую структуру умозаключения, для этого обозначим через А(х) предложение «х – студентка нашей группы», через В(х) – предложение «х – закончила педучилище». Тогда первая посылка имеет вид: А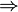(х) В(х).

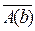Вторая посылка:.

Заключение:, где b – данная студентка.

Полученная схема

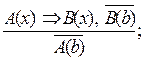является правилом отрицания. Следовательно, рассуждение правильно.

2 способ. Данное умозаключение запишем на теоретико-множественном языке.

Первая посылка. В ней утверждается, что множество (А) студентов группы является подмножеством множества (В) студентов, окончивших педучилище, т.е. что А Ì В.

Вторая посылка. Утверждается, что студентка b не заканчивала педучилище, т.е. что b ∉ В.

Заключение. Утверждается, что она не является студенткой группы, т.е. b ∉ А.

Схема умозаключения на теоретико-множественном языке имеет вид:

А Ì В, b ∉ В

b ∉ А

Изобразим посылки с помощью кругов Эйлера (рис. 5). Видим, что если А Ì В и b ∉ В, то при этом обязательно b ∉ А.

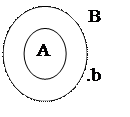Рис. 5

Данная схема такова, что истинность посылок гарантирует истинность заключения. Значит, рассуждение правильное.

Варианты контрольной работы

Вариант 1

1. Приведите примеры двух заданий из учебников математики для начальных классов, при выполнении которых осуществляется переход от одного способа задания множества к другому. Выбор обоснуйте.

2. Известно, что К – множество мальчиков класса, L – множество учащихся класса, занимающихся в кружке по рисованию. Сформулируйте условия, при которых: а) К∩L=Ø; б) К∩L=К.

3. Найти множество D = (A'∩ B) \ С, если А = (- ∞; 2), В = (0; 5], С = [3; 7)

4. Изобразите на координатной плоскости элементы множества X×Y, если:

X = {x | x N x ≤ 4},

Y = {y | y R y < 3}.

5. Из множества треугольников выделены подмножества прямоугольных, равнобедренных и тупоугольных треугольников. Произошло ли разбиение множества треугольников на классы?

6. Из 220 школьников 163 играют в баскетбол, 175 – в футбол, 24 не играют в эти игры. Сколько школьников одновременно играют в баскетбол и футбол?

7. Дайте определение прямоугольника, указав в качестве родового понятия понятие «четырехугольник», и выясните, являются ли прямоугольниками фигуры, изображенные на рисунке. Ответ обоснуйте.

8. Двуместный предикат P (x; y): «x + y = 11» определен на множестве А×А, где А = {4, 5, 6, 7}. Составьте таблицу значений этого предиката и укажите его множество истинности.

9. Вместо многоточия вставьте слова «необходимо», «достаточно» или «необходимо и достаточно», чтобы получилось истинное высказывание: «Для того чтобы разность двух чисел была четной, …, чтобы обе компоненты вычитания были четными».

10. Проверьте правильность рассуждения: «Во всяком прямоугольнике противоположные стороны равны. Четырехугольник ABCD – прямоугольник. Следовательно, его противоположные стороны равны».

Вариант 2

2. Известно, что А – множество спортсменов класса, В – множество отличников класса. Сформулируйте условия, при которых: а) В∩А≠Ø;

б) ВÌА.

3. Найти множество P = A È (B'_R \ C), если А = [0; 3), В = (-∞; 2) 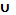[5; +∞),

С = [4; 7).

4. Изобразите на координатной плоскости элементы множества X×Y, если:

X = {x | x R -2 < x ≤ 3},

Y = {y | y Z 0 < x < 4}.

5. Произведите разбиение на классы множества целых чисел, используя свойства «быть кратным 4» и «быть кратным 5».

6. Из 38 учащихся класса 24 занимаются в хоре и 15 в лыжной секции. Сколько учащихся занимается и в хоре, и в лыжной секции, если в классе нет учащихся, не посещающих занятий хора или лыжной секции?

7. Дайте определение прямоугольника, указав в качестве родового понятия «параллелограмм», выясните, являются ли прямоугольниками фигуры, изображенные на рисунке. Ответ обоснуйте.

8. На множестве X = {-3, -2, -1, 1, 2, 3, 4, 5, 6, 7, 8} заданы предикаты A(x): «x – отрицательное число», В(x): «x – четное число». Найти множество истинности предиката A(x) ˅ B(x).

9. Вместо многоточия вставьте слова «необходимо», «достаточно» или «необходимо и достаточно», чтобы получилось истинное высказывание: «Для того чтобы натуральное число делилось на 5, …, чтобы его десятичная запись оканчивалась цифрой 0».

10. Проверьте правильность рассуждения: «Если четырехугольник является прямоугольником, то его диагонали равны. В четырехугольнике ABCD диагонали равны. Следовательно, ABCD – прямоугольник».

Вариант 3

2. Известно, что А – множество желтых цветов в вазе, В – множество роз в вазе. Сформулируйте условия, при которых: а) А∩В=Ø; б) АÈ В=А.

3. Найти множество X = A'_R 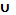B 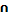C, если А = (-∞; 1), В = (0; 4),
С = [-3; 3).

4. Изобразите на координатной плоскости элементы множества X×Y, если:

X = {x | x Z -4 < x < 0},

Y = {y | y N y < 4}.

5. Укажите классы разбиения множества треугольников, которые получаются при рассмотрении таких свойств, как: «иметь хотя бы две равные стороны» и «иметь прямой угол».

6. Из 64 студентов на вопрос, занимаются ли они в свободное время спортом, утвердительно ответили 40 человек; любят ли они слушать музыку, 30 человек ответили утвердительно, причем 21 студент занимаются спортом и слушают музыку. Сколько человек не увлекается ни спортом, ни музыкой?

7. Дайте определение квадрата, указав в качестве родового понятия понятие «параллелограмм», и выясните, какие из фигур, изображенных на рисунке, являются квадратами, а какие – нет. Ответ обоснуйте.

8. На множестве X = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15} заданы предикаты A(x): «x – однозначное число», В(x): «x – четное число». Найти множество истинности предиката B(x) A(x).

9. Вместо многоточия вставьте слова «необходимо», «достаточно» или «необходимо и достаточно», чтобы получилось истинное высказывание: «Для того чтобы четырехугольник был ромбом, …, чтобы его диагонали были взаимно перпендикулярны».

10. Проверьте правильность рассуждения: «Все целые числа являются рациональными. Все рациональные числа – действительные. Следовательно, все целые числа – действительные».

Вариант 4

2. Пусть А – множество студентов группы, закончивших педагогическое училище, D – множество отличников группы. Сформулируйте условия, при которых: а) А∩D≠Ø; б) DÌА.

3. Найти множество P = (A \ B) 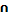(C 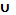B), если А = [-3; 0), В = [-1; 2),

С = (-2; 1].

4. Изобразите на координатной плоскости элементы множества X×Y, если:

X = {x | x N -2 < x < 3},

Y = {y | y R 1 < y ≤ 4}.

5. Из множества четырехугольников выделили следующие подмножества: а) прямоугольников, не являющихся ромбами; б) ромбов, не являющихся прямоугольниками; в) квадратов; г) четырехугольников, не являющихся ни ромбами, ни прямоугольниками. Произошло ли разбиение множества четырехугольников на классы?

6. Среди 35 туристов одним английским языком владеют 11 человек, английским и французским – 5 человек. 9 человек не владеют ни английским, ни французским. Сколько человек владеет только французским языком?

7. Дайте определение параллелограмма и выясните, какие из фигур, изображенных на рисунке, являются параллелограммами, а какие – нет. Ответ обоснуйте.

8. На множестве X = {-5, -4, -3, -2, -1, 0, 1, 2, 3, 4, 5} заданы предикаты A(x): «x – целое отрицательное число» и В(x): «x – четное число». Найдите множество истинности предиката А‾(x) Λ B(x).

10. Проверьте правильность рассуждения: «Если число делится на 3, то сумма цифр в записи этого числа делится на 3. Число 25 не делится на 3. Следовательно, сумма цифр в записи числа не делится на 3».

Вариант 5

2. Известно, что D – множество девочек класса, Е – множество учащихся класса, сидящих за первыми партами. Сформулируйте условия, при которых: а) D∩Е=Ø; б) D∩Е=Е.

3. Найти множество D = A 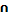B 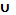C'_R, если А = [-3; 2), В = [0; 4],
С = (-∞; 2).

4. Изобразите на координатной плоскости элементы множества X×Y, если:

X = {x | x R -1 ≤ x < 4},

Y = {y | y R 1 ≤ y ≤ 3}.

5. Истинно ли высказывание: «Параллелограммы делятся на прямоугольники, ромбы и квадраты»? Почему?

6. Проведенное среди 50 школьников анкетирование показало, что в шахматы умеют играть 35 человек, в шашки – 40 человек, причем в обе игры умеют играть 21 человек. Сколько человек не умеет играть ни в шахматы, ни в шашки?

7. Дайте определение ромба, указав в качестве родового понятия понятие «параллелограмм», и выясните, какие из фигур, изображенных на рисунке, являются ромбами, а какие – нет. Ответ обоснуйте.

8. На множестве X = {1, 2, 3, …, 20} заданы предикаты A(x): «x – однозначное число» и В(x): «десятичная запись числа x не оканчивается цифрой 7». Найдите множество истинности предиката A(x) B(x).

9. Вместо многоточия вставьте слова «необходимо», «достаточно» или «необходимо и достаточно», чтобы получилось истинное высказывание: «Для того чтобы сумма двух чисел была больше 20, …, чтобы хотя бы одно слагаемое было больше 10».

10. Проверьте правильность рассуждения: «Если число нечетное, то оно не делится на 2. Число 17 – нечетное. Значит, число 17 не делится на 2».

Вариант 6

2. Проиллюстрируйте с помощью кругов Эйлера высказывания:

а) Некоторые четные натуральные числа кратны 7.

б) Все числа, делящиеся на 4, делятся на 2.

3. Найти множество X = (A 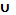B'_R) \ C, если А = [6; 9), В = (- ∞; 7) 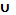[11; +∞), С = [8; 12].

4. Изобразите на координатной плоскости элементы множества X×Y, если:

X = {x | x R x < 3},

Y = {y | y R – 1 ≤ y ≤ 2}.

5. На множестве геометрических фигур плоскости выделены подмножества фигур, имеющих: а) центр симметрии; б) ось симметрии и в) не имеющих ни центра, ни оси симметрии. Можно ли считать, что произошло разбиение множества геометрических фигур на классы?

6. В группе туристов, состоящей из 100 человек, 10 человек не знали ни немецкий, ни французский языки, 75 знали немецкий, 83 знали французский. Сколько туристов знали два языка?

7. Дайте определение равностороннего треугольника. Используя данное определение, выясните, правильны ли следующие обоснования:

а) ABC – равносторонний, так как АВ = ВС;

б) DEF не является равносторонним, так как DE EF.

8. На множестве X = {-3, -2, -1, 0, 1, 2, 3, 4, 5} заданы предикаты С(x): «x – положительное число» и D(x): «x(x + 2) = 0». Найдите множество истинности предиката С(x) \/ D(x).

9. Дана теорема: «В любом ромбе диагонали взаимно перпендикулярны».

А. Переформулируйте данную теорему, используя слова «следует», «достаточно».

Б. сформулируйте теорему, равносильную данной, в соответствии с законом контрапозиции.

10. Проверьте правильность рассуждения: «Все прямоугольники являются параллелограммами. Во всех параллелограммах противоположные стороны равны. Следовательно, в любом прямоугольнике противоположные стороны равны».

Вариант 7

2. Проиллюстрируйте с помощью кругов Эйлера высказывания:

а) Ни один параллелограмм не является трапецией.

б) Любой квадрат является ромбом.

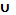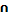3. Найти множество D = (A'_R B) C, если А = [-1; 4), В = (3; 6],
С = [-5; 0].

4. Изобразите на координатной плоскости элементы множества X×Y, если:

X = {x | x Z -4 < x ≤ -1},

Y = {y | y R y ≥ -2}.

5. Произведите разбиение множества целых чисел на классы, используя свойства «быть однозначным числом» и «быть двузначным числом».

6. В делегации 6 человек, знающих французский или немецкий язык. Трое из них говорят только на французском языке, двое – только на немецком. Сколько человек говорят на двух языках – французском и немецком?

7. Сформулируйте определение равнобедренного треугольника и на его основе выясните, правильны ли следующие обоснования:

а) ABC не является равнобедренным, так как АВ ВС;

б) DEF является равнобедренным, так как EF = FD.

Ответы обоснуйте.

8. На множестве X = {1, 2, 3, 4, …, 15} заданы предикаты P(x): «число x – простое» и Q(x): «число x оканчивается цифрой 5». Найти множество истинности предиката Pˉ(x) \/ Q(x).

9. Дана теорема: «Если каждое слагаемое делится на данное число, то и сумма делится на данное число».

А. Переформулируйте данную теорему, используя слова «следует», «достаточно», «необходимо».

Б. сформулируйте теорему, равносильную данной, в соответствии с законом контрапозиции.

10. Закончите умозаключение, используя правило заключения: «В любом прямоугольнике сумма внутренних углов равна 360 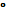. В четырехугольнике ABCD …». Ответ обоснуйте.

Вариант 8

2. Проиллюстрируйте с помощью кругов Эйлера высказывания:

а) Каждое из чисел, запись которого оканчивается цифрой 0, делится на 5.

б) Ни одно число, запись которого оканчивается цифрой 3, не делится на 6.

3. Найти множество P = (A 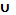B) \ (C 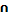B), если А = [-1; 2], В = [-5; 0),

С = [-3; 1).

4. Изобразите на координатной плоскости элементы множества X×Y, если:

X = {x | x R x > -3},

Y = {y | y N -2< y ≤ 3}.

5. Укажите, какие классы разбиения получаются при рассмотрении на множестве треугольников таких свойств: «иметь тупой угол» и «все углы острые».

6. Даны 40 чисел. Из них 10 чисел кратны 3, 15 чисел кратны 2, 20 чисел не кратны ни 2, ни 3. Сколько среди данных 40 чисел, кратных 6?

7. Соразмерны ли следующие определения:

а) биссектриса угла – это луч, делящий угол пополам;

б) равнобедренный треугольник – это треугольник, у которого хотя бы две стороны равны.

Ответы обоснуйте.

8. Двуместный предикат P (x, y): «x y» определен на множестве А × В, где А = {4, 8, 9, 10, 12, 13}, В = {2, 3, 4}. Составьте таблицу значений этого предиката и определите его множество истинности.

9. Сформулируйте признак делимости на 5, используя слова «тогда и только тогда, когда», «необходимо и достаточно». Выясните, какая из теорем выражает необходимый, а какая – достаточный признак делимости на 5:

А. Если число делится на 5, то его десятичная запись оканчивается цифрой 0 или 5.

Б. Если десятичная запись числа оканчивается цифрой 0 или 5, то число делится на 5.

10. Закончите умозаключение, используя правило заключения: «Если сумма цифр в записи числа делится на 9, то и само число делится на 9. В записи числа 3591 …». Ответ обоснуйте.

Вариант 9

2. Проиллюстрируйте с помощью кругов Эйлера высказывания:

а) Все квадраты являются четырехугольниками.

б) Некоторые равнобедренные треугольники являются прямоугольными.

3. Найти множество X = A'_R \ (B 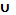C), если А = (-∞; 1), В = [1; 4),
С = (2; 5).

4. Изобразите на координатной плоскости элементы множества X×Y, если:

X = {x | x R 2 < x ≤ 6},

Y = {y | y R 1 ≤ y < 7}.

5. Произведено ли разбиение множества натуральных чисел на классы, если из него выделены подмножества чисел, делящихся на 3, и чисел, которые при делении на 3 дают остаток 1?

6. В школе 67 второклассников. Из них 36 занимаются гимнастикой, 52 – плаванием, а 4 учащихся освобождены от занятий физкультурой. Сколько учащихся занимаются и гимнастикой, и плаванием?

7. Соразмерны ли следующие определения:

а) ромбом называется четырехугольник, у которого все стороны равны;

б) прямоугольником называется ромб с прямым углом?

Ответы обоснуйте.

8. На множестве X = {-2, -1, 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10} заданы предикаты С(x): «число x кратно 3» и D(x): «x² + x – 2 = 0». Найти множество истинности предиката C‾(x) D(x).

9. Сформулируйте признак делимости на 3, используя слова «тогда и только тогда, когда», «необходимо и достаточно». Сформулируйте теоремы, выражающие необходимый, достаточный признак делимости на 3.

10. Закончите умозаключение, используя правило отрицания: «Во всяком прямоугольнике сумма внутренних углов равна 360 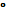. В четырехугольнике ABCD …». Ответ обоснуйте.

Вариант 10

2. Проиллюстрируйте с помощью кругов Эйлера высказывания:

а) Все мальчики 5 «А» класса участвовали в туристическом походе.

б) Ни один мальчик 5 «А» класса не является неуспевающим учеником.

3. Найти множество D = (A 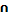B'_R) \ C, если А = [-4; 6), В = [3; 7), С = [2; 5].

4. Изобразите на координатной плоскости элементы множества X×Y, если:

X = {x | x R 1 ≤ x < 6},

Y = {y | y N -5 < y < 3}.

5. Множество треугольников разбито на три класса: равносторонних, прямоугольных и треугольников, не являющихся ни равносторонними, ни прямоугольными. Какие два свойства лежат в основе этой классификации?

6. В школе 67 второклассников. Из них 36 занимаются гимнастикой, 52 – плаванием, а 4 учащихся освобождены от занятий физкультурой. Сколько учащихся не занимаются гимнастикой?

7. Укажите, какие из сформулированных ниже определений избыточны, укажите, какие свойства являются следствиями остальных.

а) треугольником называется многоугольник, имеющий три стороны и три угла;

б) параллелограммом называется четырехугольник, у которого противоположные стороны попарно параллельны и равны.

8. Двуместный предикат P (x, y): «x + y ≤ 7» определен на множестве
А × А, где А = {2, 3, 4, 5}. Составить таблицу значений и указать область истинности этого предиката.

9. Дана теорема: «Если наклонные, проведены из одной точки к одной и той же прямой, равны, то равны и их проекции».

А. Переформулируйте данную теорему, используя слова «следует», «достаточно», «необходимо».

Б. Сформулируйте теорему, равносильную данной, в соответствии с законом контрапозиции.

10. Закончите умозаключение, используя правило отрицания: «Если сумма цифр в записи числа делится на 9, то и само число делится на 9. Число…».

Ответ обоснуйте.

Тема 4. Математические доказательства

Поиск по сайту