С щагом 0,1 и 0,01 изобразить на плоскости графики функций:
1.  2.
2. 
3. 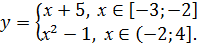 4.
4. 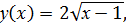
 .
.

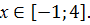

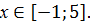
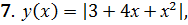
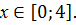 8.
8. 
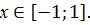
 ,
, 
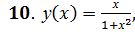
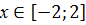 .
.
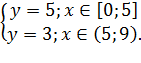
|
 ,
, 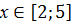 . 12.
. 12.  ,
, 
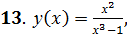
 . 14.
. 14.
15.  16.
16. 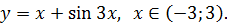
§ 3. Основные свойства и графики элементарных функций
1. ЛИНЕЙНАЯ ФУНКЦИЯ 
Свойства функции 
1) 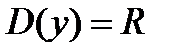 ;
;
2) 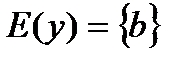 ;
;
3) Функция является четной;
4) Функция не является периодической;
5) При 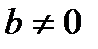 функция не имеет корней;
функция не имеет корней;
при  корнем функции является любое действительное число;
корнем функции является любое действительное число;
6) При 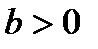 функция положительна на промежутке
функция положительна на промежутке 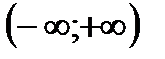 ,
,
при 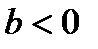 функция отрицательна на промежутке
функция отрицательна на промежутке 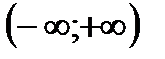 ;
;
7) График функции пересекает ось Оу в точке  ;
;
8) Промежутков возрастания и убывания нет. На всей области определения функция принимает одно и то же значение;
9) Точек максимума и минимума нет.
10) График функции – прямая (рис. 1–3).
у у
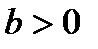
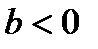
b
О х
О х
b
Рис.1 Рис.2
у

О х Рис. 3
Свойства функции 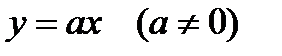
1) 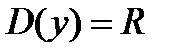 ;
;
2)  ;
;
3) Функция является нечетной;
4) Функция не является периодической;
5) Функция имеет единственный корень 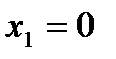 при любом
при любом 
График функции пересекает ось Ох в точке 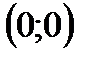 ;
;
6) При 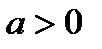 функция положительна на промежутке
функция положительна на промежутке 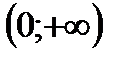 и отрицательна на промежутке
и отрицательна на промежутке  ; при
; при  функция положительна на промежутке
функция положительна на промежутке  и отрицательна на промежутке
и отрицательна на промежутке 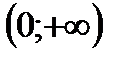 ;
;
7) График функции пересекает ось Оу в точке 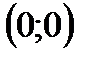 ;
;
8) При 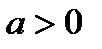 функция возрастает на всей области определения;
функция возрастает на всей области определения;
при  функция убывает на всей области определения;
функция убывает на всей области определения;
9) Точек максимума и минимума нет.
10) График функции – прямая (рис. 4–5).
у у


О х
О х
Рис.4 Рис.5
Свойства функции 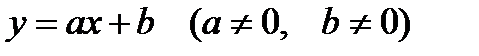
1) 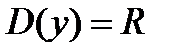 ;
;
2) 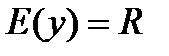 ;
;
3) Функция является функцией общего вида;
4) Функция не является периодической;
5) Функция имеет единственный корень 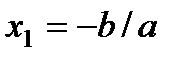 .
.
График функции пересекает ось Ох в точке 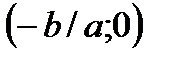 ;
;
6) При 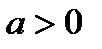 функция положительна на промежутке
функция положительна на промежутке  ,
,
отрицательна на промежутке 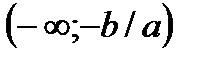 ; при
; при  функция положительна на промежутке
функция положительна на промежутке 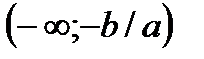 , отрицательна на промежутке
, отрицательна на промежутке 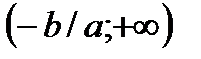 ;
;
7) График функции пересекает ось Оу в точке 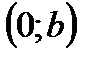 ;
;
8) При 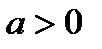 функция возрастает на всей области определения;
функция возрастает на всей области определения;
при  функция убывает на всей области определения;
функция убывает на всей области определения;
9) Точек максимума и минимума нет.
10) График функции – прямая (рис. 6-9).
 ,
, 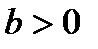
 ,
, 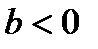
у у
b
О х
О х b
Рис.6 Рис.7
 ,
, 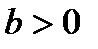
 ,
, 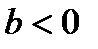
у у
b
О х
О х
Рис.8 Рис.9
2. СТЕПЕННАЯ ФУНКЦИЯ 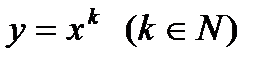
Свойства функции 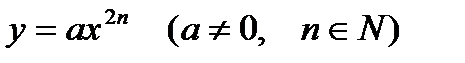
1) 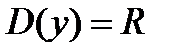 ;
;
2) 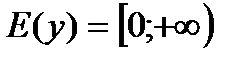 , если
, если  ,
, 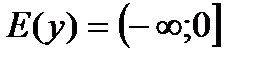 , если
, если  ;
;
3) Функция является четной;
4) Функция не является периодической;
5) Функция имеет единственный корень 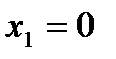 при любом
при любом 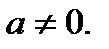 График функции касается оси Ох в точке
График функции касается оси Ох в точке 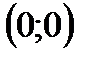 ;
;
6) При 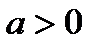 функция положительна на промежутках
функция положительна на промежутках  и
и  , при
, при 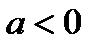 функция отрицательна на промежутках
функция отрицательна на промежутках  и
и  ;
;
7) График функции пересекает ось Оу в точке 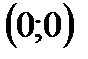 ;
;
8) При 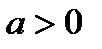 функция убывает на
функция убывает на  и возрастает на
и возрастает на  ; при
; при  функция возрастает на
функция возрастает на  и убывает на
и убывает на  ;
;
9) При 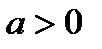 функция имеет минимум в точке
функция имеет минимум в точке 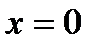 , причем
, причем 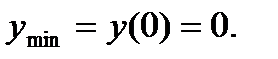 При
При  функция имеет максимум в точке
функция имеет максимум в точке 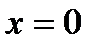 , причем
, причем  ;
;
10) График функции изображен на рис. 10-11.
у у


О х
О х
Рис.10 Рис.11
Свойства функции 
1) 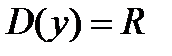 ;
;
2) 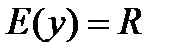 ;
;
3) Функция является нечетной;
4) Функция не является периодической;
5) Функция имеет единственный корень 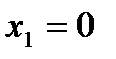 при любом
при любом 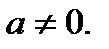 График функции пересекает ось Ох в точке
График функции пересекает ось Ох в точке 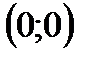 ;
;
6) При 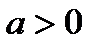 функция отрицательна на промежутке
функция отрицательна на промежутке  и положительна на промежутке
и положительна на промежутке  , при
, при 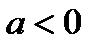 функция положительна на промежутке
функция положительна на промежутке  и отрицательна на промежутке
и отрицательна на промежутке  ;
;
7) График функции пересекает ось Оу в точке 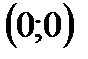 ;
;
8) При 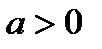 функция возрастает на всей области определения, при
функция возрастает на всей области определения, при  функция убывает на всей области определения;
функция убывает на всей области определения;
9) Функция не имеет минимумов и максимумов;
10) График функции изображен на рис. 12-13.
у у


О х
О х
Рис. 12 Рис. 13
Свойства функции 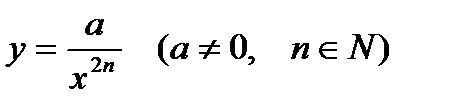
1) 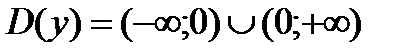 ;
;
2)  , если
, если  ,
, 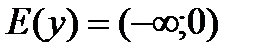 , если
, если  ;
;
3) Функция является четной;
4) Функция не является периодической;
5) Функция не имеет корней при любом 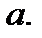 График не пересекает ось Ох;
График не пересекает ось Ох;
6) При 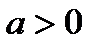 функция положительна на промежутках
функция положительна на промежутках  и
и  , при
, при 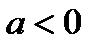 функция отрицательна на промежутках
функция отрицательна на промежутках  и
и  ;
;
7) График функции не пересекает ось Оу;
8) При 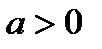 функция возрастает на
функция возрастает на  и убывает на
и убывает на  ; при
; при  функция убывает на
функция убывает на  и возрастает на
и возрастает на  ;
;
9) Функция не имеет минимумов и максимумов;
10) График имеет вертикальную асимптоту х= 0 и горизонтальную асимптоту 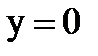 при
при 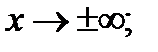
11) График функции изображен на рис. 14–15.
у у


О х
О х
Рис. 14 Рис. 15
Свойства функции 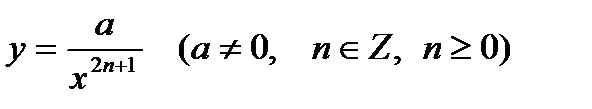
1) 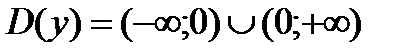 ;
;
2) 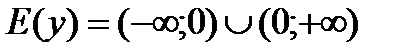 ;
;
3) Функция является нечетной;
4) Функция не является периодической;
5) Функция не имеет корней при любом 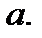 График функции не пересекает ось Ох;
График функции не пересекает ось Ох;
6) При 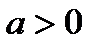 функция отрицательна на промежутке
функция отрицательна на промежутке  и положительна на
и положительна на  , при
, при 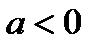 функция положительна на промежутке
функция положительна на промежутке  и отрицательна на
и отрицательна на  ;
;
7) График функции не пересекает ось Оу;
8) При 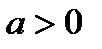 функция убывает на промежутках
функция убывает на промежутках  и
и  ; при
; при  функция возрастает на промежутках
функция возрастает на промежутках  и
и  ;
;
9) Функция не имеет минимумов и максимумов;
10) График имеет вертикальную асимптоту х= 0 и горизонтальную асимптоту 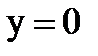 при
при 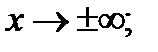
11) График функции изображен на рис. 16–17.
у у


О х
О х
Рис. 16 Рис. 17
3. КВАДРАТИЧНАЯ ФУНКЦИЯ 
Свойства функции 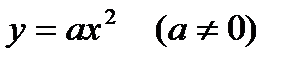
1) 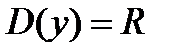 ;
;
2) 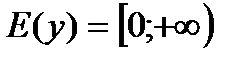 , если
, если  ,
, 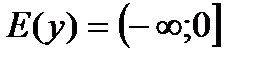 , если
, если  ;
;
3) Функция является четной;
4) Функция не является периодической;
5) Функция имеет единственный корень 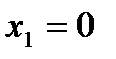 при любом
при любом 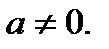
График функции касается оси Ох в точке 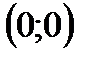 ;
;
6) При 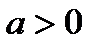 функция положительна на промежутках
функция положительна на промежутках  и
и  , при
, при 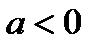 функция отрицательна на промежутках
функция отрицательна на промежутках  и
и  ;
;
7) График функции пересекает ось Оу в точке 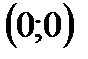 ;
;
8) При 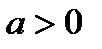 функция убывает на промежутке
функция убывает на промежутке  и возрастает на промежутке
и возрастает на промежутке  ; при
; при  функция возрастает на промежутке
функция возрастает на промежутке  и убывает на промежутке
и убывает на промежутке  ;
;
9) При 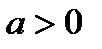 функция имеет минимум в точке
функция имеет минимум в точке 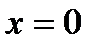 , причем
, причем 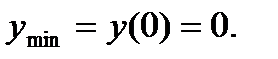
При  функция имеет максимум в точке
функция имеет максимум в точке 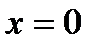 , причем
, причем 
10) График функции – парабола (рис. 18–19).
у у


О х
О х
Рис.18 Рис.19
Свойства функции 
1) 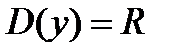 ;
;
2) 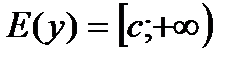 , если
, если  ,
, 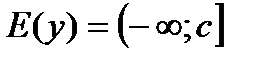 , если
, если  ;
;
3) Функция является четной;
4) Функция не является периодической;
5) Если  и
и 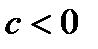 или
или  и
и 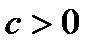 , то функция имеет два различных действительных корня:
, то функция имеет два различных действительных корня:  и
и 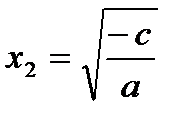 . В этих случаях график функции пересекает ось Ох в точках
. В этих случаях график функции пересекает ось Ох в точках  и
и 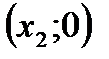 .
.
Если  и
и 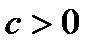 или
или  и
и 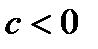 , то функция не имеет действительных корней. График не пересекает ось Ох и не касается ее, а расположен всюду выше Ох или всюду ниже Ох в соответствии со знаком а;
, то функция не имеет действительных корней. График не пересекает ось Ох и не касается ее, а расположен всюду выше Ох или всюду ниже Ох в соответствии со знаком а;
6) При  и
и 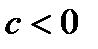 функция положительна на
функция положительна на  и
и 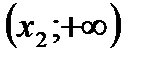 , а отрицательна на
, а отрицательна на 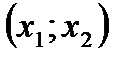 . При
. При  и
и 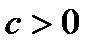 функция положительна на
функция положительна на  . При
. При  и
и 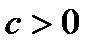 функция отрицательна на
функция отрицательна на  и
и 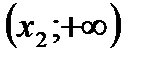 ; положительна на
; положительна на 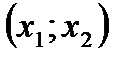 . При
. При  и
и 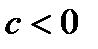 функция отрицательна на
функция отрицательна на  ;
;
7) График функции пересекает ось Оу в точке  ;
;
8) При 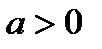 функция убывает на промежутке
функция убывает на промежутке  и возрастает на промежутке
и возрастает на промежутке  .
.
При  функция возрастает на промежутке
функция возрастает на промежутке  и убывает на промежутке
и убывает на промежутке  ;
;
9) При 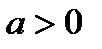 функция имеет минимум в точке
функция имеет минимум в точке 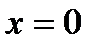 , причем
, причем 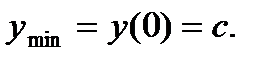 При
При  функция имеет максимум в точке
функция имеет максимум в точке 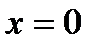 , причем
, причем 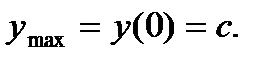
10) График функции – парабола (рис. 20–23).
 ,
, 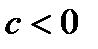
 ,
, 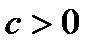
у у
с
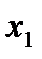 О
О 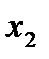 х
х
с О х
Рис. 20 Рис. 21
 ,
, 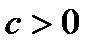
 ,
, 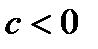
у у
с
О х
с
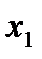 О
О 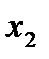 х
х
Рис. 22 Рис. 23
Свойства функции 
1) 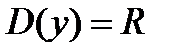 ;
;
2)  , если
, если  ,
,  , если
, если  ;
;
3) Функция является функцией общего вида;
4) Функция не является периодической;
5)  , где
, где 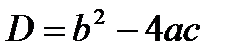 ;
;
6) При 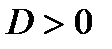 функция имеет два различных действительных корня:
функция имеет два различных действительных корня: 
 . График пересекает ось Ох в точках
. График пересекает ось Ох в точках  и
и 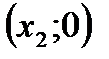 .
.
При 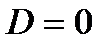 функция имеет один действительный корень:
функция имеет один действительный корень:  В этом случае график касается оси Ох в точке
В этом случае график касается оси Ох в точке  .
.
При  функция не имеет действительных корней. График не пересекает ось Ох и не касается ее, а расположен всюду выше оси Ох или всюду ниже оси Ох в соответствии со знаком числа а;
функция не имеет действительных корней. График не пересекает ось Ох и не касается ее, а расположен всюду выше оси Ох или всюду ниже оси Ох в соответствии со знаком числа а;
7) При 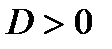 :
:  . При
. При 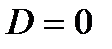 :
: 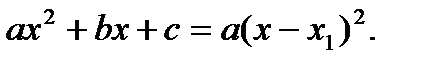 При
При  функция не разлагается на множители;
функция не разлагается на множители;
8) При  и
и 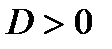 функция положительна на
функция положительна на  и
и 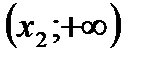 ; отрицательна на
; отрицательна на 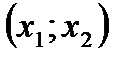 . При
. При  и
и 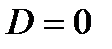 функция положительна на
функция положительна на  и
и  , а в точке
, а в точке  обращается в нуль. При
обращается в нуль. При  и
и  функция положительна на
функция положительна на  . При
. При  и
и 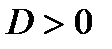 функция отрицательна на
функция отрицательна на  и
и 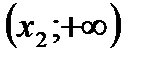 ; положительна на
; положительна на 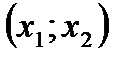 . При
. При  и
и 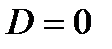 функция отрицательна на
функция отрицательна на  и
и  , а в точке
, а в точке  обращается в нуль. При
обращается в нуль. При  и
и  функция отрицательна на промежутке
функция отрицательна на промежутке  ;
;
9) График функции пересекает ось Оу в точке  ;
;
10) При 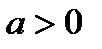 функция убывает на
функция убывает на 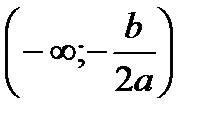 и возрастает на
и возрастает на  . При
. При  функция возрастает на
функция возрастает на 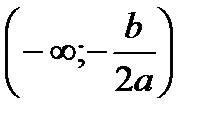 и убывает на
и убывает на  ;
;
11) При 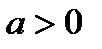 имеем:
имеем: 
При  имеем:
имеем: 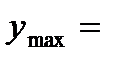
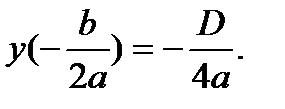
12) График функции – парабола (рис. 24–29).
 ,
, 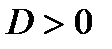
 ,
, 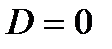
у у
с
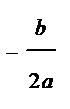
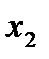 х
х 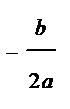 х
х
с
Рис.24 Рис. 25
 ,
, 
 ,
, 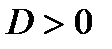
у у
с с
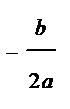 х
х 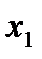
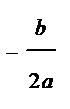
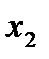 х
х
Рис. 26 Рис. 27
 ,
, 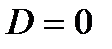
 ,
, 
у у
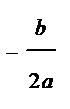 х
х
с 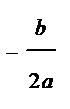 х с
х с
Рис. 28 Рис. 29
4. ПОКАЗАТЕЛЬНАЯ ФУНКЦИЯ  (
( ,
,  )
)
1. Область определения: 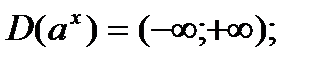
2. Область изменения: 
3. Функция не является ни четной, ни нечетной;
4. Функция не является периодической;
5. Функция не имеет корней. Ее график не пересекает ось Ох;
6. График функции пересекает ось Оу в точке с ординатой 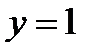 при любом
при любом 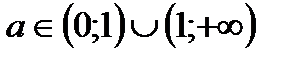 ;
;
7. Функция положительна на всей области определения;
8. Функция непрерывна на всей области определения;
9. Если  то функция
то функция 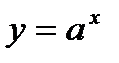 возрастает при
возрастает при 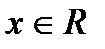 . Если
. Если 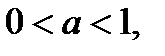 то функция
то функция 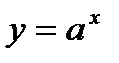 убывает при
убывает при  ;
;
10. Функция не имеет ни максимумов, ни минимумов.
11. Графики изображены на рис. 30-31.
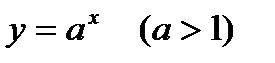 у
у

О 1 х Рис. 30
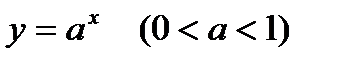 у
у
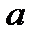
О 1 х Рис. 31
5. ЛОГАРИФМИЧЕСКАЯ ФУНКЦИЯ  (
( ,
,  )
)
1. 
2. 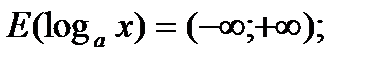
3. Функция не является ни четной, ни нечетной;
4. Функция не является периодической;
5. Функция имеет корень 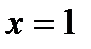 при любом а. Ее график пересекает ось Ох в точке
при любом а. Ее график пересекает ось Ох в точке 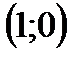 при любом
при любом 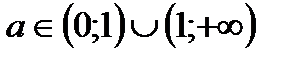 ;
;
6. График функции не пересекает ось Оу;
7. Если  то
то 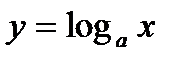 отрицательна при
отрицательна при 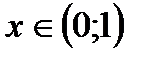 и положительна при
и положительна при 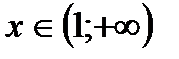 . Если
. Если 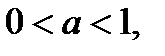 то функция
то функция 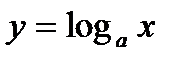 положительна при
положительна при 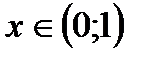 и отрицательна при
и отрицательна при 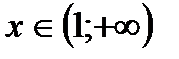 ;
;
8. Функция непрерывна на всей области определения;
9. Если  то
то 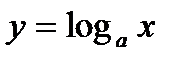 возрастает при
возрастает при 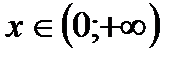 . Если
. Если 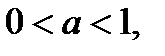 то функция
то функция 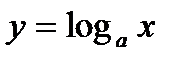 убывает при
убывает при 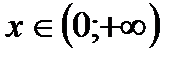 ;
;
10. Функция не имеет ни максимумов, ни минимумов.
11. Графики изображены на рис. 32-33.
 у
у
1
Рис. 32 О 1  х
х
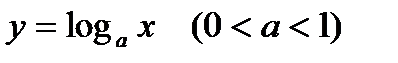 у
у
О 1 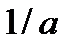 х
х
-1
Рис. 33
6. ФУНКЦИЯ МОДУЛЯ ЧИСЛА 
Свойства функции 
1) 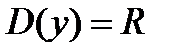 ;
;
2) 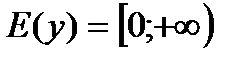 ;
;
3) Функция является четной;
4) Функция не является периодической;
5) Функция имеет один корень 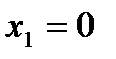 . График функции касается оси Ох в точке
. График функции касается оси Ох в точке 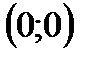 ;
;
6) Функция положительна на промежутках  и
и  ; в точке
; в точке  обращается в нуль;
обращается в нуль;
7) График функции пересекает ось Оу в точке 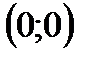 ;
;
8) Функция убывает на промежутке  , возрастает на
, возрастает на  ;
;
9) Функция имеет минимум в точке  , причем
, причем  ;
;
10) График функции указан на рис. 34.
у
у=–х у=х
О х Рис. 34
Функция 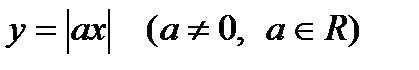 обладает теми же свойствами, что и функция
обладает теми же свойствами, что и функция 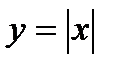 . Ее график изображен на рис. 35.
. Ее график изображен на рис. 35.
у
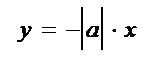
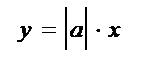
О х Рис. 35
Свойства функции 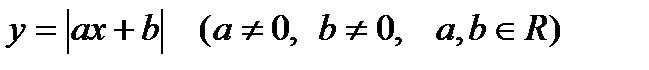
1) 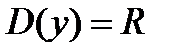 ;
;
2) 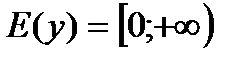 ;
;
3) Функция является функцией общего вида;
4) Функция не является периодической;
5) Функция имеет один корень: 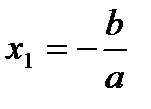 . График функции касается оси Ох в точке
. График функции касается оси Ох в точке  ;
;
6) Функция положительна на промежутках  и
и  . В точке
. В точке  обращается в нуль;
обращается в нуль;
7) График функции пересекает ось Оу в точке 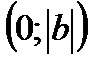 ;
;
8) Функция убывает на промежутке  , возрастает на
, возрастает на  ;
;
9) Функция имеет минимум в точке  , причем
, причем  ;
;
10) Графики функции изображены на рис. 36–37.
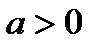 ,
, 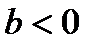
у
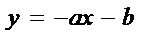
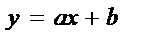
О  х Рис. 36
х Рис. 36
 ,
, 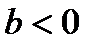
у
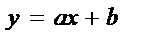
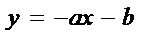
 О х Рис. 37
О х Рис. 37
7. ДРОБНО–ЛИНЕЙНАЯ ФУНКЦИЯ 
1) 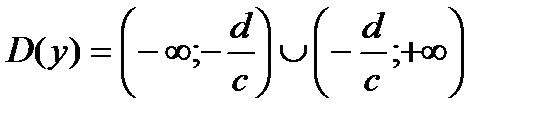 ;
;
2)  ;
;
3) Функция является функцией общего вида;
4) Функция не является периодической;
5) При 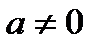 функция имеет один корень:
функция имеет один корень: 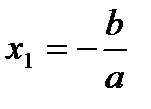 . В этом случае график функции пересекает ось Ох в точке
. В этом случае график функции пересекает ось Ох в точке  . При
. При  функция не имеет корней и график функции не пересекает ось Ох;
функция не имеет корней и график функции не пересекает ось Ох;
6) При 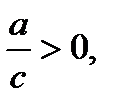
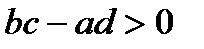 функция положительна на
функция положительна на 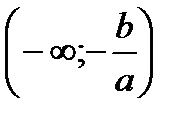 и
и 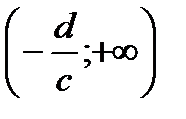 , отрицательна на
, отрицательна на  . При
. При 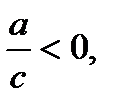
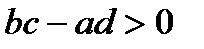 функция положительна на
функция положительна на 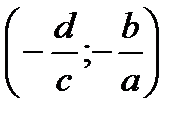 , отрицательна на
, отрицательна на 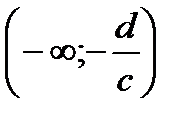 и
и 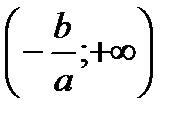 ; При
; При 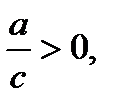
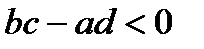 функция положительна на промежутках
функция положительна на промежутках  и
и 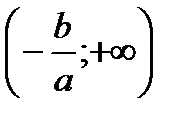 , отрицательна на
, отрицательна на 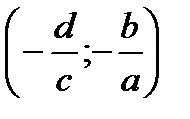 . При
. При 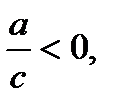
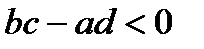 функция положительна на промежутке
функция положительна на промежутке  , отрицательна на промежутках
, отрицательна на промежутках 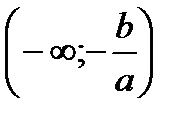 и
и 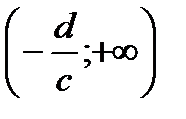 ;
;
7) При  график функции пересекает ось Оу в точке
график функции пересекает ось Оу в точке 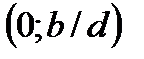 . При
. При 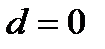 график функции не пересекает ось Оу;
график функции не пересекает ось Оу;
8) При 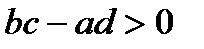 функция убывает на
функция убывает на 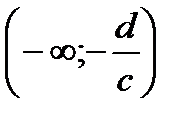 и
и 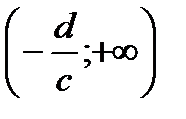 .
.
При 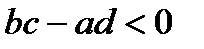 функция возрастает на
функция возрастает на 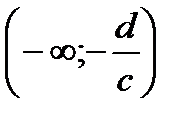 и
и 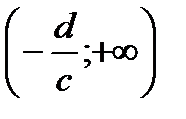 ;
;
9) Функция не имеет экстремумов;
10) Графики функции изображены на рис.38–1.
у 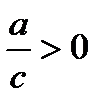 ,
, 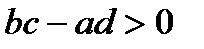
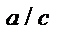
О 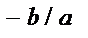
 х
х
Рис. 38
у  ,
, 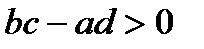
О 
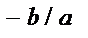 х
х
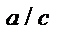
Рис. 39
у 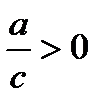 ,
, 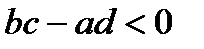
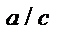
О 
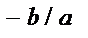 х
х
Рис. 40
у  ,
, 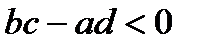
О 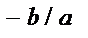
 х
х
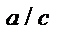
Рис. 41