ТЕМА: “ Теорема о сумме углов треугольника и ее следствие о внешнем угле треугольника.”
Цели урока: организовать деятельность учащихся по восприятию теоремы о сумме углов треугольника, ее доказательству, осмыслению и применению в решении задач.
ХОД УРОКА:
1. Орг. момент
На предыдущих уроках мы с вами изучали признаки и свойства параллельности прямых. И сегодня на уроке, полученные по этой теме знания, помогут сделать открытие, Фигура, с которой мы будем работать, вам уже знакома. Это треугольник. (слайд 2)
2. (мотивация) Треугольник в геометрии играет особую роль. Без преувеличения можно сказать, что вся или почти вся геометрия строится на треугольнике. За несколько тысячелетий геометры столь подробно изучили треугольник,что иногда говорят о геометрии треугольника как о самостоятельном разделе геометрии.
Что мы о нем знаем? Сколько у треугольника вершин, углов, сторон? Какие треугольники вы знаете? Слайд 3. Как их можно классифицировать, если различать по сторонам: равносторонние, равнобедренные, произвольные (разносторонние или треугольники общего вида).
3. (актуализация) На дом к сегодняшнему уроку вам было задано построить 3 разных треугольника, измерить углы в каждом треугольнике и вычислить сумму углов каждого треугольника. Какие значения суммы вы получили? Чем объясняется небольшое различие? Тем ли что нет никакой закономерности, или тем, что закономерность есть, но нашими инструментами мы не можем установить её с достаточной точностью? К какому числу близки эти значения? К 1800. Кто-то из учеников скажет, что мы ведь уже учили в 5 классе, что сумма углов треугольника равна 1800. Да, но как мы убеждались в верности данного утверждения? Только путем измерений. Но, теперь, изучая геометрию, мы должны опираться на доказательства утверждений, кажущихся нам верными. Поэтому, какова тема нашего урока? Ученики сами формулируют «Сумма углов треугольника». А что мы будем на уроке делать? Во – первых, постараемся доказать теорему о сумме углов треугольника, во-вторых посмотрим как и где она применяется в задачах. Открыли тетради, записали число, тема урока: Сумма углов треугольника.
4. (Организация восприятия)
Теорема: сумма углов треугольника равна 180°.
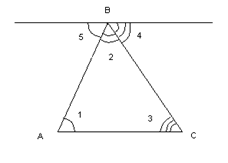Дано: ΔАВС – произвольный
Доказать: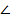 
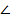А + В + 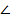С = 180º
Для доказательства записать на доске дано, док-ть, рисунок. Провести подсказку - прямую а. дать время на обдумывание, спросить варианты доказательства, вызвать ученика для записи доказательства.
Доказательство:
1. проведем а 
АС
2. по свойству №1 параллельных прямых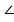 
5 = 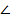1 (накрест лежащие),
3. 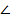4 = 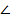3 (накрест лежащие)
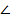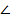4. 5 + 2 + 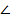4 = 180º (развернутый угол)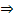 
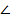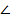1 + 2 + 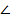3 = 180º ч. т. д.
5. Устная работа (организация осмысления) С лайды 4,5.
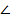А =50°, 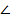В =70°
Слайд 6. Чему равен угол равностороннего треугольника? (60º)
Чему равна сумма острых углов прямоугольного треугольника? (90º)
Слайд 7. Может ли быть в треугольнике три острых угла?(+)
А три тупых угла? (-)Два тупых угла? (-)Три прямых угла? (-)Два прямых угла?(-)
Может ли быть в треугольнике один прямой угол, а один тупой?(-)
Из этого можно сделать вывод, который является следствием из теоремы:
Слайд 8. В любом треугольнике либо все углы острые, либо два угла острые, а третий или прямой или тупой.
6. Изобразите три угла: острый, прямой и тупой. Достройте каждый из них до треугольника. Подпишите, как называются эти треугольники: остроугольный, прямоугольный, тупоугольный. Итак, мы теперь можем классифицировать треугольники по углам.
7. Рассмотрим и заполним вместе таблицу: классификация треугольников.
Слайд 9-11
| По углам | По сторонам | ||
| произвольный | равнобедренный | равносторонний | |
| Остроугольный | |||
| Прямоугольный | - | ||
| Тупоугольный | - |
8. Первичная проверка понимания. №224, 228(в)
№224. Пусть х-одна часть, тогда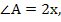 
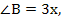
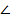С=4х. по теореме о сумме углов треугольника 2х+3х+4х=180°. 9х=180°, х=20°.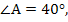 
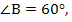
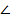С=80°.
№228(в). Угол 100° в равнобедренном треугольнике может быть только при вершине. 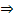сумма острых равных углов при основании равна80°. Каждый по 40°.
9. На слайде 12-13. Устная работа (организация первичного закрепления)
Решают самостоятельно. Опрос ответов. Выяснение причин неверных ответов
10. Итоги:
Что мы сегодня новое узнали? Что подтвердили доказательством? Какие следствия из теоремы получили? Как мы можем теперь классифицировать треугольники?
11. Д.з. п.30-31, №223(г), №228(а) прокомментировать то, что может быть два решения.