ЗАДАНИЕ 1. ОДНОКРАТНОЕ ИЗМЕРЕНИЕ
Условие задания
При однократном измерении физической величины получено показание средства измерения X = 10. Определить, чему равно значение измеряемой величины, если экспериментатор обладает априорной информацией о средстве измерений и условиях выполнения измерений согласно данным таблицы 1.
Указания по выполнению
1. Исходные данные студент выбирает из таблицы 1 по предпоследней и последней цифрам шифра; например шифру 96836 соответствует априорная информация, определяемая на пересечении строки 3и столбца 6.
2. Априорная информация в таблице 1 представлена в двух вариантах. В первом варианте даются сведения о классе точности средства измерений: пределы измерений, класс точности, значение аддитивной (θа) или мультипликативной (θМ) поправки. Например, данные: -50...50; 1,5; θа = 0,5 - означают, что средство измерения имеет диапазон измерений от -50 до 50, класс точности 1,5, а значение аддитивной поправки равняется 0,5.
Во втором варианте в качестве априорной информации даются сведения о видах и характеристиках распределения информации результата измерения: вид закона распределения, значение оценки среднего квадратического отклонения (Sx), доверительная вероятность Р (для нормального закона распределения) и значение аддитивной (θа) или мультипликативной (θМ) поправки. Например, данные: норм.; Sx =0,5; Р = 0,95; θМ= 1,1 - означают, что закон распределения вероятности результата измерения нормальный со значением оценки среднеквадратического отклонения 0,5. При этом имеет место мультипликативная поправка (поправочный множитель) 1,1, а доверительный интервал следует рассчитывать с доверительной вероятностью 0,95.
Порядок расчета
Результат измерения при однократном измерении определяется по алгоритму, представленному на рисунке 34 [1].
Обработка экспериментальных данных зависит от вида используемой априорной информации. Если это информация о классе точности, то пределы, в которых находится значение измеряемой величины без учета поправки, определяются следующим образом:

где 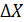 - предел допускаемой абсолютной погрешности средства измерения при его показании X. Значение
- предел допускаемой абсолютной погрешности средства измерения при его показании X. Значение 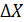 определяется в зависимости от класса точности и способа его задания по ГОСТ 8.401-80.
определяется в зависимости от класса точности и способа его задания по ГОСТ 8.401-80.
Если в качестве априорной используется информация о законе распределения вероятности, то пределы определяются через доверительный интервал:

Значение Е определяется в зависимости от вида закона распределения вероятности результата измерения. Для нормального закона
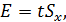
где t для заданной доверительной вероятности Р выбирается из таблиц интегральной функции нормированного нормального распределения Ф(t) (например, табл. 1.1.2.6.2 [2], при этом следует учитывать, что Р = 2Ф(t)). Таблица распределения также приведена в приложении Б.
Для равномерного закона распределения вероятности результата измерения значение Е (аналог доверительного интервала) можно определить из выражения
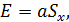
где 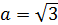 .
.
При представлении результата измерения необходимо внести поправки и уточнить пределы, в которых находится значение измеряемой величины.
При вычислении следует руководствоваться правилами округления, согласно которым значения среднеквадратических отклонений указываются в окончательном ответе двумя значащими цифрами, если первая из них равна 1 или 2, и одной, если первая равна 3 или более. Все предварительные расчеты выполняются не менее чем с одним или двумя лишними знаками.
В качестве справочных данных могут использоваться аналогичные таблицы из других литературных источников.
ЗАДАНИЕ 2. МНОГОКРАТНОЕ ИЗМЕРЕНИЕ
Условие задания
При многократном измерении одной и той же физической величины получена серия из 24 результатов измерений 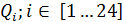 . Эти результаты после внесения поправок представлены в таблице 2. Определить результат измерения.
. Эти результаты после внесения поправок представлены в таблице 2. Определить результат измерения.
| Предпоследняя цифра шифра | Последняя цифра шифра | ||||||||||
| 482 495 | |||||||||||
| 492 484 | |||||||||||
| 483 494 | |||||||||||
| 492 486 | |||||||||||
| 481 494 | |||||||||||
| 495 484 | |||||||||||
| 485 492 | |||||||||||
| 492 483 | |||||||||||
| 482 493 | |||||||||||
| 493 480 | |||||||||||
| 492 484 | 487 495 | 492 484 | 483 495 | 493 484 | 487 495 | 493 484 | 485 492 | 492 484 |