1. 1)  ; 2)
; 2)  ; 3)
; 3)  ; 4)
; 4)  ; 5)
; 5) 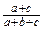 ; 6)
; 6)  . 2. 0,4. 3.
. 2. 0,4. 3.  . 4.
. 4. 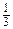 . 5.
. 5.  . 6. 1)
. 6. 1) 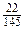 ; 2)
; 2) 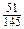 ; 3)
; 3)  . 7. 0,375. 8.
. 7. 0,375. 8.  . 9.
. 9.  . 10.
. 10.  . 11.
. 11.  . 12. 15. 13. Первый – 114 изделий, второй – 112 изделий. 14.
. 12. 15. 13. Первый – 114 изделий, второй – 112 изделий. 14.  . 15.
. 15. 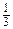 .
.
*Схема Бернулли. Формула Пуассона.
Локальная и интегральная теоремы Муавра–Лапласа [21]
1. 1)  ; 2)
; 2)  . 2. От 59 до 65 раз включительно. 3. 0,1755. 4. 1)
. 2. От 59 до 65 раз включительно. 3. 0,1755. 4. 1)  ; 2)
; 2)  ; 3)
; 3)  . 5. 1)
. 5. 1)  ; 2) а)
; 2) а)  ; б)
; б)  ; в)
; в) 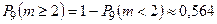 ; 3)
; 3) 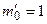 ,
, 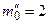 . 6. 1) а)
. 6. 1) а) 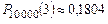 ; б)
; б)  ; 2) а) событие «не будет повреждено 9 997 изделий из 10 000» равносильно событию «будет повреждено три изделия из 10 000», следовательно, их вероятности равны (см. ответ 1) а)); б) событие «не будет повреждено хотя бы 9 997 изделий из 10 000» равносильно событию «будет повреждено не более трех изделий из 10 000», тогда
; 2) а) событие «не будет повреждено 9 997 изделий из 10 000» равносильно событию «будет повреждено три изделия из 10 000», следовательно, их вероятности равны (см. ответ 1) а)); б) событие «не будет повреждено хотя бы 9 997 изделий из 10 000» равносильно событию «будет повреждено не более трех изделий из 10 000», тогда  . 7. а)
. 7. а) 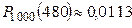 ; б)
; б)  ; в)
; в)  ; г)
; г)  . 8. Решение. Размер прибыли компании составляет разность между суммарным взносом всех клиентов и суммарной страховой суммой, выплаченной
. 8. Решение. Размер прибыли компании составляет разность между суммарным взносом всех клиентов и суммарной страховой суммой, выплаченной  клиентам при наступлении страхового случая, то есть
клиентам при наступлении страхового случая, то есть  тыс. руб. Для определения
тыс. руб. Для определения  применим интегральную теорему Муавра–Лапласа (требование
применим интегральную теорему Муавра–Лапласа (требование  выполнено). По условию задачи
выполнено). По условию задачи  , где
, где  – число клиентов, которым будет выплачена страховая сумма,
– число клиентов, которым будет выплачена страховая сумма,  ,
,  . Из последнего соотношения выразим
. Из последнего соотношения выразим  :
: 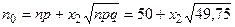 . Из уравнения
. Из уравнения  найдем
найдем  :
: 
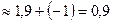 . Тогда
. Тогда  (Приложение 3). Следовательно,
(Приложение 3). Следовательно,  ,
,  тыс. руб.
тыс. руб.
Тема 25
Задания для решения на практическом занятии
1. 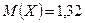 ,
, 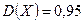 ,
, 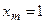 . 2.
. 2. 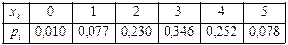 ,
,  ,
,  . 3.
. 3.  . 4.
. 4.  . 5. Ряд распределения
. 5. Ряд распределения 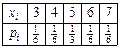 , функция распределения
, функция распределения  . 6. 0,000055. 7. 0,09. 8. 0,13534. 9.
. 6. 0,000055. 7. 0,09. 8. 0,13534. 9. 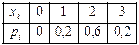 .
.
Задания для самостоятельной работы
1.  ,
, 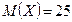 ,
,  ,
, 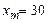 . 2.
. 2.  ,
, 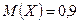 . 3.
. 3.  .
.
4.  ,
,  ,
, 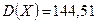 ,
,  . 5. 0,000004. 6. Ряд распределения
. 5. 0,000004. 6. Ряд распределения  . Функция распределения
. Функция распределения  . 7.
. 7.  ,
,  . 8.
. 8. 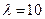 ,
,  . 9.
. 9.  .
.
Тема 26
Задания для решения на практическом занятии
1. 1)  ; 2) графиком плотности распределения на отрезке
; 2) графиком плотности распределения на отрезке  является парабола
является парабола  , а вне этого отрезка – прямая
, а вне этого отрезка – прямая  ; 3)
; 3)  . 2.
. 2. 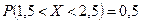 ,
,  ,
, 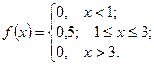 3.
3.  ,
, 
 ,
, 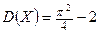 ,
,  . 4.
. 4. 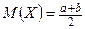 ,
,  ,
, 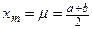 . 5.
. 5.  ,
,  ,
,  ,
,  ,
,  6.
6.  . 7.
. 7.  ,
,  ,
,  ,
, 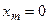 ,
,  . 8. 1)
. 8. 1)  ; 2)
; 2)  . 9.
. 9.  . 10. Точность
. 10. Точность  . 11. 0,096. 12. 0,8533.
. 11. 0,096. 12. 0,8533.
Задания для самостоятельной работы
1. 1)  ; 2) графиком плотности распределения на отрезке
; 2) графиком плотности распределения на отрезке 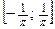 является функция
является функция 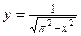 , а вне этого отрезка – прямая
, а вне этого отрезка – прямая  ; 3)
; 3)  . 2.
. 2.  ,
,  ,
,  3.
3. 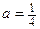 ,
, 
 ,
,  ,
,  ;
;  . 4.
. 4.  ,
,  ,
,  ,
,  ,
,  . 5. 0,2231. 6. 0,424. 7. 0,9876. 8. 0,018.
. 5. 0,2231. 6. 0,424. 7. 0,9876. 8. 0,018.
ПРИЛОЖЕНИЯ
Приложение 1
Кривые второго порядка
| Название, каноническое уравнение | Чертеж | Элементы |
Эллипс

| 
|  – большая ось, – большая ось, 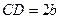 – малая ось; – малая ось;  , ,  , , 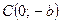 , , 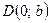 – вершины; – вершины;  – центр; – центр;  , ,  – фокусы; – фокусы;  ( ( ) – эксцентриситет; ) – эксцентриситет;  ; ;
 – площадь эллипса – площадь эллипса
|
Окружность с центром в начале координат 
| 
|  – центр; – центр; 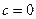 ; ; 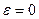 – эксцентриситет, – эксцентриситет,  – радиус – радиус
|
Окружность с центром в точке 
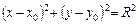
| 
|  – центр; – центр;  ; ;
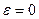 – эксцентриситет, – эксцентриситет, 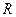 – радиус – радиус
|
Гипербола

| 
|  – действительная ось, – действительная ось, 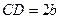 – мнимая ось; – мнимая ось;
 , ,  – вершины; – вершины;
 – центр; – центр;  ; ;
 , ,  – фокусы; – фокусы;
 ( (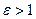 ) – эксцентриситет; ) – эксцентриситет;
 – асимптоты – асимптоты
|
Равнобочная гипербола

| 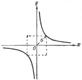
|  ; асимптоты (оси координат) перпендикулярны ; асимптоты (оси координат) перпендикулярны
|
Парабола

| 
|  – ось параболы; – ось параболы;  – фокус; – фокус;
 – вершина параболы; – вершина параболы;
 – эксцентриситет; – эксцентриситет;
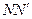 ( ( ) – директриса гиперболы ) – директриса гиперболы
|
Парабола с вертикальной осью 
| 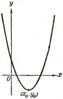
|  – вершина параболы; – вершина параболы;
 , ,  ; ;
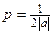
|
Приложение 2
Поверхности второго порядка
| Название, каноническое уравнение, элементы | Чертеж | Линии уровня |
Эллипсоид
 ; ; 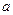 , ,  , ,  – полуоси; при – полуоси; при  – сфера. – сфера.
| 
| При сечении плоскостью  ( ( ) – эллипсы ) – эллипсы  , ,  . При сечении плоскостью . При сечении плоскостью  ( ( ) – эллипсы ) – эллипсы  , ,  . При сечении плоскостью . При сечении плоскостью  ( ( ) – эллипсы ) – эллипсы  , , 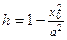
|
Однополостный гиперболоид
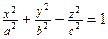 ; ; 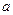 , ,  – действительные полуоси, – действительные полуоси,  – мнимая полуось. – мнимая полуось.
| 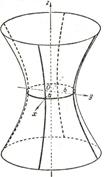
| При сечении плоскостью  – эллипсы – эллипсы  , ,  . При сечении плоскостью . При сечении плоскостью  – гиперболы – гиперболы 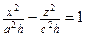 , ,  . При сечении плоскостью . При сечении плоскостью  – гиперболы – гиперболы  , , 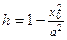
|
Двуполостный гиперболоид
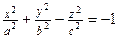 ; ; 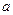 , ,  – мнимые полуоси, – мнимые полуоси,  – действительная полуось. – действительная полуось.
| 
| При сечении плоскостью  ( (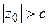 ) – эллипсы ) – эллипсы 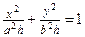 , ,  . При сечении плоскостью . При сечении плоскостью 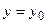 – гиперболы – гиперболы  , ,  . При сечении плоскостью . При сечении плоскостью  – гиперболы – гиперболы  , , 
|
Конус
 ; ;  – вершина конуса. – вершина конуса.
| 
| При сечении плоскостью  ( (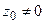 ) – эллипсы ) – эллипсы 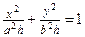 , ,  . При сечении плоскостью . При сечении плоскостью 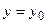 ( ( ) – гиперболы ) – гиперболы 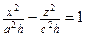 , , 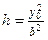 . При сечении плоскостью . При сечении плоскостью  ( (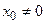 ) – гиперболы ) – гиперболы  , ,  . При сечении плоскостью . При сечении плоскостью  – прямые – прямые 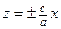 . При сечении плоскостью . При сечении плоскостью  – прямые – прямые 
|
Окончание приложения 2
| Название, каноническое уравнение, элементы | Чертеж | Линии уровня |
Эллиптический параболоид
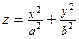 ; ;  – вершина эллиптического параболоида. – вершина эллиптического параболоида.
| 
| При сечении плоскостью  ( ( ) – эллипсы ) – эллипсы 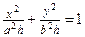 , ,  . При сечении плоскостью . При сечении плоскостью  – параболы – параболы 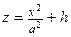 , , 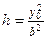 . При сечении плоскостью . При сечении плоскостью  – параболы – параболы  , , 
|
Гиперболический параболоид
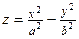 ; ;  – вершина гиперболического параболоида. – вершина гиперболического параболоида.
| 
| При сечении плоскостью  ( ( ) – гиперболы ) – гиперболы  , ,  . При сечении плоскостью . При сечении плоскостью  – параболы – параболы  , , 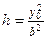 . При сечении плоскостью . При сечении плоскостью  – параболы – параболы  , ,  . При сечении плоскостью . При сечении плоскостью  – прямые – прямые 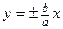
|
Эллиптический цилиндр

| 
| При сечении плоскостью  – эллипсы – эллипсы 
|
Гиперболический цилиндр

| 
| При сечении плоскостью  – гиперболы – гиперболы 
|
Параболический цилиндр

| 
| При сечении плоскостью  – параболы – параболы 
|
Приложение 3
Элементарные функции
| № п/п | Обозначение | Область определения | Область значений | Монотонность | Свойства | График |
| Степенная функция | ||||||
| 1. | 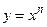 
| 
|  , если , если  нечетно нечетно
| возрастает на  , если , если  нечетно нечетно
| нечетная, если  – нечетно, непериодическая – нечетно, непериодическая
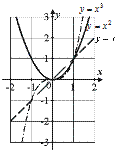
| 
|
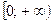 , если , если  – четно – четно
| убывает на  , возрастает на , возрастает на  , если , если  четно четно
| четная, если  – четно, непериодическая – четно, непериодическая
| ||||
| 2. | 
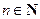
| 
|  если
если  – нечетно – нечетно
| убывает на  и на и на  , если , если  – нечетно – нечетно
| нечетная, если  – нечетно, непериодическая – нечетно, непериодическая
| 
|
 , если , если  – четно – четно
| возрастает на  и убывает на и убывает на  , если , если  – четно – четно
| четная, если  – четно, непериодическая – четно, непериодическая
| 
| |||
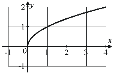
| 3. | 
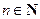

|  , если , если  – нечетно – нечетно
|  , если , если  – нечетно – нечетно
| возрастает на интервале  , если , если  – нечетно – нечетно
| нечетная, если  – нечетно, непериодическая – нечетно, непериодическая
| 
|
 , если , если  – четно – четно
| 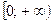 , если , если  – четно – четно
| возрастает на  , если , если  – четно – четно
| ни четная, ни нечетная, если  – четно, непериодическая – четно, непериодическая
| 
| ||
| Показательная функция | ||||||
| 4. |   , , 
| 
| 
| возрастает на  , если , если 
| не является ни четной, ни нечетной, непериодическая | 
|
убывает на  , если , если 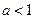
| ||||||
| Логарифмическая функция | ||||||
| 5. |   , , 
| 
| 
| возрастает на  , если , если 
| не является ни четной, ни нечетной, непериодическая | 
|
убывает на  , если , если 
|
Окончание приложения 3
| Тригонометрические функции | ||||||
| 6. | 
| 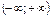
| 
| возрастает на  , убывает на , убывает на  , , 
| нечетная, периодическая с периодом 
| 
|
| 7. | 
| 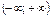
| 
| возрастает на 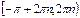 , убывает на , убывает на  , , 
| четная, периодическая с периодом 
| 
|
| 8. | 
| 
| 
| возрастает на  , , 
| нечетная, периодическая с периодом 
| 
|
| 9. | 
| 
| 
| убывает на  , , 
| периодическая с периодом  , нечетная , нечетная
| 
|
| Обратные тригонометрические функции | ||||||
| 10. | 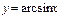
| 
| 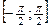
| возрастает на 
| нечетная, непериодическая | 
|
| 11. | 
| 
| 
| убывает на 
| не является ни четной, ни нечетной, непериодическая | |
| 12. | 
| 
| 
| возрастает на 
| нечетная, непериодическая |

|
| 13. | 
| 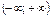
| 
| убывает на 
| не является ни четной, ни нечетной, непериодическая |

|
Приложение 4
Таблица значений функции Гаусса

| 7 | ||||||||||
| 0,0 | 0,3989 | |||||||||
| 0,1 | ||||||||||
| 0,2 | ||||||||||
| 0,3 | ||||||||||
| 0,4 | ||||||||||
| 0,5 | ||||||||||
| 0,6 | ||||||||||
| 0,7 | ||||||||||
| 0,8 | ||||||||||
| 0,9 | ||||||||||
| 1,0 | 0,2420 | |||||||||
| 1,1 | ||||||||||
| 1,2 | ||||||||||
| 1,3 | ||||||||||
| 1,4 | ||||||||||
| 1,5 | ||||||||||
| 1,6 | ||||||||||
| 1,7 | ||||||||||
| 1,8 | ||||||||||
| 1,9 | ||||||||||
| 2,0 | 0,0540 | |||||||||
| 2,1 | ||||||||||
| 2,2 | ||||||||||
| 2,3 | ||||||||||
| 2,4 | ||||||||||
| 2,5 | ||||||||||
| 2,6 | ||||||||||
| 2,7 | ||||||||||
| 2,8 | ||||||||||
| 2,9 | ||||||||||
| 3,0 | 0,0044 | |||||||||
| 3,1 | ||||||||||
| 3,2 | ||||||||||
| 3,3 | ||||||||||
| 3,4 | ||||||||||
| 3,5 | ||||||||||
| 3,6 | ||||||||||
| 3,7 | ||||||||||
| 3,8 | ||||||||||
| 3,9 |