Ограниченный тип (диапазон)

Через диапазон можно определить тип, который будет содержать зна­чения только из ограниченного поддиапазона некоторого базового типа. Базовым типом может быть любой целочисленный тип, тип CHAR или любой из введенных программистом перечислимых типов. Определяется тип-диапазон в разделе TYPE указанием имени типа и границ диапазона, разделенных двумя точками:

TYPE < ИмяДиапазона > = < НачальноеЗначение >.. < КонечноеЗначение >;

Начальное значение при определении такого типа не должно быть больше конечного.

Пример: TYPE

TEST1 = (test1, test2, ...,test5);

H= 1 .. 20; {поддиапазон для типа Integer}

LETERS = 'A' .. 'Я'; {базовый тип Char}

TESTOD = test2 .. test5; {базовый тип TEST1}

Определение переменных для диапазона производится в разделе VAR. Они могут принимать любые значения из указанного диапазона, включая граничные.

При конструировании диапазона в описании типа можно использовать несложные арифметические выражения для вычисления границ. Но при этом надо следить, чтобы запись выражения не начиналась со скобки (скобка - это признак начала перечисления).

Пример:

CONST N = 30;

TYPE date = 1..31;

kv2 = 3*N+1..6*N;

VAR L, L1: date;

k: kv2;

BEGIN

L:=2*10+5;...

L1:=2*10+60; {неверно, т.к. L1 выходит за пределы диапазона}

END.

Применение ограниченных типов усиливает контроль данных при вы­полнении программы. Значения переменных типа «диапазон» могут выводить­ся на экран и вводиться с клавиатуры только в том случае, когда диапа­зон взят из базового стандартного типа.

Пример и задания для двумерных массивов

Пример. Вычислить суммы элементов в столбцах двумерного числового массива А размером [1..3,1..4].

Текст программы для СА (рис. 13):

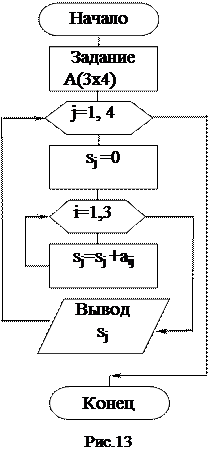Program lr7_1;

CONST a: array[1..3,1..4] of integer =

((1,2,3,4),(1,2,3,4),(1,2,3,4));

VAR

i, j: integer;

s: array[1..4] of integer; {массив сумм}

BEGIN

for j:= 1 to 4 do

begin

s[j]:= 0;

for I:= 1 to 3 do

s[j]:= s[j] + a[i,j];

write(' s[', j, ']=', s[j])

end

END.

Задания для самостоятельного выполнения

Задание 1

1. Даны матрицы A,B: array [1..4,1..4] of real. Вычислить матрицу С поэлементным сложением соответствующих элементов матриц А и В.

2. Дана матрица B: array [1..5,1..5] of real. Найти для нее транспонированную.

3. Даны матрица A: array[1..4,1..4], содержащая вещественные числа, и константа k. Вычис­лить матрицу С = k *А.

4. Сформировать массив по правилу 1 0 0... 0

2 1 0... 0

3 2 1... 0

...

10 9 8... 1

5. Даны натуральное N и элементы а _ij квадратной вещественной матрицы А пятого порядка. Вычислить N-ю степень каждого элемента этой матрицы по схеме (а _ij¹ = а _ij, а _ij² = а _ij* а _ij, а _ij³ = а _ij²* а _ij и т.д., где i, j = 1, 2,..., 5).

6. Сформировать массив по правилу 0 0 0...0

0 1 0...0

0 0 2...0.

…

0 0 0...9

7. Сформировать массив последовательностью натуральных чисел:

1 2... 10

11 12... 20

21 22... 30.

...

91 92... 100

 

8. Сформировать двумерный массив: 1 2 3 4 5

5 1 2 3 4

4 5 1 2 3.

3 4 5 1 2

2 3 4 5 1

9. Дана матрица A: array [1..N,1..N] of integer. Сформировать век­тор В из максимальных элементов каждой строки.

10. Дана матрица A: array [1..6,1..6] of integer и переменная x. Элементы нечетных строк матрицы А заменить на значение x.

11. Дана матрица B: array [1..5,1..5]. Получить массив С удалением (либо обнулением) n-й строки и k-го столбца из матрицы В.

12. Определить, является ли заданная квадратная матрица девятого порядка магическим квадратом, т.е. такой, в которой суммы элементов во всех строках и столбцах будут одинаковы.

13. Определить, является ли заданная целая квадратная матрица шестого порядка симметричной (относительно главной диагонали).

14. Дана вещественная матрица A: array [1..7,1..4]. Переставляя ее строки и столбцы, добиться того, чтобы наибольший элемент оказался в верхнем левом углу.

15. Дана вещественная матрица размером 4х8. Упорядочить ее стро­ки по не- убыванию сумм их элементов.

16. Для заданной целой матрицы размером 6х8 элементов напечатать индексы всех ее седловых точек. Элемент матрицы называется седловой точкой, если он является наименьшим в своей строке и одновременно на­ибольшим в своем столбце или, наоборот, является наибольшим в своей строке и наименьшим в своем столбце.

17. Дана матрица A: array [1..6,1..2] вещественных чисел. Рассмат­ривая A [i,1] и A [i,2] как координаты точек на плоскости, определить радиус наименьшего круга (с центром в начале координат), внутрь кото­рого попадают все эти точки.

18. Дан массив F: array [1..N,1..M] of byte. Определить количество «особых» элементов в нем. Элемент считается «особым», если он больше суммы остальных элементов своего столбца.

19. Дана матрица D: array [1..5,1..6] of integer. Упорядочить эле­менты строк в нем по убыванию.

20. Дан массив М координат точек на плоскости. Найти наибольшее расстояние между этими точками.

Задание 2

Сформировать таблицу Пифагора для чисел натурального ряда.

Задание 3

Модифицировать программу_3_2 (или 6_3) таким образом, чтобы значения X, F1 и F2 были представлены двумерным массивом, состоящим из трех строк.