Признаки параллелограмма.

Справочный материал по геометрии

Параллелограмм:

Cвойства параллелограмма:

1. Противоположные стороны параллелограмма равны: AB = CD, AD = DC
2. Противоположные углы параллелограмма равны: ∠A=∠C,∠B=∠D 3. Сумма углов параллелограмма, прилежащих к одной его стороне составляет 180°.Например, ∠A+∠B = 180°
4. Любая диагональ параллелограмма делит его на два равных треугольника.Δ ABD = Δ BCD
5. Диагонали параллелограмма пересекаются и точкой пересечения делятся пополам.AO = OC, BO = OD
6. Пусть АС = d1 и BD = d2, ∠COD = α, тогда - сумма квадратов диагоналей параллелограмма равна сумме квадратов всех его сторон (d1)2 + (d2)2 = 2a2 + 2b2
7. Площадь параллелограмма:1) S = ah; 2) S = ab∙sinα; 3) S = (½) d1∙d2∙sinβ

Признаки параллелограмма.

· Если две противоположные стороны четырехугольника параллельны и равны, то этот четырехугольник — параллелограмм.

· Если противоположные стороны четырехугольника попарно равны, то этот четырехугольник — параллелограмм.

· Если диагонали четырехугольника пересекаются и точкой пересечения делятся пополам, то этот четырехугольник — параллелограмм.

Прямоугольник: Прямоугольник — это параллелограмм, у которого все углы прямые.

Cвойства прямоугольника:

1. Прямоугольник обладает всеми свойствами параллелограмма
2. Диагонали прямоугольника равны. AC = BD
3. Площадь прямоугольника можно найти по формулам: 1) S = a ∙ b; 2) S = (½)· d² ∙ sinα; (где a и b – стороны, d- диагональ прямоугольника, α = ∠COD – угол между диагоналями)
4. Около любого прямоугольника можно описать окружность, центр которой – точка пересечения диагоналей; диагонали являются диаметрами описанной окружности.

Ромб: Ромб — это параллелограмм, у которого все стороны равны.

Cвойства ромба:

1. Ромб обладает всеми свойствами параллелограмма
2. Диагонали ромба взаимно перпендикулярны. AC | BD
3. Диагонали ромба являются биссектрисами его углов.
4. Площадь ромба:1) S = ah; 2) S = a2∙sinα; 3) S = (½) d1∙d2; 4) S = P ∙ r, где P – периметр ромба, r – радиус вписанной окружности

Квадрат:

Все стороны квадрата равны, диагонали квадрата равны и пересекаются под прямым углом. Диагональ квадрата d=a√2 Площадь квадрата:1) S = a2; 2) S = (½) d2

Трапеция:

· Основания трапеции AD||BC, MN-средняя линия, MN = (AD+BC)/2. · Отрезок, соединяющий середины диагоналей трапеции, равен полуразности оснований. · Точка пересечения диагоналей трапеции, точка пересечения продолжения боковых сторон и середины оснований трапеции – лежат на одной прямой. (Другими словами: если соединить точку пересечения диагоналей с точкой пересечения боковых сторон трапеции, то эта прямая пройдет через середины оснований трапеции).

· Площадь трапеции равна произведению полусуммы ее оснований на высоту: S = (AD+BC) ∙ BF /2 или S = (a+b)∙h/2. · В равнобедренной (равнобокой) трапеции длины боковых сторон равны; углы при основании равны; диагонали равны.

Площадь любого четырехугольника:

• равна половине произведения его диагоналей на синус угла между ними: S = (½) d₁∙d₂∙sinβ.

• равна половине произведения его периметра на радиус вписанной окружности: S = (½) P∙r.

Вписанные и описанные четырехугольники:

1. В выпуклом четырехугольнике, вписанном в окружность, произведение диагоналей равно сумме произведений противоположных сторон (теорема Птолемея): AC∙BD=AB∙DC+AD∙BC
2. Если суммы противолежащих углов четырехугольника равны по 180°, то около четырехугольника можно описать окружность. Обратное утверждение также верно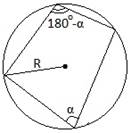
3. Если суммы противолежащих сторон четырехугольника равны (a + c = b + d), то в этот четырехугольник можно вписать окружность. Обратное утверждение также верно

Окружность, круг:

1) Длина окружности С = 2πr; 2) Площадь круга S=πr2; 3) Длина дуги АВ: 4) Площадь сектора АОВ: 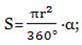5) ∠AOB = α – центральный угол. Градусная мера дуги l равна α градусов.

Прямоугольный треугольник:

1. Теорема Пифагора: В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов: c²=a²+b²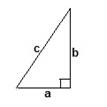
2. Площадь прямоугольного треугольника: SΔ=(½) a∙b, где a и b — катеты илиSΔ=(½) c∙h, где с — гипотенуза, h –высота, проведенная к гипотенузе
3. Радиус вписанной в прямоугольный треугольник окружности: r = (a + b - c) / 2
4. Радиус описанной около прямоугольного треугольника окружностиравен половине гипотенузы: R = АВ/2.   Медиана прямоугольного треугольника, проведенная к гипотенузе, равна половине гипотенузы (это радиус описанной окружности) OC=OC1=R
5. Пропорциональные отрезки в прямоугольном треугольнике: Высота, проведенная из вершины прямого угла к гипотенузе есть средняя пропорциональная величина между проекциями катетов на гипотенузу: h2=ac∙bc; а каждый катет есть средняя пропорциональная величина между всей гипотенузой и проекцией данного катета на гипотенузу: a2=c∙ac и b2=c∙bc
6. Синусом углапрямоугольного треугольника называется отношение противолежащего катета к гипотенузе. Косинусом углапрямоугольного треугольника называется отношение прилежащего катета к гипотенузе. Тангенсом углапрямоугольного треугольника называется отношение противолежащего катета к прилежащему катету. Котангенсом углапрямоугольного треугольника называется отношение прилежащего катета к противолежащему катету.

Теорема синусов: В любом треугольнике стороны пропорциональны синусам противолежащих углов
Следствие из теоремы синусов: Каждое из отношений стороны к синусу противолежащего угла равно 2R, где R — радиус окружности, описанной около треугольника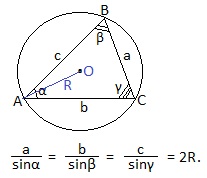

Теорема косинусов: Квадрат любой стороны треугольника равен сумме квадратов двух других ее сторон без удвоенного произведения этих сторон на косинус угла между ними

Треугольники:

1. Свойства равнобедренного треугольника:В равнобедренном треугольнике (длины боковых сторон равны) высота, проведенная к основанию, является медианой и биссектрисой. Углы при основании равнобедренного треугольника равны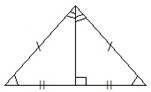
2. Сумма внутренних углов любого треугольника составляет 180°, т.е. ∠1+∠2+∠3=180°. Внешний угол треугольника (∠4) равен сумме двух внутренних, не смежных с ним, т.е. ∠4=∠1+∠2
3. Средняя линия треугольникасоединяет середины боковых сторон треугольника. Средняя линия треугольника параллельна основанию и равна его половине: MN=AC/2
4. Площадь треугольника:	Площадь треугольника через радиусы вписанной и описанной окружностей:
5. Формула Герона.
6. Центр тяжести треугольника -точка пересечения медиан, которая делит каждую медиану в отношении 2:1, считая от вершины. Длина медианы, проведенной к стороне а: .   Медиана делит треугольник на два равновеликих (равных по площади) треугольника, площадь каждого из этих двух треугольников равна половине площади данного треугольника.
7. Биссектриса угла любого треугольника делит противоположную сторону на части, соответственно пропорциональные боковым сторонам треугольника:
8. Центр окружности, вписанной в треугольник, лежит на пересечении биссектрис углов треугольника. Площадь треугольника SΔ=(½) P∙r, где P=a+b+c, r-радиус вписанной окружности. Радиус вписанной окружности можно найти по формуле:
9. Центр окружности, описанной около треугольника, лежит на пересечении серединных перпендикуляров к сторонам треугольника. Радиус окружности, описанной около любого треугольника:

1. Признаки равенства треугольников:

2. Признаки подобия треугольников:

3. Если острый угол одного прямоугольного треугольника равен острому углу другого прямоугольного треугольника, то такие треугольники подобны (следствие из первого признака подобия).
4. Отношение площадей двух подобных треугольников равно квадрату коэффициента подобия. (Коэффициент подобия равен отношению сходственных сторон).
5. Подобие треугольников – «треугольник в треугольнике»: Если ВС ǁ DE, то ΔАВС ~ ΔADE	6. Подобие треугольников – «бабочка»: Если АВ ǁ DE, то ΔАВС ~ ΔDEС
7. Если угол одного треугольника равен углу другого треугольника, то площади этих треугольников относятся как произведения сторон, заключающих равные углы.

Формулы для радиусов вписанных и описанных окружностей правильных многоугольников:

	Окружность, описанная около правильного n-угольника.
	Окружность, вписанная в правильный n-угольник.
Сумма внутренних углов любого выпуклого n-угольника равна 180°(n-2). Сумма внешних углов любого выпуклого n-угольника равна 360°.