Тема: Типы СМО
1. Классификация СМО
2. СМО с отказами. Уравнения Эрланга
3. Установившийся режим работы. Формулы Эрланга.
4. СМО с ожиданием
5. Системы смешанного типа с ограничениями по длине очереди
Классификация СМО
СМО делятся на два основных типа:
а) системы с отказами,
б) системы с ожиданием.
В системах с отказами заявка, поступившая в момент, когда все каналы обслуживания заняты, мгновенно получает отказ, покидает систему и в дальнейшем процессе обслуживания не принимает участие.
В системах с ожиданием заявка, поступившая в момент, когда все каналы обслуживания заняты, не покидает систему, а становится в очередь и ожидает, пока не станет свободным какой-либо канал.
Классификация СМО по видам потерь:
| СМО |
| без потерь |
| с потерями |
| с явными потерями |
| с условными потерями |
| с комбинированными потерями |
| с ожиданием |
| с повторением |
| с ограничениями |
| по длине очереди |
| по времени ожидания |
| по числу источников повторных вызовов |
Классификация СМО по наличию приоритета:
| СМО |
| без приоритета |
| с приоритетом |
| относительный приоритет |
| абсолютный приоритет |
| без дообслуживания |
| с дообслуживанием |
СМО с отказами. Уравнения Эрланга
Рассмотрим 
– канальную СМО с отказами как физическую систему 
с конечным числом состояний:
– свободны все каналы, хn
– занят точно один канал,
….
– занято точно 
каналов,
….
– занято все каналов.
Схема возможных переходов дана на рис.1.
| х0 |
| хk |
| хn |
| … |
| … |
Рис.1
Поставим задачу: определить вероятности состояния системы 
, 
, для любого момента времени 
. Задачу будем решать при таких допущениях:
1) поток заявок – пуассоновский, с плотностью потока заявок 
:
(1.1)
2) время обслуживания 
– экспоненциальный с параметром 
:
, (1.2)
Величину 
можно понимать как «плотность потока освобождений» занятого канала.
Поскольку оба потока – заявок и освобождения – простейшие, то процесс, протекающий в системе, будет марковским.
Рассмотрим возможные состояния системы МО и их вероятности
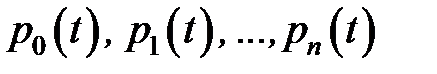(1.3)
Очевидно, для любого момента времени
(1.4) 
Запишем систему дифференциальных уравнений для вероятностей (1.3):
(1.5)
Уравнения (1.5) называются уравнениями Эрланга. Интегрирование системы уравнений (1.5) при начальных условиях 
, 
(в начальный момент все каналы свободны) даёт зависимость 
для любого 
. Вероятности характеризуют среднюю загруженность системы, и её изменение с течением времени. В случае, когда - вероятность того, что заявка, которая пришла в момент 
, застанет все каналы занятыми (получает отказ):
Величина 
называется относительной пропускной способностью системы. Для данного момента 
– отношение среднего числа заявок, которые обслужены в единицу времени, к среднему числу поданных заявок.
Система дифференциальных уравнений (1.5) относительно легко может быть проинтегрирована при любом конкретном числе каналов 
.
Уравнения (1.5) остаются справедливыми для 
и 
при условии, что потоки событий, которые переводят систему из состояния в состояние оставались пуассоновскими (без этого процесс не будет марковским).
Установившийся режим работы. Формулы Эрланга.
Рассмотрим – канальную СМО с отказами, на вход которой поступает пуассоновский поток заявок с плотностью 
; время обслуживания – по экспоненциальному закону с параметром . Возникает вопрос: будет ли стационарным случайный процесс, происходящий в системе? Очевидно, что сразу после включения системы в работу процесс, протекающий в ней ещё не будет стационарным: в системе МО (как в любой динамической системе) возникает так называемый «переходной», нестационарный процесс. Однако, через некоторое время, этот переходной процесс затухает, и система переходит на стационарный, так называемый режим, который «установился», вероятностные характеристики которого уже не будут зависеть от времени.
Во многих задачах практики интересуют именно характеристики граничного режима, который установился.
Можно доказать, что для любой системы с отказами такой граничный режим существует, т.е. при 
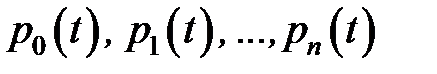все вероятности стремятся к постоянным пределам 
, а все их производные – к нулю.
Чтобы найти граничные вероятности (вероятности состояния системы в режиме, который установился), заменим в уравнениях Эрланга (1.5) все вероятности 
, 
, их пределами 
, а все производные полагаем равными нулю. Получим систему уже не дифференциальных, а алгебраических уравнений:
(2.1)
(2.2)
Введем обозначение
(2.3)
Величина 
называется приведенной плотностью потока заявок. Приведенная плотность потока заявокхарактеризует среднее число заявок, приходящихся на среднее время обслуживания заявки.
Из системы уравнений (2.1), и (2.2) находим:
(2.4)
Формула (2.4) выражает все вероятности 
через 
. Для того, чтобы выразить их непосредственно через и 
, нужно воспользоваться условием нормировки (2.2)
(2.5)
, , (2.6)
Формулы (2.6) называются формулами Эрланга. Они дают граничный закон распределения числа занятых каналов в зависимости от характера потока заявок и продуктивности СМО. Полагая в (2.6) 
, получим вероятность отказа (вероятность того, что заявка, которая поступила, застанет все каналы занятыми):
(2.7)
В частности, для 1-канальной системы (
)
, (2.8)
а относительная пропускная способность
(2.9)
Формулы Эрланга (2.6) и их следствия (2.8), (2.9) получены для случая экспоненциального распределения времени обслуживания. Доказано, что эти формулы имеют место и при любом законе распределения времени лишь при условии, чтобы входной поток был простейшим.
Пример 1. АТС имеет 4 линии связи. На станцию поступает простейший поток заявок с плотностью 
(три вызова в минуту). Вызов, поступающий в момент, когда все линии заняты, получает отказ. Средняя продолжительность разговора 2 мин. Найти: а) вероятность отказа; б) среднюю долю времени, на протяжении которого телефонная станция, в общем, не загружена.
Решение. Имеем 
; 
, 
.
а) По формуле (2.8) получим
б) По формуле (2.5) получим
.
Несмотря на то, что формулы Эрланга дают точные значения только при условии простейшего потока заявок, ними в некотором приближении можно пользоваться и в том случае, когда поток заявок отличный от простейшего (например, является стационарным потоком с ограниченным последействием). Формулами Эрланга можно приближенно пользоваться и в случае, когда система МО допускает ожидание заявки в очереди, но при этом срок ожидания мал в сравнении со средним временем обслуживания одной заявки.
Пример 2. Станция наведения истребителей имеет три канала. Каждый канал может одновременно наводить один истребитель на одну цель. Среднее время наведения истребителя на цель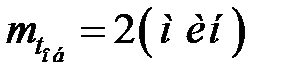 
. Поток целей простейший, с плотностью 
(самолетов в мин.). Станцию можно считать «системой с отказом», так как цель, на которую наведение не началось в момент, когда она вошла в зону действия истребителей, остается не атакованной. Найти среднюю долю целей, которые проходят через зону действия не обстрелянными.
Решение. 
, 
, 
.
.
Вероятность отказа 
выражает среднюю долю необстрелянных целей.
СМО с ожиданием
СМО называется системой с ожиданием, если заявка, которая застала все каналы занятыми, становится в очередь и ожидает, пока не освободится какой-либо канал.
Если время ожидания заявки в очереди ничем не ограничено, тогда система называется «чистой системой с ожиданием». Если время ограничено условиями, то система называется «системой смешанного типа». Это промежуточный случай между чистой системой с отказами и чистой системой с ожиданием.
Для практики наибольший интерес представляют системы смешанного типа.
Ограничения, которые накладываются на ожидание, могут быть разного типа. Часто бывает, что ограничение накладывается на время ожидания заявки в очереди; считается, что оно ограничено сверху каким-либо сроком 
, который может быть как строго определенным, так и случайным. При этом ограничивается только срок ожидания в очереди, а обслуживание, которое уже началось, доводится до конца, независимо от того, сколько времени продолжалось ожидание. В других задачах естественно накладывать ограничение не на время ожидания, а на время нахождения в системе или на число заявок в очереди.
В системах с ожиданием существенную роль играет так называемая «дисциплина очереди». Дисциплины постановки требований в очередь и выбора требования из неё для обслуживания определяют порядок, по которому требования становятся в очередь, если устройство для обслуживания занято, и порядок их выхода из очереди для обслуживания – если устройство для обслуживания свободно.
Простейшая дисциплина обслуживания предусматривает постановку требований в очередь по порядку их поступления. Она имеет название первый пришел – первым обслужили (ПППО) (FIFO – First In First Out). Примером очереди с такой дисциплиной может быть очередь к банкомату.
Существует также иной способ организации очереди, когда для обслуживания выбираются последние в очереди требования (последний пришел - первым обслужили (ПППО) (LIFO – Last In Fist Out). Этот способ называется стеком или магазином. Примером очереди с такой дисциплиной может быть паром, на котором перевозят авто. Автомобиль, который заехал первым, выезжает с парома последним.
Что касается правил выбора требований из очереди, то выбор может быть случайным (RANDOM). Во время выбора требований из очереди может учитываться их приоритетность.
Очередь может ограничиваться длиной или временем пребывания требования в очереди. Буферы данных широко используются в компьютерной технике. Во время обмена информацией между устройствами, которые имеют разную скорость обработки данных, информация накапливается в буфере, а потом используется устройством, имеющим меньшую скорость. Такие буферы организуются в системах введения – выведения данных в мультиплексорах. В компьютерных сетях буферы создают для организации очередей сообщений или пакетов.
Рассмотрим простейшую модель смешанной системы, которая является обобщением задачи Эрланга для системы с отказами. Для этого случая получим дифференциальные уравнения, аналогичные уравнениям Эрланга, и формулы для вероятностей состояний режима, который установился, аналогичные формулам Эрланга.
Рассмотрим смешанную СМО 
с 
каналами при таких условиях. На вход системы поступает простейший поток заявок с плотностью 
. Время обслуживания одной заявки 
распределено по экспоненциальному закону с параметром 
. Заявка, заставшая все каналы занятыми, становится в очередь и ожидает обслуживания; время ожидания ограничено некоторым сроком 
, если на протяжении этого срока заявка не будет принята к обслуживанию, то она покидает очередь и остается не обслуженной. Срок ожидания будем считать случайным и распределенным по экспоненциальному закону
где параметр 
– величина, обратная среднему времени ожидания:
, 
.
Параметр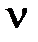 
полностью аналогичный параметрам 
и 
потока заявок и «потока освобождений». Его можно интерпретировать, как плотность «потока выходов» заявки, которая находится в очереди.
Очевидно, при 
система смешанного типа превращается в чистую систему с отказами; при 
она превращается в чистую систему с ожиданием.
Благодаря допущению о пуассоновском характере всех потоков событий, приводящих к изменению состояния системы, процесс, который протекает в ней, будет марковским. Запишем уравнения для вероятностей состояний системы. Состояния системы будем нумеровать не по числу занятых каналов, а по числу связанных с системой заявок. Заявку будем называть связанной с системой, если она или находится в состоянии обслуживания, или ожидает очереди. Возможными состояниями системы будут:
– ни один канал не занятый (очереди нет),
занятый точно один канал (очереди нет),
…………………………………………………….
заняты точно 
каналов (очереди нет),
…………………………………………………….
заняты все 
каналов (очереди нет),
заняты все 
каналов, одна заявка находится в очереди,
заняты все каналов, 
заявок находится в очереди,
………………………………………………………..
Число заявок 
, находящихся в очереди, в наших условиях может быть сколь угодно большим. Таким образом, система имеет бесконечное множество состояний.
Очевидно, первые 
дифференциальных уравнений ничем не будут отличаться от соответствующих уравнений Эрланга. Отличие новых уравнений от уравнений Эрланга начинается при 
. Действительно, в состояние 
система с отказами может перейти только из состояния 
, что касается системы с ожиданием, то она может перейти в состояние не только из , но и из состояния 
(все каналы заняты, одна заявка стоит в очереди).
Таким образом, ми получили для вероятностей состояний систему бесконечного числа дифференциальных уравнений:
(3.1)
Уравнения (3.1) являются обобщением уравнений Эрланга на случай системы смешанного типа с ограниченным временем ожидания. Параметры 
в этих уравнениях могут быть как постоянными, так и переменными. При интегрировании системы (3.1) нужно учитывать, что хотя теоретически число возможных состояний системы бесконечно, но на практике вероятности 
при увеличении 
становятся очень малыми, и соответствующие уравнения могут быть отброшены.
Получим формулы, аналогичные формулам Эрланга, для вероятностей состояний системы при режиме обслуживания, который установился (
). Из уравнений (3.1), полагая все 
, 
, постоянными, а все производные – равными нулю, получим систему алгебраических уравнений:
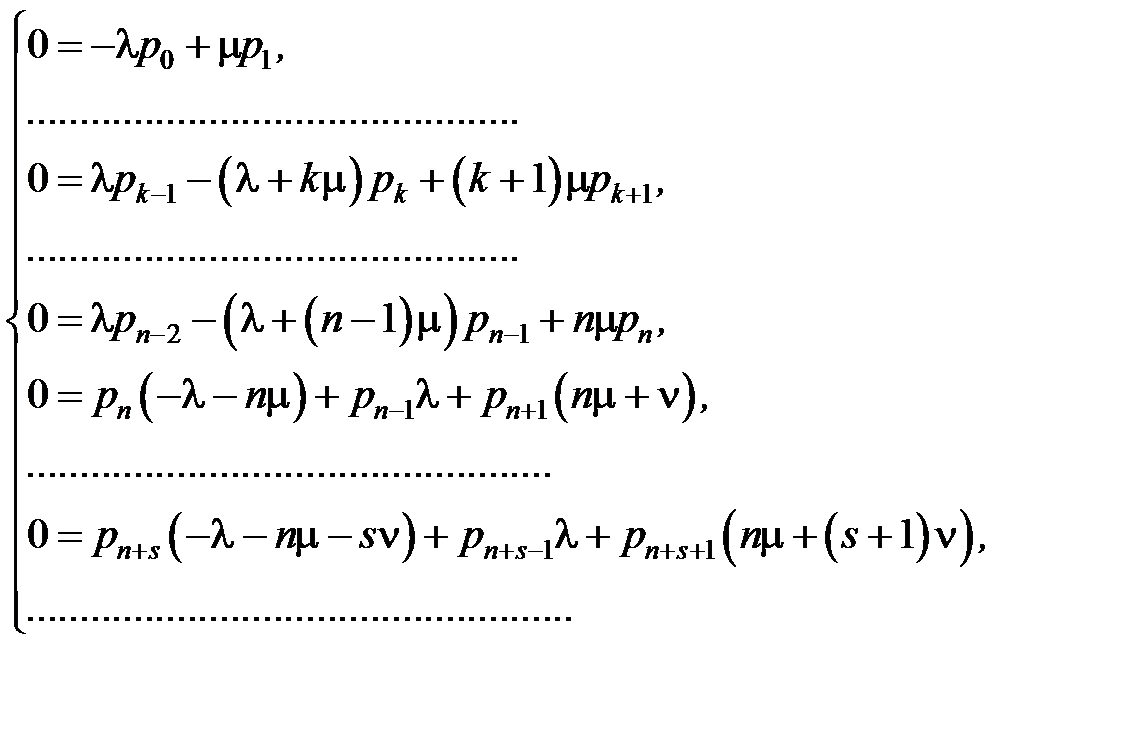
(3.2)
К ним нужно добавить условие нормировки:
(3.3)
Найдем решение системы (3.2), рассмотрев вместо плотностей 
и 
«приведенные» плотности:
(3.4)
Параметры 
выражают соответственно среднее число заявок и среднее число выходов заявки, находящейся в очереди, которые приходятся на среднее время обслуживания одной заявки.
, 
, (3.5)
(3.6)
Зная вероятности всех состояний системы, можно достаточно легко определить другие характеристики системы, а именно, вероятность 
того, что заявка покидает систему не обслуженной. Определим её из следующих соображений: при режиме, который установился, вероятность того, что заявка покидает систему не обслуженной, представляет собой отношение среднего числа заявок, выходящих из очереди в единицу времени, к среднему числу заявок, поступивших в единицу времени. Найдем среднее число заявок, выходящих из очереди в единицу времени. Для этого сначала вычислим математическое ожидание 
числа заявок, которые находятся в очереди:
(3.7)
Чтобы получить нужно, 
умножить на среднюю «плотность выходов» одной заявки 
и разделить на среднюю плотность заявок 
, т.е. умножить на коэффициент
Получим:
(3.8)
Относительная пропускная способность системы характеризуется вероятностью того, что заявка, поступившая в систему, будет обслужена:
.
Очевидно, что пропускная способность системы с ожиданием, при одних и тех же 
и 
будет всегда выше, чем пропускная способность системы с отказами: в случае наличия ожидания выходят не все заявки, которые застали каналы занятыми, а только некоторые. Пропускная способность увеличивается при увеличении среднего времени ожидания 
.
Очевидно, что при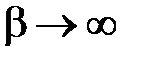 
система с ожиданием превращается в систему с отказами.
Рассмотрим другой граничный случай: чистую систему с ожиданием (
). В такой системе заявка вообще не выходит из очереди, и поэтому 
: заявка рано или поздно дождется обслуживания. Зато в чистой системе с ожиданием не всегда имеет место граничный стационарный режим при 
. Можно доказать, что такой режим существует лишь при 
, т.е. когда среднее число заявок, приходящихся на время обслуживания одной заявки, не выходит за границы возможностей – канальной системы. Если же 
, число заявок, находящихся в очереди, будет с течением времени неограниченно возрастать.
Допустим, что 
и найдем граничные вероятности 
, 
, для чистой системы с ожиданием.
(3.9)
(3.10)
Аналогично для 
(3.11)
Среднее число заявок, находящихся в очереди, определяется по формуле
(3.12)
Пример 3. На вход 3-канальной системы с неограниченным временем ожидания поступает простейший поток заявок с плотностью 
(заявки за час). Среднее время обслуживания одной заявки 
. Определить, существует ли установившийся режим обслуживания; если существует, то найти: вероятности 
, вероятность наличия очереди и среднюю длину очереди 
.
Решение. Имеем 
, 
. Поскольку 
, существует установившийся режим работы. Вычислим 
; 
.
Вероятность наличия очереди:
Средняя длина очереди равна 
(заявок).