1. Вычисление площадей плоских фигур.
Если 
- уравнение линии, ограничивающей криволинейную трапецию, то площадь трапеции S (в предположении, что 
) равна:
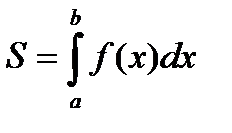, где a и b – абсциссы начала и конца линии.
В более общем случае, если площадь ограничена двумя кривыми 
и 
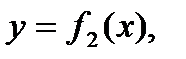где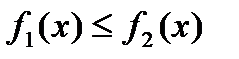 
и прямыми 
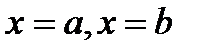при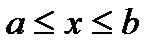 
, будем иметь
.
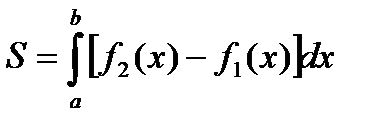Пример:
Вычислить площадь фигуры, ограниченной линиями 
Решение:
Находим точки пересечения параболы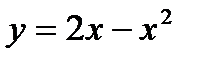 
и прямой 
.
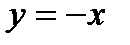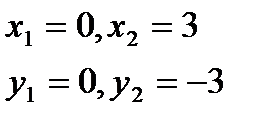
Построим область, ограниченную этими линиями.
;
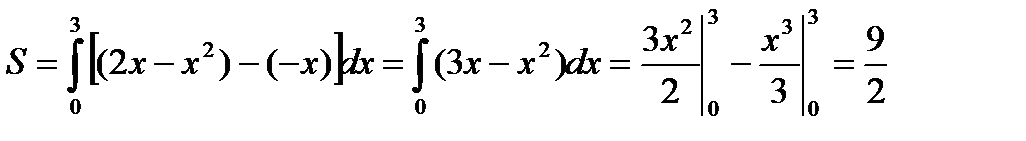Пример. Найти площадь фигуры, ограниченной линиями y = x, y = x2, x = 2.
Искомая площадь (заштрихована на рисунке) может быть найдена по формуле:
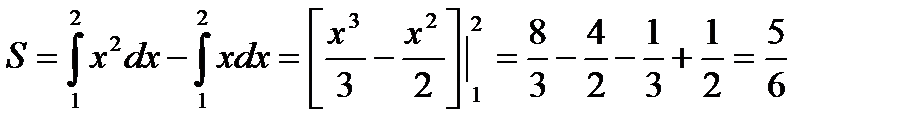(ед2)
2. Нахождение площади криволинейного сектора.
r = f(j)
b
О a r
Для нахождения площади криволинейного сектора введем полярную систему координат. Уравнение кривой, ограничивающей сектор в этой системе координат, имеет вид r = f(j), где r - длина радиус – вектора, соединяющего полюс с произвольной точкой кривой, а j - угол наклона этого радиус – вектора к полярной оси.
Площадь криволинейного сектора может быть найдена по формуле
3. Вычисление длины дуги кривой.
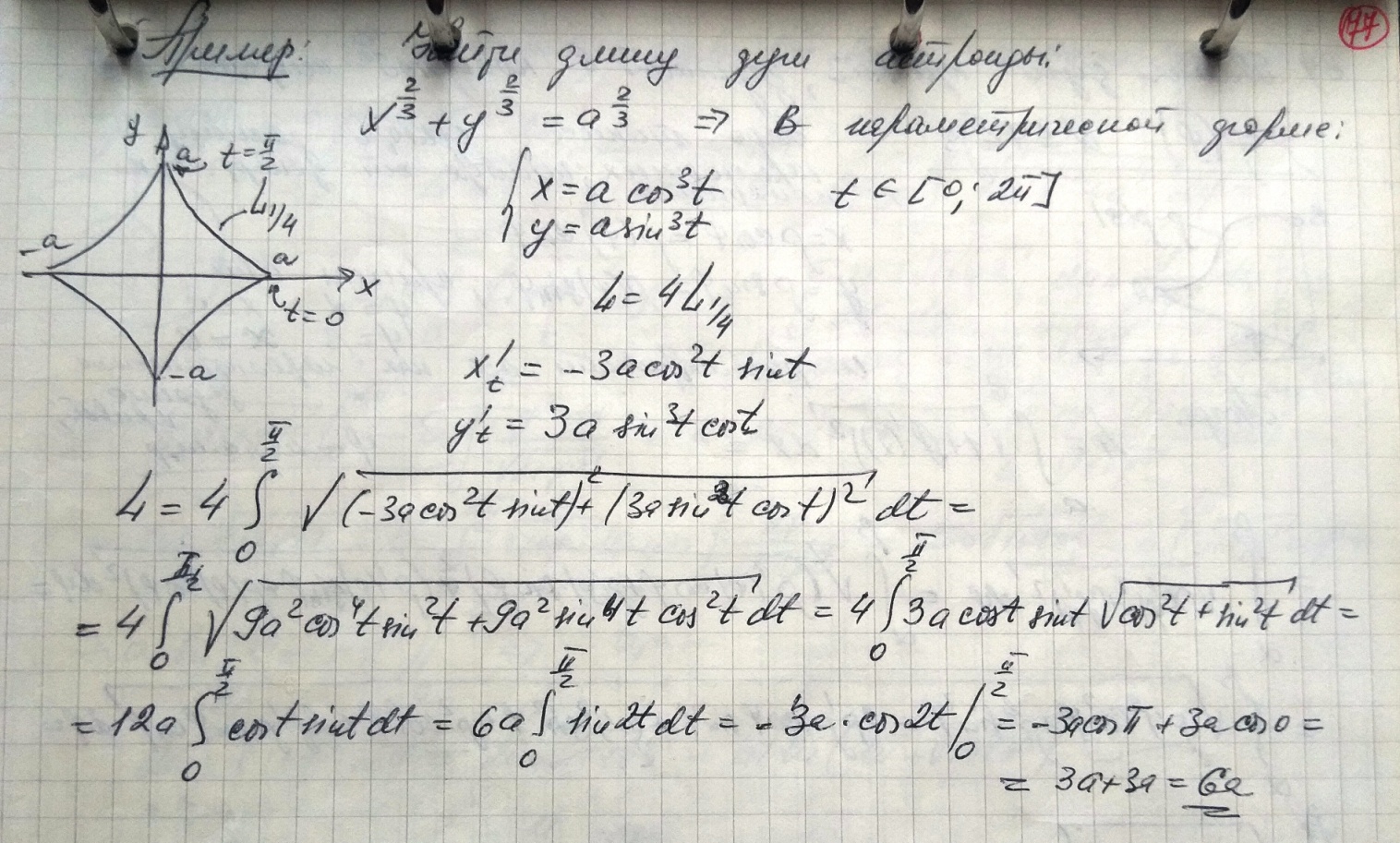
Пример: Найти длину окружности, заданной уравнением x2 + y2 = r2.
1 способ. Выразим из уравнения переменную у. 
Найдем производную 
Тогда 
Тогда S = 2pr. Получили общеизвестную формулу длины окружности.
2 способ. Если представить заданное уравнение в полярной системе координат, то получим: r2cos2j + r2sin2j = r2, т.е. функция r = f(j) = r, 
тогда
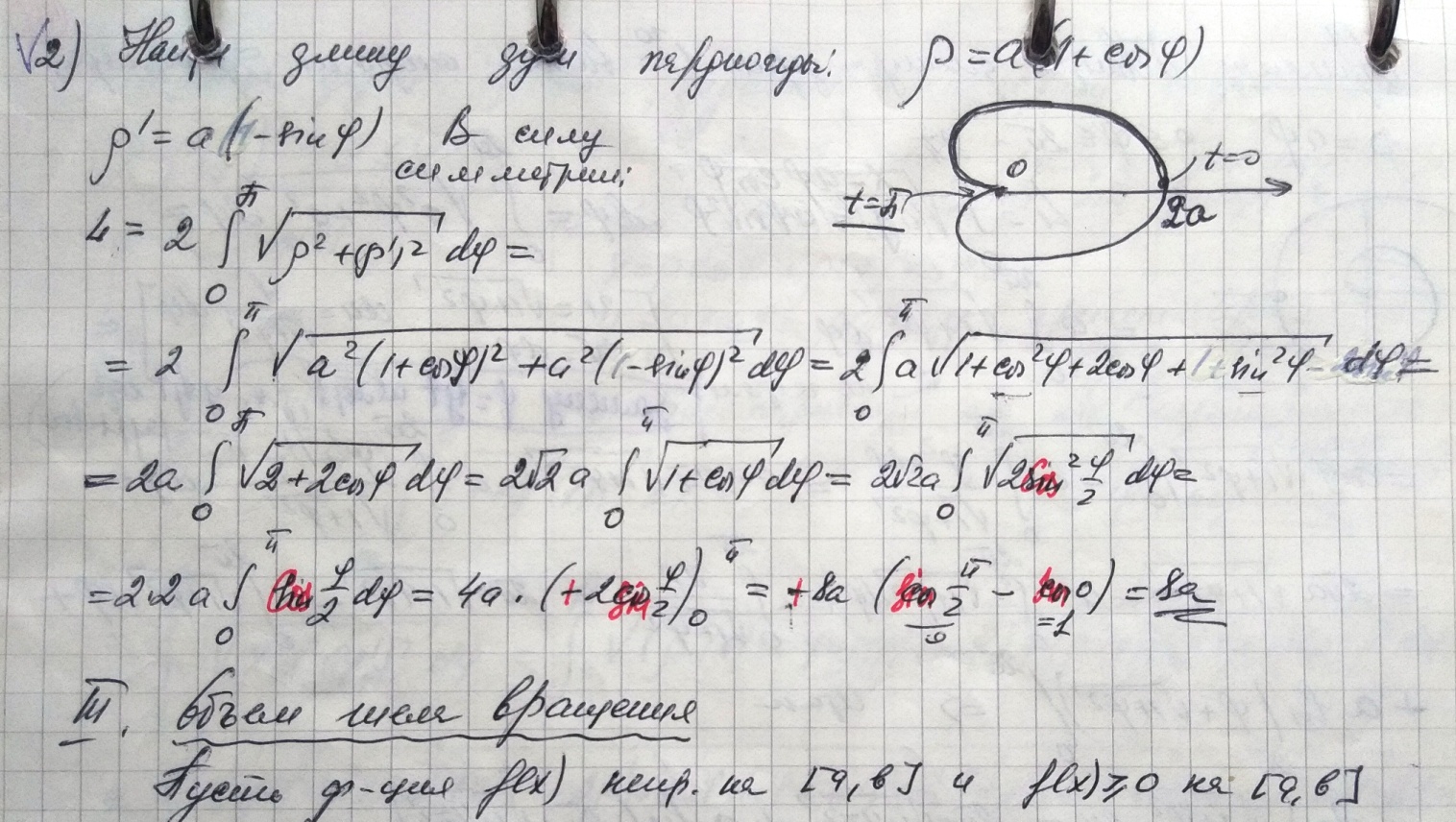
4. Вычисление объемов тел.
Вычисление объема тела по известным площадям его параллельных сечений.
Q(xi-1)
Q(xi)
a xi-1 xi b x
Пусть имеется тело объема V. Площадь любого поперечного сечения тела Q, известна как непрерывная функция Q = Q(x). Разобьем тело на “слои” поперечными сечениями, проходящими через точки хi разбиения отрезка [a, b]. Т.к. на каком- либо промежуточном отрезке разбиения [xi-1, xi] функция Q(x) непрерывна, то принимает на нем наибольшее и наименьшее значения. Обозначим их соответственно Mi и mi.
Если на этих наибольшем и наименьшем сечениях построить цилиндры с образующими, параллельными оси х, то объемы этих цилиндров будут соответственно равны MiDxi и miDxi здесь Dxi = xi - xi-1.
Произведя такие построения для всех отрезков разбиения, получим цилиндры, объемы которых равны соответственно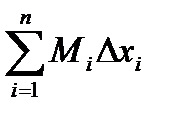 
и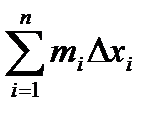 
.
При стремлении к нулю шага разбиения l, эти суммы имеют общий предел:
Таким образом, объем тела может быть найден по формуле:
Недостатком этой формулы является то, что для нахождения объема необходимо знать функцию Q(x), что весьма проблематично для сложных тел.
Пример: Найти объем шара радиуса R.
y
R y
-R 0 x R x
В поперечных сечениях шара получаются окружности переменного радиуса у. В зависимости от текущей координаты х этот радиус выражается по формуле 
.
Тогда функция площадей сечений имеет вид: Q(x) = 
.
Получаем объем шара:
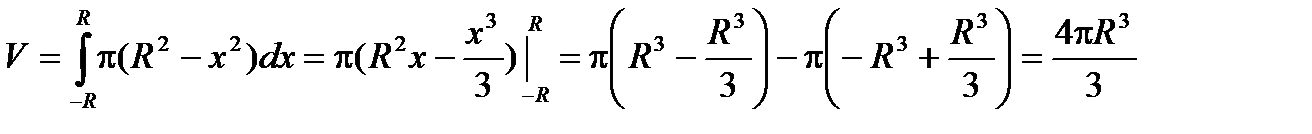
Пример: Найти объем произвольной пирамиды с высотой Н и площадью основания S.
Q S
x H x
При пересечении пирамиды плоскостями, перпендикулярными высоте, в сечении получаем фигуры, подобные основанию. Коэффициент подобия этих фигур равен отношению x/H, где х – расстояние от плоскости сечения до вершины пирамиды.
Из геометрии известно, что отношение площадей подобных фигур равно коэффициенту подобия в квадрате, т.е. 
Отсюда получаем функцию площадей сечений: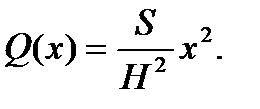 
Находим объем пирамиды: 
5. Объем тел вращения.
Рассмотрим кривую, заданную уравнением y = f(x). Предположим, что функция f(x) непрерывна на отрезке [a, b]. Если соответствующую ей криволинейную трапецию с основаниями а и b вращать вокруг оси Ох, то получим так называемое тело вращения.
y = f(x)
x
Т.к. каждое сечение тела плоскостью x = const представляет собой круг радиуса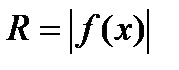 
, то объем тела вращения может быть легко найден по полученной выше формуле:
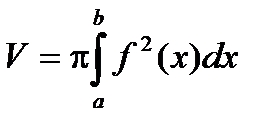
Если криволинейная трапеция, ограниченная линиями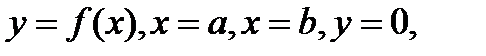 
вращается вокруг оси Ох, то объём полученного тела вращения
Если криволинейная трапеция, ограниченная линиями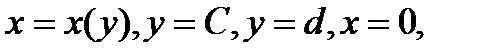 
вращается вокруг оси Оу, то объём полученного тела вращения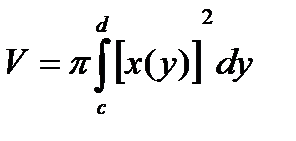 
Пример 1:
Найти объём тела, образованного вращением фигуры, ограниченной линиями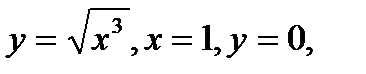 
вокруг оси Ох.
Решение:
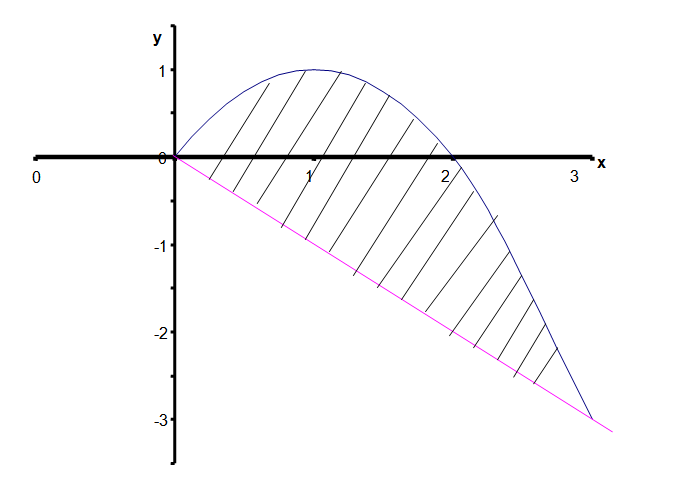
На рисунке указана штриховкой плоская область, которая вращается вокруг оси Ох.
Объём вычисляется по формуле 
.
Пример 2:
Найти объём тела, образованного вращением фигуры, ограниченной линиями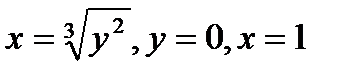 
, вокруг оси Оу.
Решение:
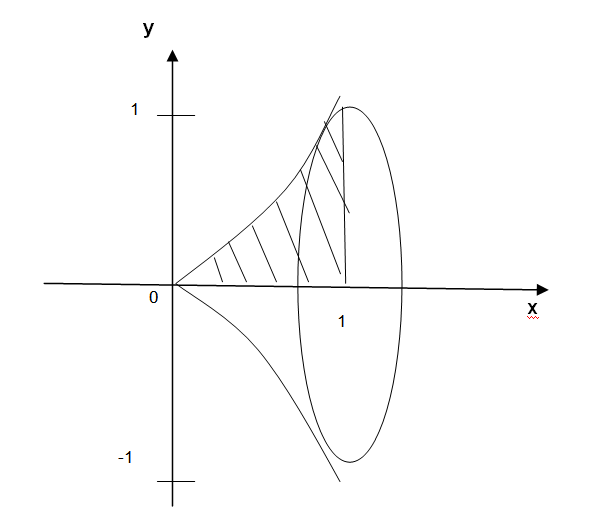
На рисунке указана штриховкой плоская область, которая вращается вокруг оси Оу.
| Х |
| У |
Объём вычисляется как разность объёма цилиндра и объёма тела, прилегающего к оси Оу.
Тогда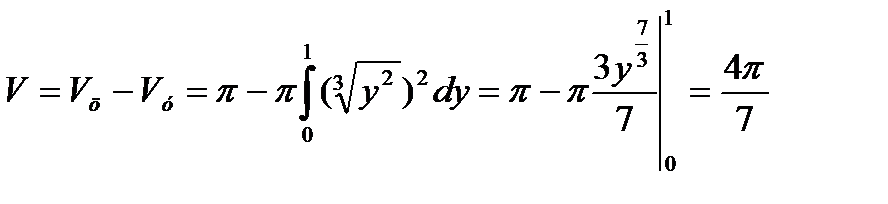 
.
6. Площадь поверхности тела вращения.
Мi B
А
х
xi
Определение: Площадью поверхности вращения кривой АВ вокруг данной оси называют предел, к которому стремятся площади поверхностей вращения ломаных, вписанных в кривую АВ, при стремлении к нулю наибольших из длин звеньев этих ломаных.
Тогда формула для вычисления площади поверхности тела вращения. 
