Вопросы, выносимые на экзамен, для студентов первого курса
(первый семестр)
Учебный год
- Определение матрицы. Виды матриц. Действия над матрицами.
- *Теорема об обратной матрице.
- Определители второго и третьего порядка. Свойства определителей, правила их вычисления.
- *Формулы Крамера.
- Прямоугольная и полярная система координат.
- Векторы и действия над ними.
- *Скалярное произведение векторов. Выражение скалярного произведения через координаты векторов.
- *Векторное произведение векторов. Выражение векторного произведения через координаты векторов.
- *Смешанное произведение векторов. Выражение смешанного произведения через координаты векторов.
- *Коллинеарные векторы. Условие коллинеарности векторов.
- *Ортогональные векторы. Условие ортогональности векторов.
- Компланарные векторы. Условие компланарности векторов.
- Приложения скалярного, векторного и смешанного произведений.
- * Виды уравнения прямой на плоскости и основные задачи на прямую.
- * Кривые второго порядка: окружность, эллипс, гипербола и парабола.
- *Уравнения прямой и плоскости в пространстве. Задачи на прямую и плоскость.
- Функция, способы задания, основные характеристики, обратная и сложная функция.
- Предел функции (в точке и при
 ), их геометрический смысл.
), их геометрический смысл. - * БМФ, теоремы о них и следствия из теорем.
- ББФ (в точке и при
 ), свойства ббф, связь между ббф и бмф.
), свойства ббф, связь между ббф и бмф. - *Теорема о связи между функцией, ее пределом и бмф.
- *Основные теоремы о пределах.
- *Признак существования предела функции.
- *Первый и второй замечательные пределы.
- *Сравнение бмф, таблица эквивалентных бмф при
 , теоремы о бмф.
, теоремы о бмф. - Непрерывные функции: определения, свойства, точки разрыва.
- *Определение производной, геометрический и механический смысл, основные теоремы о производных.
- Логарифмическое дифференцирование. Дифференцирование функций заданных параметрически и неявно.
- *Дифференциал функции, геометрический смысл, основные теоремы о дифференциалах.
- *Теорема Роля и Лагранжа.
- *Раскрытие неопределенностей. Виды неопределенностей. Теоремы Бернулл-Лопиталя для неопределенностей
 и
и  . Неопределенности вида
. Неопределенности вида  ;
;  ;
;  ;
;  .
. - Формула Тейлора.
- * Первый достаточный признак экстремума функции.
- * Монотонность функции. Необходимый и достаточный признак монотонности.
- * Экстремумы функции. Теорема Ферма.
- Выпуклость и вогнутость графика функции. Точки перегиба.
- * Асимптоты графика функции.
- *Первообразная. Терема о первообразной, о существовании неопределенного интеграла. Основные свойства неопределенного интеграла.
- Общие методы интегрирования для неопределенного интеграла: непосредственное, заменой переменной, по частям, интегрирование рациональных дробей, функций, рационально зависящих от тригонометрических, простейших алгебраических иррациональностей.
- * Определенный интеграл как предел интегральной суммы.
- * Формула Ньютона-Лейбница.
- Основные свойства определенного интеграла.
- *Геометрический смысл определенного интеграла.
- Методы интегрирования определенного интеграла.
- Несобственные интегралы.
- Приложения определенного интеграла: вычисление площади плоских фигур, длины дуги кривой, объемов тел, физический смысл.
- Комплексные числа, формы записи, действия над комплексными числами.
- Основные понятия функции нескольких переменных. Частные производные.
- Частные и полные дифференциалы. Условия дифференцируемости функций нескольких переменных.
- Производная сложной функции.
- Дифференцирование неявных функций.
- Касательная и нормаль к поверхности
- Достаточный признак существования экстремума дифференцируемой функции и правило нахождения.
ЛИНЕЙНАЯ АЛГЕБРА
- Найти
 , если
, если
а)  ,
,  .
.
б) 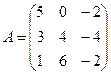 ,
,  .
.
2. Решить системы
а) 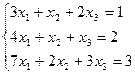 ; б)
; б)  .
.
в)  ; г)
; г)  .
.
ВЕКТОРНАЯ АЛГЕБРА
1. Даны векторы  ,
,  ,
,  .
.
Найти координаты вектора 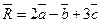 и его длину.
и его длину.
2. Векторы  и
и  образуют угол
образуют угол  . Найти
. Найти  , если
, если  ,
,  .
.
3.При каких  и
и  векторы
векторы  и
и  коллинеарны?
коллинеарны?
4. При каком  векторы
векторы  и
и  ортогональны?
ортогональны?
5. Компланарны ли векторы  ;
;  ;
;  ?
?
6. Даны векторы:  ,
,  . Найти:
. Найти:
1)  ; 2)
; 2)  ; 3)
; 3)  .
.
7. Дан треугольник с вершинами  ,
,  и
и  . Найти внутренний угол при вершине
. Найти внутренний угол при вершине  .
.
8. Даны вершины треугольника  ,
,  ,
,  . Вычислить его площадь.
. Вычислить его площадь.
8. В пирамиде  , где
, где  ,
,  ,
,  ,
,  найти
найти  .
.
9. Какую тройку образуют векторы  ,
,  ,
,  ?
?
ПРЕДЕЛ ФУНКЦИИ
1.  ;
2. ;
2.  ;
3. ;
3.  ;
4. ;
4.  ;
5. ;
5.  ;
6. ;
6.  ;
7. ;
7.  . .
|
8.  ;
9. ;
9.  ;
10. ;
10.  ;
11. ;
11.  ;
12. ;
12.  ;
13. ;
13.  ;
14. ;
14.  . .
|
ПРОИЗВОДНАЯ
Найти 
1. а)  б)
б) 
2. а)  б)
б) 
3. а)  б)
б) 
4. а)  б)
б) 
5. а)  б)
б) 
6. а)  б)
б) 
7. Найти 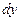
а)  б)
б) 
Применение производных.
1. Найти пределы функций, используя правило Лопиталя:
а)  б)
б)  в)
в) 
г)  д)
д)  е)
е)  .
.
2. Найти интервалы монотонности и экстремумы функции:
а)  б)
б)  в)
в)  .
.
3. Найти интервалы выпуклости и вогнутости, точки перегиба графика функции:
а)  б)
б)  в)
в)  ;
;
4. Найти вертикальные и наклонные асимптоты графика функции:
а)  б)
б)  в)
в)  ;
;
Комплексные числа.
1. Представить в тригонометрической и показательной формах комплексные числа:
а)  б)
б)  в)
в)  г)
г) 
| д)  е)
е) 
|
2. Выполнить действие:
а)  б)
б)  в)
в) 
| г)  д)
д) 
|
Неопределенный интеграл.
1. Непосредственное интегрирование:
 .
.



2. Интегрирование заменой переменной:
а)  ;
б) ;
б)  ;
в) ;
в)  ; ;
| г)  ;
д) ;
д)  . .
|
3. Интегрирование по частям:
а)  ;
б) ;
б)  ;
в) ;
в)  ; ;
| г)  ;
д) ;
д)  . .
|
4. Интегрирование дробно рациональных функций:
а)  ;
б) ;
б)  ; ;
| в)  ;
г ;
г  . .
|
5. Интегрирование функций, рационально зависящих от тригонометрических:
а)  ;
б) ;
б)  ;
в) ;
в)  ; ;
| г)  ;
д) ;
д) 
|
6. Интегрирование простейших алгебраических иррациональностей:
а)  ;
б) ;
б)  ; ;
| в)  ; ;
|
ОпределенныЙ интеграл
1. Вычислить:
а)  ;
б) ;
б)  ;
в) ;
в)  ; ;
| г)  ;
д) ;
д)  ;
е) ;
е)  . .
|
2. Исследовать сходимость несобственных интегралов (по определению):
а)  ;
г) ;
г)  ; ;
| б) 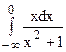 ;
д) ;
д)  ; ;
| в)  ;
е) ;
е)  . .
|
3. Вычислить площадь плоских фигур, ограниченных линиями:
а)  ;
;
б)  .
.
в) первой аркой циклоиды  и осью ОХ.
и осью ОХ.
г) астроидой 
д) кардиоидой  ;
;
ж) четырех лепестковой розой 
4. Найти длины дуг кривых:
а) параболы  , отсеченной осью ОХ;
, отсеченной осью ОХ;
в) астроиды  ; г)
; г) 
д) кардиоиды  ; ж) первого витка спирали Архимеда:
; ж) первого витка спирали Архимеда:  .
.
5. Вычислить объем тела, полученного вращением.
а) вокруг оси ОХ фигуры, ограниченной линиями 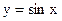 ,
,  , если
, если  ;
;
б) вокруг оси ОУ фигуры, ограниченной линиями  ,
,  ,
,  .
.
в) вокруг оси ОХ фигуры, ограниченной линиями  ,
,  .
.
Дифференциальное исчисление функций нескольких переменных.
Найтии построить область определения функции  .
.
Найтии построить область определения функции  .
.
Найти частную производную функции  по
по  .
.
Найти частную производную функции  по
по  .
.
Найти частную производную функции  по
по  .
.
Найти частную производную функции 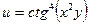 по
по  .
.
Найти частный дифференциал по  функции
функции  .
.
Найти частный дифференциал по  функции
функции  .
.
Найти полный дифференциал функции  .
.
Найти производную  функции
функции  , заданной неявно, если
, заданной неявно, если  .
.
Найти частную производную  функции
функции  по
по  , заданной неявно, если,
, заданной неявно, если,  .
.
Найти производную  сложной функции, если
сложной функции, если  , где
, где  .
.
Найти производную  сложной функции, если
сложной функции, если  , где
, где  .
.
Найти частную производную  сложной функции, если
сложной функции, если  , где
, где 
 .
.
Составить уравнение касательной плоскости и нормали к поверхности
 в т.
в т.  .
.