Рассмотрим функцию f(
)=)= 
-. Исследуем эту функцию на экстремум учитывая что | 
’|=1 (условие).
=1
Строим функцию F: F(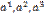
)= f(a1,a2,a3)-λ 
-1. Ищем безусловный экстремум функции F который является экстремумом для f’ 
=0, i=1,2,3
= 
+ 
= 
+ 
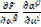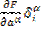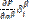приравниваем частные производные к 0: 
+ 
-λ 
-λ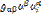 
=0
+ 
- λ 
-λ 
=0 
- λ = 
-λ 
) 
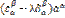=0
=0, 
=1,2,3 (3) –уравнение для определения параметров 
Т.к. в уравнении поиска параметра 
в рассматриваемой задаче на условный экстремум функции F совпадает в точности с уравнением в задаче по поиску главных направлений тензора деформации, то отсюда следует, что главные векторы тензора деформации нормированного единецей, экстримальные значения функции F принимает когда параметры 
являются единственными векторами главный направлений тензора деформации.
Пусть 
, k=1,2,3. | 
|=1, 
-главные век. Тензора деформации. Тогда выписывается следующее равенство 
| 
| 
= 
= 
= 
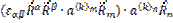, а это f(
)= 
Функция, при условии пап=1, принимает экстрим. Значения на главных направлениях тензора деформации. Эти экстримальные значения равны главным значениям тензора деформации.
Рассмотрим относительное уравнение 
–является ортом
Действительно: 
, 
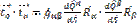=1
Условия совместности деформаций
Зададим:
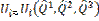– компоненты век перемещения
Найдем компоненты деформации
А если задать компоненты деф-ии, то найдутся такие перемещения, которые должны этим деформациям соответствовать.
Здесь задача переопределена: задаем 6 функций, а находим только 3, для того чтобы эту 
должны быть ограничения, которые называются условиями совместимости. Построим эти ограничения:
= 
) (**)
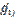
2 
- 
2 
(*)
; 
)
Подставляем (*) в (**)
= 
= 
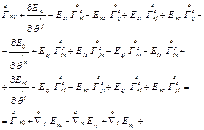
2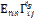 
= 
+ 
- 
=
- 
+ 
+ - 
|* 
= 
+ 
,
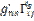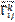где = (
- 
)
Вычислим производную
= 
- 
= 
- 
= 
+ 
- = 
=
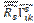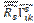– условие совместности
Различные виды малых деформаций
Р-м ф-ию для относит. Удлинений в направлении коорд. оси:
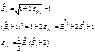
Пусть рассматр. задача, в которой относит. Удлинение малы:
тогда квадратами можно пренебречь => 
Рассмотрим ф-лу для сдвига:
Р-м случай, когда сдвиги малы: 
Если малы относит. удлинения и сдвиги:
Т.о. 
симметр, кососим.
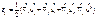
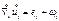
Кососиметр. Тензор с ik отвечает за поворот элемент. объема как в абсолютно тв. тела, т.е. элемент. Объем поступательно переходит в т-у, потом поворачив. Как абсолютно тв. тело, а потом происходят удлинения и сдвиги
Возмем гл. компоненты тензора eij Он симметричен. Имеет гл. напр-ия об-их через 
и примем в качестве ск в отч. конф
| Чтобы выяснить, как 3ка в-ов деформируется, вспомним:
|
Ск ортонорм => верхн. и нижн. индексы не разл =>
Возьмем мом. эл-т напр-й по 
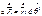
он перейдет в эл-т: 
учитывая 
| 
|
пусть кроме отност. удлинений и сдвигов 
малы и повороты 
т.к. малы, то того же пор-ка малости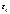 
=>
=> малы 
=> 
eij наз. тензором малых дифформаций
=> 
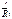отл. от 
на малую величину
т.е. можно не разл. отч. и тек. конф.
Геом. лин. случай деформирования СС
Принимается, что перемещения т.к. среды ui малы по сравнию с характерным лин. размером. тела V:
| L – характ. размер тела – min размер |
радиус в-р 
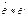=> исчезает разница между матер. и простр. коорд.