I I I Практические задания

Вопросы к экзамену по математическому анализу для 1 курс д/о,

специальность ²информатика² (бак). Декабрь, 2011 г.

Билет содержит три вопроса:
1) определения понятий, формулировки теорем,

2) вывод формул, доказательства теорем,

3) практические задания.

I Определения понятий, формулировки теорем

1. Аксиоматика множества действительных чисел.
2. Числовые функции. Определение, способы задания, свойства.
3. Степенная функция, ее свойства и график.
4. Обратимость функции. Показательная и логарифмическая функции.
5. Тригонометрические функции, их свойства и графики.
6. Обратные тригонометрические функции, их свойства и графики.
7. Последовательность (определение, способы задания, свойства).
8. Арифметическая и геометрическая прогрессии.
9. Бесконечно большие и бесконечно малые последовательности.
   Свойства бесконечно малых последовательностей.
10. Предел числовой последовательности.
11. Число .
12. Предел функции на бесконечности.
13. Арифметические операции над пределами функций.
14. Бесконечно малые и бесконечно большие функции. Их свойства.
15. Предел функции в точке. Односторонние пределы.
16. Асимптоты к графику функции.
17. Непрерывность функции в точке. Свойства непрерывных функций.
18. Непрерывность функции в точке. Классификация точек разрыва.
19. Производная функции в точке. Ее геометрический и физический смысл.
20. Дифференцируемость функции в точке. Дифференциал.
21. Правила дифференцирования.

I I Вывод формул, доказательства теорем

1. Теорема о пределе суммы двух последовательностей.
2. Связь между ограниченностью последовательности и наличием у нее предела.
3. Теорема Вейерштрасса о пределе монотонной последовательности.
4. Теорема о пределе промежуточной последовательности.
5. Сумма бесконечно убывающей геометрической прогрессии.
6. Сравнение бесконечно малых функций. Первый замечательный предел.
7. Сравнение бесконечно малых функций. Второй замечательный предел.
8. Задача о мгновенной скорости.
9. Задача об угловом коэффициенте касательной.
10. Уравнение касательной и нормали к графику функции.
11. Правила дифференцирования. Производная суммы и произведения.
12. Дифференцирование композиции функций.
13. Дифференцирование обратной функции.
14. Дифференцирование степенной функции.
15. Дифференцирование показательной функции.
16. Дифференцирование логарифмической функции.
17. Дифференцирование тригонометрических функций.
18. Дифференцирование обратных тригонометрических функций.

19. Необходимое условие точки экстремума (теорема Ферма).

20. Условие постоянства функции. Исследование функции на монотонность и экстремумы.

21. Понятие выпуклости функции. Исследование функции на выпуклость и точки перегиба.

I I I Практические задания

1. Постройте график функции и исследуйте на обратимость.
2. Найдите функцию, обратную для функции .
   Постройте графики этих взаимно-обратных функций и сравните их свойства.

1. Постройте график функции . С помощью элементарных преобразований получите из него график функции . Опишите свойства этой функции.

4 - 7. Вычислите предел последовательности:

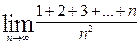
8 - 14. Вычислите предел функции:

	,

15 - 16. Найдите асимптоты к графику функции:

17. Найти уравнение касательной и нормали к графику функции в точке с абсциссой . Сделать графическую иллюстрацию к задаче.

18. Найти уравнение касательной и нормали к графику функции в точке с абсциссой . Сделать графическую иллюстрацию к задаче.

19 - 21. Применяя правила и формулы дифференцирования, найдите производную функции:
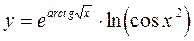