Массовые силы это силы тяжести и инерции.

Специальные жидкости.

 

Предмет гидравлики

Раздел механики, в котором изучают равновесие и движение жидкости, силовое взаимодействие жидкости с твердыми телами и газами, называют гидромеханикой.

Прикладная часть гидромеханики, которая характеризуется определен-ным кругом инженерных вопросов, задач и методов их решения, называется гидравликой.

Предметом гидравлики являются способы приложения законов равно-весия и движения жидкостей к решению инженерных задач.

Гидравлика дает методы расчета и проектирования гидротехнических сооружений (мостов, плотин, каналов, водосливов, водопроводов), а также гидромашин и гидроаппаратов (насосов, гидротурбин, гидропередач, гидро-распределителей, клапанов и т. п.).

В гидравлике, при анализе явлений, возникающих в жидкостях, находящихся в состоянии покоя или движения, используются как теоретические, так и экспериментальные методы исследований. Достаточно широко применяются упрощенные приемы решения некоторых задач. В гидравлике главную роль играет опыт, дающий основу для исследований.

В гидравлике рассматривают потоки жидкости, ограниченные и направленные твердыми стенками, т.е. течение в руслах и каналах.

Жидкость представляют однородной непрерывной средой без пустот и промежутков, а бесконечно малые частицы жидкости представляют большим числом молекул (не одной молекулой).

Термину «жидкость» в гидромеханике придают более широкий смысл, чем это принято на бытовом уровне.

В понятие «жидкость» включают вещества, обладающие свойством текучести – способность изменять форму при сколь угодно малых внешних силах. Значит газы тоже жидкости, но с меньшей плотностью.

Самая легкая жидкость – насыщенный раствор лития в жидком аммиаке (плотность 480 кг/м³). Плотность сжиженного водорода 78 кг/м³.

Самый тяжелый газ – гексафторид урана (плотность 15,2 кг/м³).

Воздух – 1,26 кг/м³.

Когда говорят о жидкости добавляют слово «капельные».

Капельные жидкости (вода, бензин, спирт, молоко, духи и др.) обладает следующими свойствами:

- большой подвижностью частиц (текучестью);

- сцеплением, или способностью сопротивляться силам разрыва;

- вязкостью – свойством сопротивляться сдвигающим усилиям;

- смачиванием, или способностью в определенных условиях «прили-пать» к твердым поверхностям;

- капиллярностью – способностью подниматься в смачиваемых ею трубках малого диаметра (за счет сил поверхностного натяжения).

- весьма малой сжимаемостью по сравнению с газами.

Гидравлика – инженерная наука, изучающая законы равновесия и движения в основном капельных жидкостей и методы их применения в инженерной практике. Она состоит из двух частей:

- гидростатики – где рассматриваются законы равновесия жидкостей;

- гидродинамики – где изучаются законы движения жидкостей.

Силы, действующие в жидких и газовых средах. Давление.

В гидравлике жидкость разделяют на реальную и идеальную. Идеальная жидкость – это упрощенная модель капельной жидкости: она не обладает внутренним и внешним трением и является несжимаемой. Это понятие введено для упрощения аналитических исследований.

Реальная жидкость обладает указанными свойствами.

 

Из-за текучести в жидкостях действуют не сосредоточенные силы, какие действуют на твердые тела, а распределенные по поверхности и объему силы, поэтому их разделяют на массовые (объемные) и поверхност-ные.

Массовые силы это силы тяжести и инерции.

Силы тяжести в земных условиях действует на жидкость постоянно, и в соответствии со вторым законом Ньютона, пропорциональны массе жидкос-ти.

Силы инерции, так же пропорциональные массе, действуют при относительном покое в ускоренно движущихся сосудах или при относительном движении жидкости в руслах, перемещающихся с ускорением.

 

Поверхностные силы действуют на границах раздела соседних объемов жидкости, газа или твердых тел. Они непрерывно распределены по поверхности и пропорциональны площади этой поверхности. В соответствии с третьим законом Ньютона, с такими же силами, но противоположно направленными, жидкость действует на соседние с нею объемы или тела.

В гидравлике оперируют относительными, единичными силами, отнесенными к единице массы (массовые силы) и к единице поверхности (поверхностные силы).

Единичная массовая сила (отнесенная к массе) численно равна соот-ветствующему ускорению:

Н/кг = [(кг ·м)/с²] / кг = м/с².

Единичная поверхностная сила (отнесенная к площади) измеряется в Н/м² (или кгс/см²), называется напряжением и имеет две составляющие – нормальную и касательную.

Касательная составляющая напряжения – это относительная сила трения между слоями жидкости или между жидкостью и твердой стенкой (Н/м²).

Нормальная составляющая напряжения – это давление (Н/м²).

 

В жидкостях, как и в газах, действуют и силы упругости, возникающие как реакция на внешнее давление.

 

Архимедова сила, проявляется во взаимодействии капельных жидкос-тей и газов с твердыми телами, погруженными в жидкую или газовую среду. Она вытесняет телотуда, где плотность среды минимальна.

Согласно закону Архимеда эта сила численно равна весу жидкости (газа), вытесненной телом, и приложена к центру тяжести вытесненного объема.

За единицу давления в Международной системе единиц (система СИ) принят Паскаль – давление, вызываемое силой 1 Н, равномерно распределенной по поверхности, площадью 1 м²: 1 Па = Н/м².

В случае покоя жидкости оно называется гидростатическим; в случае движения – гидродинамическим или просто давлением.

Если давление Р отсчитывают от абсолютного нуля, то его называют аб-солютным Р _абс, если от относительного нуля (атмосферного давления), то – избыточным Р _изб (или манометрическим).

Атмосферное давление над уровнем моря при температуре + 20 °C (или 293,15 °K) равно одной физической атмосфере:

Р_а = 1 атм = 760 мм. рт ст. = 101325 Па.

 

Рис. 1.1. Схем к определению давлений.

Указанные величины соответствуют так называемым нормальным условиям.

Кроме физической, используют техническую атмосферу:

Р = 1 атм = 1 кгс/см² = 98100 Па

Абсолютное и избыточное давление связаны между собой выражением:

Р _абс = Р_а + Р _изб

В инженерном деле применяют систему единиц МКГСС (техническая система единиц: метр, килограмм сила, секунда), в которой за единицу давления принимается одна техническая атмосфера (1 кгс/см²).

 

Силы, действующие в газах, так же можно разделить на поверхност­ные, пропорциональные величине поверхности, например, силы давления и силы вязкости, и объемные (массовые), про­порциональные объему или массе газа и действующие на каждую частицу газа, заключенного в данном объеме (например, сила тя­жести и силы инерции).

Поверхностные силы, отнесенные к еди­нице поверхности, так же называются напряжениями(касатель­ное и нормальное напряжения).

Движение газов в трубах может происходить под дейст­вием различных сил. В том случае, когда это движение происходит под действием сил тяжести, возникших из-за разности температур газа в различных местах трубопрово­да, движение носит название естественного.

Движение газов в ка­налах под действием внешних причин (из-за работы компрессора) называется принудительным.

1.3. Свойства капельных жидкостей и газов

Плотность и удельный вес жидкостей и газов.

Плотностью ρ капельной жидкости или газа называется масса жидкости или газа m, заключенная в единице объема V, кг/м³:

(1.1)

Удельный вес γ – это вес жидкости или газа G, отнесенный к занима-емому объему V, Н/м³:

(1.2)

Плотность пресной воды при 4 ºС равна 1000 кг/м³. Плотность газов измеряется в тех же единицах (кг/м³), но их плотность значительно меньше.

 

Так, воздух при нормальных условиях (Т = 20 °С и Р = 760 мм. рт. ст.) обладает плотностью примерно ρ _в ~ 1,26 кг/м³, следовательно воздух почти в восемьсот раз легче пресной воды.

 

Удельный вес жидкостей и газов связан с плотностью соотношением:

γ = ρg. (1.3)

Растворимость газов в жидкостях

Растворимость газов в жидкостях характеризуется количеством раство-ренного газа (в большинстве случаев – воздуха) в единице объема жидкости; она различна для разных жидкостей и изменяется с увеличением давления.

Относительный объем газа, растворенного в жидкости до ее полного насыщения, определяется по закону Генри:

(1.4)

где V_р – объем растворенного газа, приведенный к нормальным условиям (разд. 1.2.), V_ж – объем жидкости, k – коэффициент растворимости, р – давле-ние, под которым находится жидкость, р ₀ – давление, соответствующее нор-мальным условиям.

Коэффициент k является безразмерным и при температуре 20 °С имеет следующие значения: для пресной воды 0,016, для минеральных масел ~ 0,08, для наиболее распространенного гидравлического масла АМГ-10– 0,1.

При понижении давления, растворенный в жидкости газ выделяется, жидкость частично дегазируется.

Кроме растворенной газовоздушной составляющей, в жидкости всегда присутствует и нерастворенная составляющая в виде пузырьков, количество которых определяется силами поверхностного натяжения, давлением, мест-ными скоростями движения жидкости и периодом циркуляции жидкости в гидросистеме.

Из-за присутствия в жидкости растворенной (Р -фаза) и нерастворенной (Г -фаза) составляющих возникают трудности их удаления при заполнении рабочих пространств гидросистем.

Поэтому рабочая жидкость почти всегда является двухфазной средой. В работающем гидроприводе обе фазы непрерывно переходят одна в другую и их содержание нестабильно.

 

Содержание фаз оценивается параметрами α и λ отношениями:

растворенная:

нерастворенная

где V_Р – объем растворенной газовоздушной составляющей, V_Г – объем фазы Г, V_С – объем смеси жидкости и газа при нормальных условиях.

Количество нерастворенного газа зависит от вязкости. На рис. 2 показана зависимость параметра λ от вязкости рабочей жидкости.

 

Рис. 1.2. Зависимость содержания фазы Г от вязкости рабочей жидкости

Зависимость λ = f (ν) при ν > 40 сСт (4·10^-5 м²/с) является линейной и хорошо описывается эмпирической формулой:

В неподвижной жидкости происходит подъем пузырьков нерастворен-ного газа к свободной поверхности, при этом большая часть фазы Г выходит из жидкости с образованием пены, а меньшая часть переходит в фазу Р в соответствии с законом Генри.

Пузырьки размером менее 10 мкм находятся во взвешенном состоянии, на стенках и в микротрещинах и почти не всплывают, поэтому при прохож-дении жидкости через гидомашину при существенном повышении давления, пузырьки деформируются и нагреваются, что является одной из основных причин нагрева рабочей жидкости в работающем гидроприводе.

 

Так, если повышение температуры происходит за малый промежуток времени, в котором отвод тепла исчезающее мал, то температура после за-вершения сжатия может быть рассчитана по формуле:

(1.5)

где индексы 1 и 2 относятся к начальному и конечному состояниям соответственно, n – показатель адиабаты, зависящий от физических свойств фазы Г (1,39…1,78).

Повышение температуры в мелких пузырьках нерастворенной газовоздушной составляющей может достигать значений до 1000 °С и это приводит к эрозии поверхностей резиновых и полимерных уплотнений, соединительных рукавов и преждевременному их разрушению.

Сжимаемость жидкостей и газов

Сжимаемость – это способность жидкости деформироваться (изменять объем) под действием давления. Деформационная способность характеризуется коэффициентом объемного сжатия, равным относительному изменению объема, приходящемуся на единицу давления, м²/Н:

(1.6)

где V – первоначальный объем жидкости, dV – изменение этого объема, при увеличении давления на величину dP.

Знак минус обусловлен тем, что положительному приращению давления Р соответствует отрицательное приращение (т.е. уменьшение) объема.

Величина обратная β называется модулем объемной упругости жидкости, существенно зависящим от нерастворенной газовоздушной составляющей – фазы Г, Н/м²:

(1.7)

Для воды k = 2000 МПа, для минерального масла k = 1200 МПа.

Если жидкость сжимается, то изменяется и ее плотность, но в большинстве случаев (обычно при Р < 40 МПа) сжимаемостью и изменением плотности пренебрегают, так как они незначительны.

В тех случаях, когда учитывать изменение плотности жидкости при увеличении давления необходимо, пользуются формулой:

(1.8)

где ρ ₀ и Р ₀ – плотность и давление жидкости в нормальных условиях.

На рис. 1.3 показаны зависимости плотности воды и минеральных масел от давления.

 

Рис. 1.3. Зависимости

плотность – давление

 

 

 

 

Такие зависимости установлены для всех жидкостей и приводятся в справочной литературе. По ним плотность жидкости при заданном давлении можно просто считывать по соответствующим кривым.

У капельных жидкостей модуль упругости зависит от частоты ω ее деформации.

При медленном нагружении жидкости ω → 0 модуль объемной упругости k называется равновесным или изотермическим. При быстром нагружении, когда ω → ∞, модуль упругости называется адиабатическим и обозначается k _а.

На рис. 1.4 показаны фазовые порт-реты циклической деформации жидкости при медленном (график 1) и быстром (гра-фик 2) нагружении.

 

Рис. 1.4. Фазовые портреты деформации жидкости

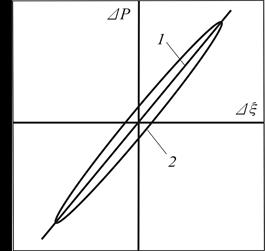
Зависимости изменения давления ΔР при изменении относительной деформации Δξ заданного объема жидкости:

существенно отличаются: при медленном нагружении замкнутого объема давлением фазовый сдвиг в зависимости ΔР = f (Δξ) не проявляется. Если циклическое нагружение происходит с большой частотой, возникает запаздывание деформации относительно давления, ее вызывающего и линейная функция 1 трансформируется в гистерезисную петлю 2, рис. 1.4.

Этот эффект обусловлен объемной вязкостью жидкости, проявляю-щейся при сжатии и не связанной с тангенциальной вязкостью при относи-тельном движении ее частиц. Именно объемная вязкость вызывает сдвиг по фазе между объемной деформацией и давлением.

Аналогичное явление имеет место в гибких резино-кордовых рукавах гидросистем, внутренняя резиновая обкладка которых при циклическом сжатии ведет себя так же, как и жидкость, содержащая Г -фазу гидроприводов зависимость объемного модуля упругости.

Гистерезис учитывают при расчете переходных процессов, для анализа динамических характеристик, при резонансных явлениях и в других спе-циальных задачах.

 

 

Температурное расширение

Температурное расширение – это относительное изменение объема жидкости, возникающее при увеличении температуры при постоянном давлении. Оно характеризуется коэффициентом температурного расширения, 1/°С:

(1.10)

 

Рассматривая конечное приращение:

ΔV = V – V ₁

и принимая β _t постоянным, получим зависимость для определения объема, занимаемого нагретой жидкостью:

(1.11)

Очевидно, что при нагревании жидкости, не только ее объем, но и плотность будут изменяться.

Приведенная ниже зави­симость, называемая формулой Менделеева, позволяет рассчитать плотность жидкости при заданном значении ее температуры Т, °С:

(1.12)

где ρ ₂₀ – плотность жидкости при 20 °С и нормальном атмосферном дав-лении, Т ₀ – исходная температура, °С.

На плотность капельных жидкостей изменение температуры оказывает незначительное влияние и чаще всего это свойство в инженерных расчетах не учитывают.

Так как газы обладают значительно меньшей плотностью, чем жидкости, то влияние температуры и давления на их плотность, и в частности на плотность воздуха, проявляется гораздо более существенно. При расчете пневмосистем для определения плотности воздуха при любой температуре и давлении пользуются формулой:

(1.13)

где Р ₀ и Т ₁ – давление и температура при нормальных условиях (Т ₁ = 293 °К, Р ₀ = 101325 Па), ρ ₀ – плотность воздуха при нормальных условиях (1,26 кг/м³), Т ₂ – заданная абсолютная температура.

 

 

Сопротивление растяжению

Тщательно очищенная и дегазированная вода способна кратковременно сопротивляться растяжению с напряжением 23…38 МПа, но в реальных условиях этого не происходит, поэтому принято считать, что жидкости не работают на растяжение.

 

Поверхностное натяжение

Силы поверхностного натяжения возникают на поверхностях раздела жидкости и газа. Именно они придают сферическую форму объемам жидкос-ти и вызывают в них небольшое повышение давления. Но оно заметно сказывается лишь при малых объемах и для сферического объема опреде-ляется формулой:

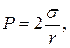(1.14)

где σ – коэффициент поверхностного натяжения жидкости (Н/м), r – радиус сферы.

Например для воды, при температуре 20 ºС, коэффициент поверхностного натяжения равен 73·10^-3, для спирта – 22,5·10^-3, для ртути – 460·10^-3 и т. д.

С увеличением температуры силы поверхностного натяжения слабеют.

Из-за этих сил в тонких трубках поверхность жидкости имеет либо вогнутую (для смачивающих жидкостей), либо выпуклую (для не смачиваю-щих жидкостей) формы.

Особое значение силы поверхностного натяжения имеют при исследо-вании жидкостей в процессах распыления.

 

Вязкость жидкости

Вязкость жидкостей – это свойство сопротивляться сдвигу (скольже-нию) ее слоев и оно противоположно текучести. Здесь рассматривается только тангенциальная вязкость, проявляющаяся при относительном дви-жении ее частиц.

Вязкость по Ньютоновой модели возникает из-за действия внутренних сил трения между движущимися слоями, определяемой по формуле, Н:

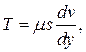(1.15)

где s – площадь слоев жидкости или стенки, соприкасающейся с жидкостью, μ – коэффициент динамической вязкости, dv – приращение скорости, соответствующее приращению координаты dy.

Коэффициент динамической вязкости равен, Н·с/м²:

(1.16)

где τ – касательное напряжение в жидкости.

При течении реальной жидкости вдоль твердой стенки происходит торможение потока, обусловленное вязкостью. Скорость снижается по мере уменьшения расстояния y от стенки вплоть до v = 0 при y = 0, а между слоями происходит проскальзывание, сопровождающееся возникновением касательных напряжений τ из-за сил трения, рис. 1.5.

Внесистемная единица измерения динамической вязкости – Пуаз:

1 П = 0,1 Па·с = 0,0102 кгс·с/м².

Рис. 1.5.

Профиль скоростей при течении вязкой жидкости вдоль твердой стенки

 

Отношение коэффициента динамической вязкости к плотности жидкости называется кинематической вязкостью, м²/с:

Величина ν, равная 1 см²/с называется стоксом (Ст).

В системе СИ кинематическая вязкость имеет размерность м²/с:

0,01 Ст = 1 сСт = 10^-4 м²/с.

Вязкость жидкостей уменьшается при увеличении температуры в соответствии с формулой:

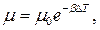(1.17)

где μ ₀ – динамическая вязкость в начальном состоянии, е – основание натурального логарифма (2,718), ΔТ – изменение температуры, β – коэффициент, зависящий от вида жидкости, 1/°С. Для минеральных масел значения β лежат в пределах 0,02…0,03.

На рис. 1.6-а показаны зависимости кинематической вязкости различ-ных жидкостей от температуры.

 

а. б.

Рис. 1.6. Зависимость кинематической вязкости от температуры (а), зависимость относительной вязкости минерального масла от давления (б)

 

Вязкость любой капельной жидкости по мере ее нагревания умень-шается, хотя графики этих зависимостей для разных жидкостей совпадают только качественно.

Воздух и другие газы при нагревании ведут себя противоположно: с увеличением температуры их вязкость увеличивается, рис. 1.6-а. Здесь вязкость обусловлена беспорядочным тепловым движением молекул, интенсивность которого при повышении температуры возрастает.

Вязкость зависит и от давления, но эта зависимость существенно про-является лишь при относительно больших его изменениях:

μ = μ ₀е ^{α ΔР} , (1.18)

где μ ₀ – динамическая вязкость при исходном давлении, α – коэффициент, зависящий от вида жидкости. Для минеральных масел он равен 0,02…0,03 (м²/Н); нижний предел соответствует высоким температурам, верхний – низким. ΔР – изменение давления.

На рис. 1.6-б показаны зависимости относительной динамической вязкости от давления для минеральных масел. Как видно из графиков лишь при Р > 40 МПа вязкость начинает существенно возрастать, поэтому в большинстве инженерных расчетов влияние давления на вязкость не учитывают.

 

 

Испаряемость жидкости

Испаряемость свойственна всем капельным жидкостям, а интен-сивность их испарения зависит от температуры, площади испарения, давления, и скорости движения воздуха над свободной поверхностью жидкости.

Температура кипения характеризует испаряемость при атмосферном давлении: чем выше температура кипения, тем меньше испаряемость жидкости.

В гидросистемах испарение жидкостей происходит в замкнутых объемах, поэтому основной характеристикой является давление насыщенных паров Р _н.п. Чем больше давление насыщенных паров при данной температуре, тем больше испаряемость жидкости. При нагревании жидкостей значение Р _н.п увеличивается, но у каждой жидкости немного по-другому.

На рис. 1.7 показаны зависимости давления насыщенных паров неко-торых жидкостей

от температуры.

 

Рис. 1.7. Зависимость давления насыщенных паров жидкостей от температуры

 

Давление Р _н.п отсчитывает-ся от абсолютного нуля, рис. 1.1, и чем оно больше, тем меньше уровень допустимого разряжения в резервуаре или трубопроводе, при котором жидкость будет оставаться однофазной средой. Если жидкость нагрета, то по сравнению с холодной, давление ее насыщенного пара будет больше, а уровень допустимого разряжения – меньше. Эту взаимосвязь можно отразить простой формулой, вытекающей их схемы, показанной на рис. 1.1:

Р_раз = Р_а – Р _н.п.

Если т. А (давление насыщенных паров) окажется в области разряже-ния, то в жидкости образуются мельчайшие пузырьки, наполненные ее пара-ми. Вместе с парами происходит выделение растворенных в жидкости газов (Р -фаза), образуется сплошная двухфазная среда, которая жидкостью уже не является и обладает совсем другими свойствами. Такая среда не может выполнять функцию рабочего тела при передаче энергии в гидросистемах, так как выделение газовоздушной составляющей прово-цирует кавитацию.

Кавитация проявляется при движении жидкости. Часто она возникает во всасывающих трубопроводах насосов, а так же в местных сопротивлениях трубопроводов, где поток жидкости претерпевает локальное сужение с последующим расширением: в кранах, вентилях, задвижках, диафрагмах, дросселях и др.

Если диаметр всасывающего трубопровода 3, рис. 1.8, из-за неверного подбора чрезмерно мал, или произошло критическое засорение фильтра 4, или, по какой-то причине расход насоса 1 чрезмерно возрос, то разряжение во всасывающем трубопроводе станет настолько сильным, что точка А (рис. 1.1) окажется в зоне разряжение и будет иметь место неравенство:

Р_а – Р_раз < Р _н.п.

Рис. 1.8. Схема, поясняющая возникновение кавитации в насосе

 

В этом случае во всасывающем трубопроводе жидкость разорвется и станет двухфазной средой, заполняя рабочие камеры насоса на такте всасывания. При переходе насоса в такт нагнетания, жидкость в его рабочих камерах соединится в напорным трубопроводом 2, находящимся под давлением Р _н, намного превышающим атмосферное давление Р _а, произойдет мгновенное схлопывание каверн (мельчайших пузырьков) и конденсация паров жидкости, что сопровождается многочисленными гидроударами и значительным локальным повышением давления.

Таким образом, кавитация, это процесс, состоящий из двух стадий: выделения растворенных газов и насыщенных паров с последующим схлопыванием образовавшихся каверн в области высокого давления. Этот процесс сопровождается сильным шумом и вибрацией и является разрушительным. В рабочих камерах насоса, его напорной полости и в прилегающей части напорного трубопровода происходит быстрый эрозионный износ стенок.

Работа насосов в режиме кавитации недопустима.

 

 

Облитерация

Облитерация свойственна в основном минеральным маслам, применя-ющимся в гидросистемах машин. Жидкости, полученные из нефти склонны к отложению смолистых осадков с течением времени. Когда эти отложения которые происходят на стенках тонких отверстий и щелей (размером нескольких микрометров), проходное сечение канала уменьшается, а иногда и полностью заращивается. Этому способствуют загрязнения, всегда присутствующие в жидкостях.

Нарушается стабильность расхода жидкости через эти каналы, увеличи-ваются усилия, необходимые для перемещения сопрягаемых деталей.