ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ
ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ
ЛУГАНСКОЙ НАРОДНОЙ РЕСПУБЛИКИ
«ЛУГАНСКИЙ НАЦИОНАЛЬНЫЙ УНИВЕРСИТЕТ
ИМЕНИ ВЛАДИМИРА ДАЛЯ»
Кафедра прикладной математики
Математическое моделирование
О Т Ч Ё Т
О выполнении практической работы № 1
НАХОЖДЕНИЕ ОПТИМАЛЬНОГО ПУТИ В СЕТИ
Вариант № 0
Выполнил: студент группы
ФИО________________________
Дата сдачи____________________
Оценка______________________________
Проверил___________________________
Луганск, 2020
Выполнение работы
1. Найти минимальный путь сети от узла 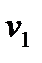 до узла
до узла  по алгоритму Дейкстры, если задана матрица длин дуг
по алгоритму Дейкстры, если задана матрица длин дуг
 .
.
Решение. Выполним для наглядности геометрическое изображение графа

|

|

|

|
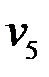
|
Протокол работы алгоритма будем оформлять в виде таблицы, которую построим в процессе решения.
Шаг 0. Все узлы помечаются: стартовый узел 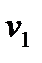 получает постоянную метку 0, все остальные узлы получают временные метки
получает постоянную метку 0, все остальные узлы получают временные метки  :
:
 ,
,  .
.
Эти значения заносим в нулевую строку таблицы.
Начертим для наглядности геометрическое изображение графа на шаге 0:

|

|

|

|
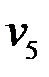
|

|

|

|

|
| 0 |
Шаг 1. Для узлов  с временными метками, достижимых из узла
с временными метками, достижимых из узла  с постоянной меткой, обновляем метки:
с постоянной меткой, обновляем метки:
 ;
;
 ;
;
 ;
;
 .
.
Постоянную метку получает узел  .
.
Эти значения заносим в первую строку таблицы.
Начертим для наглядности геометрическое изображение графа на шаге 1:

|

|

|

|
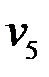
|

|

|
| 4 |
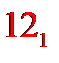
|
| 0 |
Шаг 2. Для узлов  с временными метками, достижимых из узла
с временными метками, достижимых из узла  с постоянной меткой, обновляем метки:
с постоянной меткой, обновляем метки:
 ;
;
 ;
;
 ;
;
 ;
;
 .
.
Постоянную метку получает узел  .
.
Эти значения заносим во вторую строку таблицы.
Начертим для наглядности геометрическое изображение графа на шаге 2:

|

|

|

|
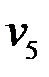
|
| 6 |

|
| 4 |

|
| 0 |
Шаг 3. Для узла  с временной меткой, который достижим из узла
с временной меткой, который достижим из узла 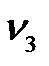 с постоянной меткой, обновляем метку:
с постоянной меткой, обновляем метку:
 ;
;

 .
.
Постоянную метку получает узел  .
.
Эти значения заносим в третью строку таблицы.
Начертим для наглядности геометрическое изображение графа на шаге 3:

|

|

|

|
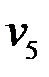
|
| 8 |
| 4 |

|
| 0 |
| 6 |
Шаг 4. Из узла  с постоянной меткой не выходит ни одна дуга.
с постоянной меткой не выходит ни одна дуга.
 ;
;
 .
.
Постоянную метку получает узел 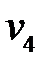 .
.
Эти значения заносим в четвертую строку таблицы.
Начертим для наглядности геометрическое изображение графа на шаге 4:

|

|

|

|
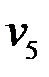
|
| 8 |
| 4 |
| 12 |
| 0 |
| 6 |
Таблица.
| Узлы Шаги | 
| 
| 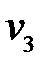
| 
| 
|
| 0 | 
| 
| 
| 
| |
| 0 | 4 | 
| 
| 
| |
| 0 | 4 | 6 | 
| 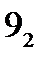
| |
| 0 | 4 | 6 | 
| 8 | |
| 0 | 4 | 6 | 12 | 8 |
Все узлы получили постоянные метки. Алгоритм завершен:
 ,
,  ,
,  ,
,  .
.
2) Чтобы найти минимальный путь от узла  до узла
до узла 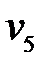 , используем временные индексы в постоянных метках: у узла
, используем временные индексы в постоянных метках: у узла  –
–  , у узла
, у узла  –
–  , у узла
, у узла  –
–  . Итак, минимальный путь от
. Итак, минимальный путь от  до
до  есть
есть  :
:  ,
,  ,
,  ,
,  . Его длина
. Его длина
 .
.
2. Найти минимальный путь сети от узла  до узла
до узла  по алгоритму Беллмана–Мура, если задана матрица длин дуг
по алгоритму Беллмана–Мура, если задана матрица длин дуг

Решение. 1) Начертим для наглядности геометрическое изображение графа

|

|

|

|
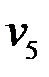
|
| –8 |

|
| –7 |
Этап 1. Нахождение длин кратчайших путей от узла 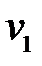 до всех остальных узлов графа.
до всех остальных узлов графа.
Шаг 0. Все узлы помечаются: стартовый узел  получает постоянную метку 0, все остальные узлы получают временные метки
получает постоянную метку 0, все остальные узлы получают временные метки  :
:
 ,
,  ,
, 
Шаг 1.
а) Удаляем из очереди  узел, находящийся в самом начале очереди.
узел, находящийся в самом начале очереди.

б) Для узла  с временными метками, досягаемого из узла
с временными метками, досягаемого из узла  корректируем метки:
корректируем метки:
 , бб) 4<∞;
, бб) 4<∞;
бв) Корректировка очереди:  ,
,  нужно было поставить в конец очереди, но
нужно было поставить в конец очереди, но  было пустым, поэтому конец очереди совпал с началом.
было пустым, поэтому конец очереди совпал с началом.
б)  , бб)
, бб)  ;
;
бв) Корректировка очереди:  .
.
Шаг 2. а) Удаляем из очереди  узел, находящийся в самом начале очереди:
узел, находящийся в самом начале очереди:  .
.  .
.
б)  , бб) 11<∞;
, бб) 11<∞;
бв) 
б)  , бб) –4<6;
, бб) –4<6;
бв)  . Узел
. Узел  нужно было поставить в начало очереди, но он уже там находится.
нужно было поставить в начало очереди, но он уже там находится.
б)  , бб) 10<∞;
, бб) 10<∞;
бв)  .
.
Шаг 3. а)  .
. 
б)  , бб) 4<11;
, бб) 4<11;
бв)  . Узел
. Узел  нужно поставить в начало очереди.
нужно поставить в начало очереди.
Шаг 4. а)  .
.  .
.
б)  , бб) 8<∞;
, бб) 8<∞;
бв)  .
.
Шаг 5. а)  .
.  .
.
б)  , бб) –3<5;
, бб) –3<5;
бв)  .
.
б)  , бб) 9<8;
, бб) 9<8;
бв)  .
.
Шаг 6. а)  .
.  .
.
б)  , бб) 0<8;
, бб) 0<8;
бв)  .
.  содержит только
содержит только  и он находится в начале очереди.
и он находится в начале очереди.
Шаг 7. а)  .
.  .
.
Конец первого этапа. Найдены минимальные расстояния до всех узлов от первого узла:

Этап 2. Построение кратчайшего пути от узла  до узла
до узла  .
.
Пусть  – конец пути.
– конец пути.  – множество узлов, непосредственно находящихся перед
– множество узлов, непосредственно находящихся перед  .
.
Шаг 1. 

Включаем дугу 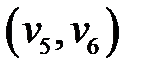 в кратчайший путь.
в кратчайший путь.
Шаг 2.  .
. 
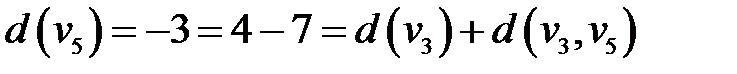 ,
,
 ,
,
 .
.
Включаем дугу 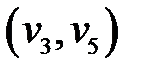 в кратчайший путь.
в кратчайший путь.
Шаг 3. 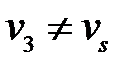 .
. 
 ,
,
 .
.
Включаем дугу  в кратчайший путь.
в кратчайший путь.
Шаг 4. 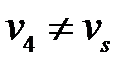 .
. 

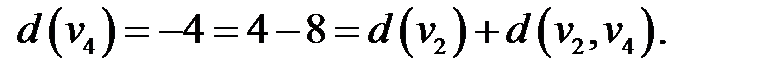
Включаем дугу  в кратчайший путь.
в кратчайший путь.
Шаг 5.  .
. 

Включаем дугу  в кратчайший путь.
в кратчайший путь.
Шаг 6.  . Алгоритм закончен. Искомый кратчайший путь от узла
. Алгоритм закончен. Искомый кратчайший путь от узла 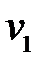 до узла
до узла  состоит из дуг:
состоит из дуг:

и имеет нулевой вес.