Определим рабочий ток, протекающий по каждому из участков сети по следующей формуле:
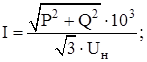 (2.1)
(2.1)
где Р – это значение активной мощности на каждом из участков сети, кВ∙А; Q – значение реактивной мощности протекающей по каждому из участков сети, кВар; Uн – номинальное напряжение сети, кВ.
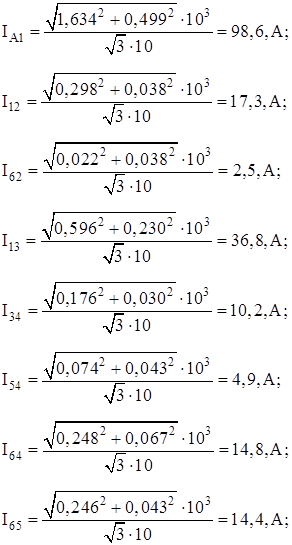

Определим сечение провода на каждом из участков сети по следующей формуле:
 (2.2)
(2.2)
где jэ – экономическая плотность тока, А/мм2. Примем jэ=1 [1].


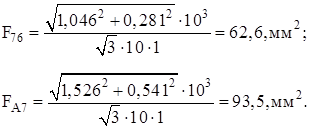
Выбираем ближайшие стандартные значения сечения проводов из [2], при это учитывая, что минимально допустимое сечение сталеалюминиевых проводов ЛЭП на напряжение 10 кВ по условиям механической прочности составляет 35 мм2.
Параметры сталеалюминиевых проводов сведём в табл. 2.1, учитывая, что температура воздуха составляет 250С. Погонное индуктивное сопротивление в таблице приведено при Dср=2 м. Так как напряжение сети 10 кВ, то погонные активные и реактивные проводимости можно не учитывать.
Таблица 2.1 – Параметры сталеалюминиевых проводов
| Участок сети | Марка провода | Rп, Ом/км | Хп, Ом/км | Рабочий ток, А | Допустимый длительный ток, А |
| A – 1 | АС-95/16 | 0,301 | 0,371 | 98,6 | |
| 1 – 2 | АС-35/6,2 | 0,850 | 0,403 | 17,3 | |
| 6 – 2 | АС-35/6,2 | 0,850 | 0,403 | 2,5 | |
| 1 – 3 | АС-35/6,2 | 0,850 | 0,403 | 36,8 | |
| 3 – 4 | АС-35/6,2 | 0,850 | 0,403 | 10,2 | |
| 5 – 4 | АС-35/6,2 | 0,850 | 0,403 | 4,9 | |
| 6 – 4 | АС-35/6,2 | 0,850 | 0,403 | 14,8 | |
| 6 – 5 | АС-35/6,2 | 0,850 | 0,403 | 14,4 | |
| 7 – 6 | АС-70/11 | 0,446 | 0,382 | 62,5 | |
| А – 7 | АС-95/16 | 0,301 | 0,371 | 93,5 |
Выбранные марки проводом подходят, так как длительно допустимые значения токов больше рабочих токов протекающих по участкам сети.
Найдём значения активных и реактивных сопротивлений участков сети по формулам:

Проведём аналогичные расчеты для остальных участков и полученные данные сведём в табл. 2.2.
Таблица 2.2 – Активные и индуктивные сопротивления участков сети
| Участок сети | Сопротивление, Ом | |
| Активное | Индуктивное | |
| A – 1 | 0,156 | 0,192 |
| 1 – 2 | 0,221 | 0,104 |
| 6 – 2 | 0,272 | 0,128 |
| 1 – 3 | 0,153 | 0,072 |
| 3 – 4 | 0,459 | 0,217 |
| 5 – 4 | 0,187 | 0,088 |
| 6 – 4 | 0,450 | 0,213 |
| 6 – 5 | 0,510 | 0,241 |
| 7 – 6 | 0,223 | 0,191 |
| А – 7 | 0,078 | 0,096 |
На данном этапе расчёт окончен.
Уточнение распределения мощностей (первая и вторая итерация)
Составим схему замещения с учётом сопротивлений участков сети (рис. 3.1):

Рис. 3.1. Схема замещения сети с учетом сопротивлений
Первая итерация
Рассчитаем потокораспределение с учётом, что напряжение во всех точках сети равно номинальному напряжению. Расчёт начнём от точки потокараздела находящейся в точке 5. Примем мощность в конце участка 6–5 равной значению мощности на этом участке при нулевой итерации:

Найдём мощность в начале участка 6–5:

Примем мощность в конце участка 4–5 равной значению мощности на этом участке при нулевой итерации:

Найдём мощность в начале участка 4–5:

Далее расчёт будем вести от точки потокараздела находящейся в точке 4. Примем мощность в конце участка 6–4 равной мощности на этом участке при нулевой итерации:

Мощность начала участка 6–4 равна:

Примем мощность в конце участка 3–4 равной мощности на этом участке при нулевой итерации:

Мощность в начале участка 3–4 равна:

Найдём мощность на участке:


Далее расчёт буде вести от точки потокараздела, находящейся в точке 2. Примем мощность в конце участка 1–2 равной мощности на этом участке при нулевой итерации:

Рассчитаем мощность в начале участка 1–2:

Найдём мощность в конце участка А-1 из первого закона Кирхгофа:
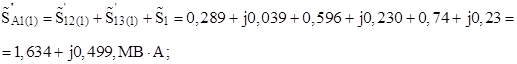
Примем мощность в конце участка 6–2 равной мощности на этом участке при нулевой итерации:

Мощность в начале участка 6–2 равна:

Найдём мощность в конце участка 7–6, используя первый закон Кирхгофа:

Мощность в начале участка 7–6 равна:

Найдём мощность в конце участка А-7:

Находим мощность в начале участка А-7:

На данном этапе расчёт окончен.
Вторая итерация
Расчёт на второй итерации проводится с учётом распределения напряжения. Расчёт проводим начиная от начали линии (от источника питания) до точек потокораздела в соответствие с рис. 3.1.
Примем мощность в начале участка А-1 из первой итерации:

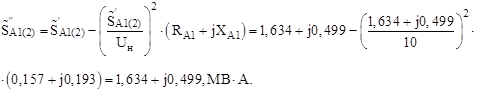
Определим напряжение в точке 1:

Рассчитаем мощность в начале участка 1–2, учитывая распределение мощностей при первой итерации:
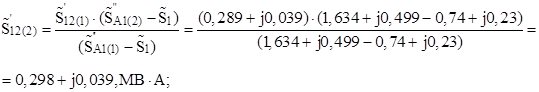

Определим напряжение в точке 2:

Мощность в начале участка 1–3 определим пользуясь первым законом Кирхгофа:


Определим напряжение в точке 3:



Найдём мощность в начале участка 3–4, используя первый закон Кирхгофа:

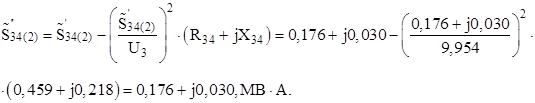
Определим напряжение в точке 4:

Примем мощность в начале участка А-7 равной мощности на это участке при нулевой итерации:



Определим напряжение в точке 7:

По первому закону Кирхгофа найдём мощность в начале участка 7–6:


Определим напряжение в точке 6:
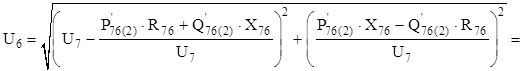


Определим мощности в начале участков 6–2 и 6–4 с учётом распределения мощностей при первой итерации:

Определим значение мощности, протекающей в начале участка 6–5 по первому закону Кирхгофа:


Найдём напряжение в точке 5:

Найдём мощность, протекающую в начале участка 5–4:


Все полученные в результате расчёта уточнённые значения мощностей сведём в табл. 3.1., а значения напряжений в узлах сети в табл. 3.2.
Таблица 3.1 – Уточнённые значения мощностей
| Участок сети | 
| 
|
| А-1 | 
| 
|
| 1–2 | 
| 
|
| 1–3 | 
| 
|
| 3–4 | 
| 
|
| А-7 | 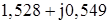
| 
|
| 7–6 | 
| 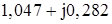
|
| 6–2 | 
| 
|
| 6–4 | 
| 
|
Таблица 3.2 – Значения напряжения в узлах сети
| Номер узла | А | |||||||
| U, кВ | 9,965 | 9,958 | 9,954 | 9,945 | 9,940 | 9,954 | 9,983 |
Уточним сечения проводов, используя формулу (2.2).

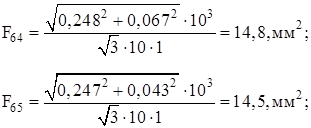

Выбираем ближайшие стандартные значения сечений проводов. Марки выбранных проводов для каждого из участков сети приведены в табл. 3.3.
Таблица 3.3 – Марки проводов по участкам сети
| Участок сети | Марка проводов | Допустимый длительный ток, А |
| A – 1 | АС-95/16 | |
| 1 – 2 | АС-35/6,2 | |
| 6 – 2 | АС-35/6,2 | |
| 1 – 3 | АС-35/6,2 | |
| 3 – 4 | АС-35/6,2 | |
| 5 – 4 | АС-35/6,2 | |
| 6 – 4 | АС-35/6,2 | |
| 6 – 5 | АС-35/6,2 | |
| 7 – 6 | АС-70/11 | |
| А – 7 | АС-95/16 |
Выбранные марки проводов совпадают с выбранными ранее марками (см. п. 2). В связи с этим без расчёта рабочих токов можно сделать вывод, что выбранные марки проводов, указанные в табл. 3.3. удовлетворяют условиям нагрева.