Равносильность уравнений.
Определение 1. Два уравнения с одной переменной f(x)=g(x) и p(x)=h(x) называют равносильными, если множества их корней совпадают.
Иными словами, два уравнения называют равносильными, если они имеют одинаковые корни, или если оба уравнения не имеют корней.
Определение 2. Если каждый корень уравнения f(x)=g(x) (1)
является в то же время корнем уравнения p(x)=h(x), (2)
то уравнение (2) называют следствием уравнения (1).
Очевидно следующее утверждение: два уравнения равносильны тогда и только тогда, когда каждое из них является следствием другого.
Теорема 1.
Если какой-либо член уравнения перенести из одной части уравнения в другую с противоположным знаком, то получится уравнение, равносильное данному.
Теорема 2.
Если обе части уравнения возвести в одну и ту же нечётную степень, то получится уравнение, равносильное данному.
Теорема 3.
Показательное уравнение af(x)=ag(x), где a>0, a≠1, равносильно
уравнению f(x)=g(x).
Определение 3.
Областью определения уравнения f(x)=g(x) или областью допустимых значений переменной (ОДЗ) называют множество тех значений переменной x, при которых одновременно имеют смысл выражения f(x) и g(x).
Теорема 4.
Если обе части уравнения f(x)=g(x) умножить на одно и то же выражение h(x), которое:
a) имеет смысл всюду в области определения (в области допустимых значений) уравнения f(x)=g(x);
б) нигде в этой области не обращается в 0
— то получится уравнение f(x)⋅h(x)=g(x)⋅h(x), равносильное данному.
Следствие теоремы 4.
Если обе части уравнения умножить или разделить на одно и то же отличное от нуля число, то получится уравнение, равносильное данному.
Теорема 5.
Если обе части уравнения f(x)=g(x) неотрицательны в области определения уравнения, то после возведения обеих его частей в одну и ту же чётную степень n получится уравнение, равносильное данному: f(x)n=g(x)n.
Теорема 6.
Если f(x)>0 и g(x)>0, то логарифмическое уравнение logа f(x)=logа g(x), где a>0, a≠1, равносильно уравнению f(x)=g(x).
Определение. Посторонние корни – это корни полученного в результате проведения преобразований уравнения-следствия, не являющиеся корнями исходного уравнения.
Пример. Рассмотрим уравнение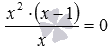 
и следствие этого уравнения x·(x−1)=0, полученное в результате замены выражения 
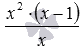тождественно равным ему выражением x·(x−1). Исходное уравнение имеет единственный корень 1. Уравнение, полученное в результате проведения преобразования, имеет два корня 0 и 1. Значит 0 – это посторонний корень для исходного уравнения.
Если для получения уравнения-следствия не использовать никакие «экзотические» преобразования, а использовать только основные преобразования уравнений, то посторонние корни могут возникнуть лишь по двум причинам:
- из-за расширения ОДЗ;
- из-за возведения обеих частей уравнения в одну и ту же четную степень.
Здесь стоит напомнить, что расширение ОДЗ в результате преобразования уравнения в основном происходит:
- при сокращении дробей;
- при замене нулем произведения с одним или несколькими нулевыми множителями;
- при замене нулем дроби с нулевым числителем;
- при использовании некоторых свойств степеней, корней, логарифмов;
- при использовании некоторых тригонометрических формул;
-при умножении обеих частей уравнения на одно и то же выражение, обращающееся в нуль на ОДЗ для этого уравнения;
- при освобождении в процессе решения от знаков логарифмов.
Из-за чего могут быть потеряны корни уравнения?
Существуют три основные причины потери корней:
- сужение ОДЗ при замене выражения тождественно равным ему выражением,
- замена выражения не тождественно равным ему выражением,
- некорректное освобождение от внешней функции.
Точнее, главная причина одна – некорректное проведение преобразований при решении уравнений.
Задание:
1. Определить являются ли данные уравнения равносильными?
1,7x - 34 = 0,7x - 5
17x - 340 = 7x – 50
2. Определить являются ли данные уравнения равносильными?
x2 + 4 = 0
5,1x2 = - 123, 67
3. Определить являются ли данные уравнения равносильными?
х – 2 = 4
х2 = 36