Связь бинома Ньютона с треугольником Паскаля

Треугольник Паскаля

Для того, чтобы получить треугольник Паскаля, перепишем Таблицу 1 из раздела «Формулы сокращенного умножения: степень суммы и степень разности» в следующем виде (Таблица П.):

Таблица П. – Натуральные степени бинома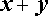

№	Степень	Разложение в сумму одночленов
...	...	...

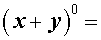
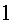
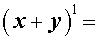
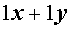
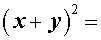
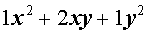
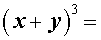
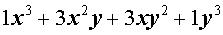
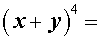
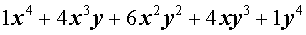
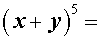
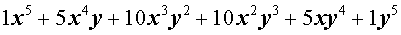
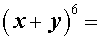
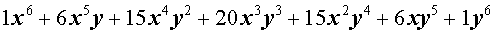
Теперь, воспользовавшись третьим столбцом Таблицы П., составим следующую Таблицу - Треугольник Паскаля:

Таблица - Треугольник Паскаля

№	Треугольник Паскаля
...	...

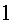
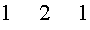
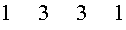
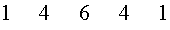
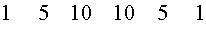
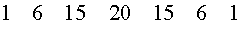
На всякий случай напомним, что Блез Паскаль – это знаменитый физик и математик, живший во Франции более трех веков назад.

В треугольнике Паскаля каждая строка соответствует строке с тем же номером в Таблице П. Однако в каждой строке треугольника Паскаля, в отличие от Таблицы П., записаны только коэффициенты разложения в сумму одночленов соответствующей степени бинома .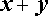

Заполнив сначала строки треугольника Паскаля с номерами 0 и 1, рассмотрим строки с номерами 2 и далее.

Основным свойством треугольника Паскаля, позволяющим последовательно, начиная со строки с номером 2, заполнять его строки, является следующее свойство:

Каждая из строк, начиная со строки с номером 2, во-первых, начинается и заканчивается числом 1, а, во-вторых, между числами 1 стоят числа, каждое из которых равно сумме двух чисел, стоящих над ним в предыдущей строке.

Действительно, число 2, стоящее в строке с номером два, равно сумме чисел 1 плюс 1, стоящих в первой строке. Точно так же, числа 3 и 3, стоящие в строке с номером три, равны соответственно сумме чисел 1 плюс 2 и сумме чисел 2 плюс 1, стоящих во второй строке.

Также и для других строк.

Таким образом, свойство треугольника Паскаля позволяет, заполнив одну из строк, легко заполнить и следующую за ней, т.е. получить необходимые коэффициенты разложения в сумму одночленов следующей степени бинома .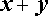

Пример. Написать разложение вида:

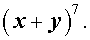
Решение. Воспользовавшись строкой треугольника Паскаля с номером 6 и применив основное свойство треугольника Паскаля, получим строку с номером 7:

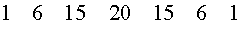
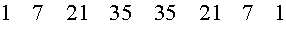
Следовательно,

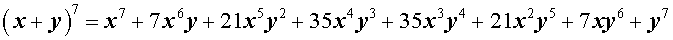
Бином Ньютона

Формула бинома Ньютона

В Таблице 1 из раздела «Формулы сокращенного умножения» приведены формулы для натуральных степеней бинома

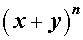
в случаях, когда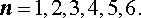

В настоящем разделе рассматривается общий случай этой формулы, т.е. случай произвольного натурального значения .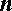

Материал настоящего раздела близко связан с материалом разделов «Формулы сокращенного умножения: степень суммы и степень разности», «Треугольник Паскаля» и «Комбинаторика: размещения и сочетания».

Утверждение. Для любого натурального числа 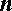и любых чисел 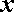и 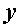справедлива формула бинома Ньютона:

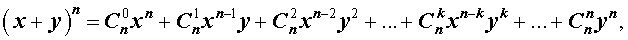
(1)

где

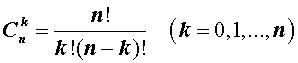
(2)

- числа сочетаний из 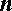элементов по 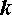элементов.

В формуле (1) слагаемые

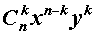
называют членами разложения бинома Ньютона, а числа сочетаний 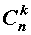- коэффициентами разложения или биномиальными коэффициентами.

Если в формуле (1) заменить 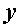на 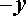, то мы получим формулу для 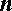- ой степени разности:

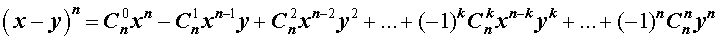
Связь бинома Ньютона с треугольником Паскаля

Напомним, что треугольник Паскаля имеет следующий вид:

№	Треугольник Паскаля
...	...

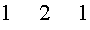
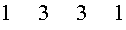
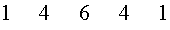
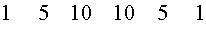
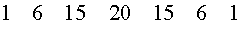
Поскольку числа, составляющие треугольник Паскаля, являются биномиальными коэффициентами, то треугольник Паскаля можно переписать в другом виде:

№	Треугольник Паскаля
...	...
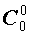
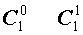
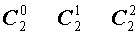
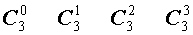
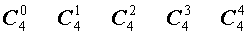
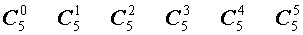
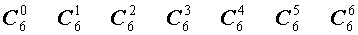