Сначала для решения предложенной задачи необходимо разработать математическую модель, включающую целевую функцию, задающую взаимосвязь целевых критериев с варьируемыми параметрами и систему ограничений, налагаемых на варьируемые параметры.
Введем следующие обозначения:
х1 - содержание известняка (в фунтах) в смеси;
х2 - содержание зерна (в фунтах) в смеси;
х3 - содержание соевых бобов (в фунтах) в смеси.
В качестве целевой функции выступает общая стоимость смеси, определяемая по формуле:
0,04х1 + 0,15х2 + 0,40х3 → min
Минимальный общий вес смеси, ежедневно расходуемый на кормление 20000 цыплят равен 20000 фунтов, следовательно необходимо ввести ограничение:
х1 + х2 + х3 ≥ 20000
Кроме того, налагаются ограничения на питательность смеси. Так, содержание кальция в смеси ограничено 0,8 - 1,2%, следовательно:
0,38х1 + 0,001х2 + 0,002х3 ≥ 0,008 (х1 + х2 + х3)
0,38х1 + 0,001х2 + 0,002х3 ≤ 0,012 (х1 + х2 + х3)
Преобразовав неравенства, получим:
0,372х1 - 0,007х2 - 0,006х3 ≥ 0
0,368х1 - 0,011х2 - 0,010х3 ≤ 0
Аналогичным образом записываются другие ограничения по питательности смеси. Окончательная математическая модель задачи имеет вид:
 0,04х1 + 0,15х2 + 0,40х3 → min
0,04х1 + 0,15х2 + 0,40х3 → min
0,372х1 - 0,007х2 - 0,006х3 ≥ 0
0,368х1 - 0,011х2 - 0,010х3 ≤ 0
0,220х1 + 0,130х2 - 0,280х3 ≤ 0
0,050х1 + 0,030х2 - 0,030х3 ≥ 0
х1 ≥ 0
х2 ≥ 0
х3 ≥ 0
Для решения задачи в MS Excel требуется занести варьируемые параметры в ячейки таблицы, задать формулу, отражающую целевую функцию и формулы, задающие левые части ограничений в форме неравенств.
1 Разработать макет таблицы и занести в ячейки таблицы исходные данные и расчетные формулы.


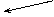

Рис. 13 Форматирование таблицы и занесение исходных данных
2 Для выполнения расчета выбрать пункт меню Сервис → Поиск решения. Если этот пункт отсутствует в меню, то в пункте меню Сервис → Надстройки сделать доступной (пометить) надстройку «Поиск решения».
3 В окне поиска решения задать ссылку на целевую функцию в поле ввода «Установить целевую». Вводить целевую функцию можно либо непосредственно в поле ввода, либо установить курсор в соответствующее поле ввода и щелкнуть по ячейке таблицы, значение которой будет использовано в качестве целевой функции.
4 Указать критерий оптимизации (минимизация или максимизация) целевой функции. В нашем примере затраты должны быть минимальными.
5 Задать варьируемые параметры в поле «Изменяя ячейки». Также, как и при задании целевой функции, можно воспользоваться клавиатурой или мышью.
6 Для добавления ограничений нажать на кнопку «Добавить» в блоке «Ограничения» окна поиска решения.










Рис. 14 Окно надстройки поиск решения
7 В открывшемся окне добавления ограничения занести в поле ввода «Ссылка на ячейку» адрес ячейки с правой частью ограничения, выбрать из списка знак неравенства (для этого надо щелкнуть по кнопке списка рядом с полем ввода знака неравенства) и в поле ввода «Ограничение» задать правую часть неравенства (константу или ссылку на ячейку).
8 Нажать кнопку «Добавить». При этом заданное ограничение будет перенесено в список ограничений окна поиска решения, но окно добавления ограничения не будет закрыто. В нем можно задать следующее ограничение. После ввода всех ограничений нажать на кнопку ОК для возврата в окно поиска решения.
 |







Рис. 15 Окно добавления ограничения
9 Можно дополнительно установить параметры оптимизации. Для этого надо нажать кнопку «Параметры» в окне поиска решения.
10 В открывшемся окне параметров можно установить ограничение времени расчета, предельное число итераций (шагов цикла поиска решения), погрешность и сходимость, а также выбрать метод оптимизации.
11 После того, как параметры заданы, нажать кнопку ОК для возврата в окно поиска решения.





Рис. 16 Окно параметров поиска решения
12 Для решения оптимизационной задачи необходимо нажать кнопку «Выполнить» в окне поиска решения.
13 После выполнения расчета на появится окно диалоговое, в котором отображаются результаты поиска решения (решение найдено или значения целевой ячейки не сходятся). В зависимости от результата можно сохранить найденное решение или восстановить исходные значения варьируемых параметров.
14 Кроме того, можно на отдельных листах рабочей книги сохранить отчеты по результатам оптимизации, устойчивости (содержит сведения о чувствительности решения к малым изменениям в формуле) или пределах (отображает целевую ячейку и список влияющих ячеек модели, их значения, а также нижние и верхние границы).
15 Для сохранения результатов расчета нажать кнопку ОК в диалоговом окне.







Рис. 17 Окно результатов поиска решения
16 На рабочем листе будут сохранены найденные значения варьируемых параметров и оптимальное значение целевой функции.




Рис. 18 Результаты оптимизационного расчета
17 Сохранить результаты работы в файле. Воспользоваться пунктом меню Файл → Сохранить.
ДОПОЛНИТЕЛЬНЫЕ ЗАДАНИЯ
1 Используя справочную систему MS Excel познакомьтесь с методами оптимизации, реализованными в пакете поиска решения.
2 Изучите примеры использования процедуры поиска решения, которые находятся в файле Solvsamp.xls, расположенном в папке Office\Samples.
ЗАДАНИЯ ПО ВАРИАНТАМ
1 Промышленная фирма производит изделие, представляющее собой сборку из трех различных узлов. Эти узлы изготовляются на двух заводах. Из-за различий в составе технологического оборудования производительность заводов по выпуску каждого из трех видов узлов неодинакова. Исходные данные, характеризующие как производительность заводов по выпуску каждого из узлов, так и максимальный суммарный ресурс времени, которым в течение недели располагает каждый из заводов для производства этих узлов:
| Завод | Максимальный недельный фонд времени, ч | Производительность, узел/ч | ||
| Узел 1 | Узел 2 | Узел 3 | ||
Идеальной является такая ситуация, когда производственные мощности обоих заводов используются таким образом, что в итоге обеспечивается выпуск одинакового количества каждого из видов узлов. Однако этого трудно добиться из-за различий в производительности заводов. Более реальная цель состоит в том, чтобы максимизировать выпуск изделий, что, по существу, эквивалентно минимизации дисбаланса, возникающего вследствие некомплектности поставки по одному или двум видам узлов.
Возможный объем производства каждого из трех видов узлов зависит от того, какой фонд времени выделяет каждый завод для их изготовления.
Требуется определить еженедельные затраты времени (в часах) на производство каждого из трех видов узлов на каждом заводе, не превышающие в сумме временные ресурсы каждого завода и обеспечивающие максимальный выпуск изделий.
2 Предприятие производит три вида конфет - «Пилот», «Север» и «Айсберг». Известно, что реализация килограмма конфет «Пилот» дает прибыль 9 руб., «Север» - 10 руб. и «Айсберг» - 16 руб.
Конфеты можно производить в любых количествах (сбыт обеспечен), но запасы сырья ограничены.
Нормы расхода сырья на производство 1 кг конфет:
| Сырье | Нормы расхода сырья | Запасы сырья | ||
| «Пилот» | «Север» | «Айсберг» | ||
| Сахар | 0,18 | 0,15 | 0,12 | |
| Какао | 0,06 | 0,04 | 0,08 | |
| Ароматизатор | 0,05 | 0,03 | 0,03 |
Необходимо определить, каких конфет и сколько килограмм необходимо произвести, чтобы общая прибыль от реализации была максимальной.
3 Фирма изготовляет два типа электрических выключателей – «Солярис» и «Комби». Прибыль от реализации одного выключателя составляет, соответственно, 4 руб. и 3 руб. На изготовление выключателя типа «Солярис» требуется в три раза больше рабочего времени, чем на «Комби».
Если бы изготавливались выключатели только типа «Комби», то дневного рабочего времени хватило бы для изготовления 1000 выключателей. Поставка медного провода обеспечивает изготовление только 800 выключателей в день (любого типа). Для выключателей требуются специальные изоляторы. Их запасы обеспечивают дневной выпуск не более 400 выключателей типа «Солярис» и более 700 выключателей типа «Комби». Необходимо определить, сколько выключателей различного типа необходимо произвести, чтобы общая прибыль от реализации была максимальной.
Рекомендации: для решения оптимизационных задач используйте надстройку анализа (меню Сервис → Поиск решения).
4 Задача оптимального финансирования инвестиционного проекта. Промышленная организация заключила контракт со строительной компанией о строительстве нового цеха. В условиях контракта сказано, что промышленная организация должна выплатить строительной организации 60 д.е. в конце первого квартала и 100 д.е. в конце второго квартала. Для финансирования этого проекта промышленная организация создает фонд, причем деньги в инвестиционный фонд вкладываются только в начале первого квартала. При этом существует возможность вкладывать деньги в бескупонные облигации сроком на один квартал в начале первого квартала и в начале второго квартала. Эффективная доходность таких вложений составляет 3%, а уровень риска – 1. Также можно вкладывать деньги в бескупонные облигации в начале первого квартала сроком на пол года. Эффективная доходность таких вложений – 10%, уровень риска – 3. Требуется минимизировать начальные вложения в инвестиционный фонд. При этом средневзвешенный уровень риска в течение каждого из двух кварталов не должен превышать 2.
5 Задача оптимального выбора инвестиционных проектов. Фирма может выбрать один или несколько инвестиционных проектов из трех. Чистая текущая стоимость первого проекта равна 120 д.е., второго проекта – 160 д.е. и третьего проекта – 80 д.е. Каждый из этих проектов требует инвестиции в течении двух лет. Первый проект требует 90 д.е. инвестиций в течение первого года и 70 д.е. в течение второго года; второй проект – 100 д.е. в течение первого года и 80 д.е. в течение второго года; и третий проект – 60 д.е. в течение первого года и 40 д.е. в течение второго года. Для финансирования проектов фирма выделила 150 д.е. на первый год и 110 д.е. на второй год. Требуется отобрать проекты, суммарная чистая текущая стоимость которых максимальна, и при этом для каждого из двух лет суммарные инвестиции в проекты не превышают выделенных сумм.
6 Решите задачу № 5 при дополнительном условии, что третий проект может быть принят только в случае принятия второго проекта.
7 Решите задачу № 5 при дополнительном условии, что первый и второй проекты являются взаимоисключающими.
8 Решите задачу № 5 при дополнительном условии, что обязательно должен быть принят хотя бы один из второго и третьего проектов.
ВАРИАНТЫЛАБОРАТОРНЫХ РАБОТ
| № варианта | Лабораторные работы | |||
| № 1 | № 2 | № 3 | № 4 | |
СПИСОК РЕКОМЕНДУЕМОЙ ЛИТЕРАТУРЫ
1 Информатика: Учебник / Под ред. Проф. Н. В. Макаровой. – М.: Финансы и статистика, 1997.
2 Карлберг К. Бизнес-анализ с помощью Excel / Пер. с англ. – К.: Диалектика, 1997.
3 Додж М., Стинсон К. Эффективная работа с Microsoft Excel 2000. – СПб.: Питер, 1999.
4 Хэлворсон М., Янг М. Эффективная работа с Microsoft Office 2000 в целом. – СПб.: Питер, 2000.
5 Новиков Ф.А., Яценко А.Д. Microsoft Office 2000 в целом. – СПб.: ВХБ – Санкт-Петербург, 1999.