Цель работы: ознакомить студентов с видами представления исходных данных и обучить практическим навыкам визуализации многомерных данных в среде Statistica.
1 Основные сведения
1.1 Виды представления многомерных данных
Независимо от природы наблюдаемых явлений или процессов в большинстве ситуаций исходные данные представляются в виде матрицы (таблицы) объект-признак, где строками являются объекты, а столбцами ─ признаки. Под объектом подразумевается любой предмет изучения, например, страна, фирма, регион, студенческая группа и т. п. Признак определяет характеристики рассматриваемого объекта, например, если объектом исследования является фирма, то к числу признаков, ее характеризующих, можно отнести численность персонала, ежемесячный объем расходов и доходов, число контрагентов и другие характеристики. Каждый элемент такой матрицы Х обозначается как xij, где 
- номер объекта; 
- номер признака. Размерность этой матрицы составляет 
. Матрица Х описывает m объектов в терминах n признаков, причем значения m и n обычно достаточно велики. Считается, что для получения статистически достоверных результатов число объектов должно превышать число признаков в несколько раз.
При обработке многомерных данных следует учитывать дуализм представления, так как имеются возможности визуализации как объектов в пространстве признаков, так и признаков в пространстве объектов. Кроме представления исходных данных в виде матрицы объект-признак, имеются и другие возможности представления. Например, с помощью коэффициента корреляции между признаками, который вычисляется по формуле
где 
─ среднее значение произведения величин признаков xi, xk; 
, 
─ среднее значение признака xi, (xk); si (sk) ─ среднеквадратичное отклонение соответствующих признаков, можно представить исходные данные в виде матрицы признак-признак.
Эта матрица R в отличие от предыдущей имеет размерность 
. В каждой ячейке матрицы расположены значения коэффициента корреляции между соответствующими признаками; на диагонали матрицы стоят единицы, так как корреляция признака с самим собой максимальна и равна единице. Матрица симметрична относительно своей диагонали.
Сходство или различие между классифицируемыми объектами устанавливается в зависимости от метрического расстояния между ними. Если каждый объект описывается n признаками, то он может быть представлен как точка в n -мерном пространстве, и его сходство с другими объектами будет определяться как соответствующее расстояние. Указанное обстоятельство позволяет перейти к еще одному виду представления исходных данных, а именно, к матрице D объект-объект, представляющей собой таблицу расстояний между анализируемыми объектами. В этом случае в каждой ячейке матрицы находится величина расстояния, допустим, евклидова, рассчитываемого по формуле:
.
Здесь xij, xkj ─ значения j -го признака, соответственно, у i -го и k -го объектов.
На диагонали матрицы находятся нули, поскольку расстояние от точки до нее самой равно нулю. Элементы матрицы симметричны относительно диагонали.
Таким образом, исходные данные могут быть представлены в виде матриц трех типов:
· матрицы объект-признак;
· матрицы признак-признак;
· матрицы объект-объект.
1.2 Визуализация многомерных данных
Любое исследование многомерных данных невозможно без использования метода главных компонентов (ГК). Сущность этого метода заключается в снижении размерности данных путем определения незначительного числа линейных комбинаций исходных признаков, которые объясняют большую часть изменчивости данных в целом. Метод ГК связан с переходом к новой системе координат, которая является системой ортонормированных линейных комбинаций. Этот метод дает возможность по n исходным признакам объектов построить такое же количество ГК, являющихся обобщенными (агрегированными) признаками. На первый взгляд, такой переход не дает никакого преимущества в представлении данных, но существует возможность сохранения информации о рассматриваемых данных даже в том случае, если сократить количество вычисленных ГК. Кроме того, при сохранении двух или трех ГК реализуется возможность визуализации многомерных объектов в сокращенном признаковом пространстве. Метод ГК обладает рядом свойств, делающим его эффективным для визуализации структуры многомерных данных. Все они касаются наименьшего искажения геометрической структуры точек (объектов) при их проектировании в пространстве меньшей размерности.
Математическая модель ГК базируется на допущении, что значения множества взаимосвязанных признаков порождают некоторый общий результат. В этой связи при представлении исходных данных как раз и важна матрица признак-признак, в которой содержится вся информация о попарной связи между признаками.
Первым ГК набора первичных признаков Х=(х1,х2,…,хn) называется такая линейная комбинация этих признаков, которая среди прочих линейных комбинаций обладает наибольшей дисперсией. Геометрически это означает, что первый ГК ориентирован вдоль направления наибольшей вытянутости гиперэллипсоида рассеивания исследуемой совокупности данных. Второй ГК имеет наибольшую дисперсию рассеивания среди всех линейных преобразований, некоррелированных с первым ГК, и представляет собой проекцию на направление наибольшей вытянутости наблюдений в гиперплоскости, перпендикулярной первому ГК. Вообще, j–м ГК системы исходных признаков Х=(х1,х2,…,хn) называется такая линейная комбинация этих признаков, которая некоррелирована с (j-1) предыдущими ГК и среди всех прочих некоррелированных с предыдущими (j-1) ГК обладает наибольшей дисперсией. Отсюда следует, что ГК занумерованы в порядке убывания их дисперсий, т.е. 
, а это дает основу для принятия решения о том, сколько последних ГК можно без ущерба изъять из рассмотрения.
Решение задачи методом ГК сводится к поэтапному преобразованию матрицы исходных данных. Основные шаги метода показаны на схеме, приведенной на рис.1.
Рис. 1. Вычислительная схема метода главных компонентов
Прокомментируем этапы вычислений. В качестве исходных данных обычно выбирается матрица объект-признак Х. Поскольку характеристиками объектов могут служить признаки различной природы, то данные необходимо стандартизировать, т. е. провести центрирование (вычитание среднего значения) и нормирование (деление на среднеквадратичное значение) данных.
На следующем шаге вычисляется матрица корреляций R между признаками, т. е. осуществляется переход к матрице признак-признак. Диагональные элементы этой матрицы равны единице, а сама матрица симметрична относительно этой диагонали, так как rij=rji.
Далее определяется матрица собственных векторов В, которая, также, как и предыдущая, является квадратной и состоит из n строк и n столбцов. Компоненты каждого собственного вектора представлены в виде вектора-столбца, сумма квадратов составляющих которого вследствие ортогональности равна единице.
На следующем этапе проводится расчет матрицы собственных чисел Λ, которая в отличие от предыдущих матриц является диагональной, т. е. здесь только на диагонали матрицы находятся собственные числа: все прочие элементы матрицы равны нулю. Размерность этой матрицы, как и двух предыдущих, составляет 
. Каждое значение λj определяет дисперсию каждого ГК. Суммарное значение 
равняется сумме дисперсий исходных признаков. При условии стандартизации исходных данных 
На последнем шаге вычисляются ГК:
· с помощью матрицы Λ находятся два или три наибольших собственных числа (такой выбор обусловлен желанием визуализировать многомерные объекты в двумерной плоскости или трехмерном пространстве);
· по матрице В определяются собственные вектора (СВ), которые соответствуют выбранным собственным числам;
· найденные таким образом собственные вектора умножаются последовательно на строки исходной матрицы, формируя значения ГК для каждого объекта.
Например, при выборе только первых двух наибольших собственных чисел определяем соответствующие им составляющие СВ (два столбца матрицы В), которые перемножаем на строки матрицы Х.
Перемножение первого столбца матрицы В на первую строку матрицы Х даст значение первого ГК для первого объекта, умножение того же столбца на вторую строку определяет значение первого ГК для второго объекта, т.е.
Y1 = b11x11 +b21x12+... + bn1x1n,
где b11,b21,…, bn1 - компоненты первого СВ; x11,x12,…, x1n - первая строка матрицы данных объект-признак.
После выполнения таких же операций со вторым выбранным вектором, рассчитанным по формуле
Y2 = b12x21 +b22x22+... + bn2x2n,
получаем возможность построить все объекты в плоскости первых двух ГК, где их взаимное расположение позволяет сделать предварительные выводы о сходстве (различии) объектов.
2 Работа на компьютере
Выполнение данной работы производится с программным пакетом Statistica; версия 6.1.
2.1 Представление многомерных данных
1. Из папки Examples - Datasets открываем файл данных, озаглавленный Activities, в котором приведены различные характеристики образа жизни для 28 групп людей. В качестве активных переменных использовано семь видов социальной активности: work (работа), transport (транспорт), children (дети), household (домашний быт), shopping (покупки), personal care (личное время), meal (еда). Показателем является общее время, затраченное на данный вид деятельности представителями группы в часах. В качестве вспомогательных признаков выбраны: sleep (сон), TV (телевизор), leisure (досуг). В файл данных введена дополнительная переменная gender (пол), принимающая значения male (мужчины) и female (женщины). Для присвоения меток точкам на графиках добавлен группирующий признак geo. region (регион). Часть таблицы исходных данных приведена на рис.2.
Рис.2. Матрица объект-признак
2. Перейти к матрице признак – признак посредством следующих действий: в командной строке окна выбрать опцию Анализ, в которой указать позицию Основные статистики и таблицы. В открывшемся окне отметить Парные и частные корреляции и нажать OK. Далее выбрать первые семь переменных из первого списка. В итоге должна получиться матрица корреляций между признаками размерностью 7х7, вид которой показан на рис.3.
Рис.3. Матрица признак - признак
При обработке данных в этом случае строки с пропущенными данными исключаются из рассмотрения, поэтому из исходных 28 строк остается 23.
3. Перейти к матрице объект-объект следующими операциями: в командной строке окна выбрать опцию Анализ, в которой указать позицию Многомерный разведочный анализ и далее - Кластерный анализ - Иерархическая кластеризация, после чего нажать ОК. В открывшемся окне кластерного анализа на вкладке Дополнительно, в опции Объекты выбрать Наблюдения (строки) (рис.4), нажать ОК, далее отметить в окне те же 7 переменных и нажать ОК.
Рис.4. Окно кластерного анализа
В открывшемся окне Результаты иерархической кластеризации выбрать Матрицу расстояний, которая и представляет собой матрицу «объект-объект», размерностью 23х23. Часть этой таблицы приведена на рис.5.
Рис.5. Матрица объект-объект
Пользуясь такой матрицей, можно построить дендрограмму объединения объектов, сходных или различных по семи признакам. Для этого в окне Результаты иерархической кластеризации нажать клавишу Вертикальная дендрограмма, в результате чего приходим к графику, показанному на рис.6.
Полученная дендрограмма указывает порядок и уровень объединения объектов, сходных между собой, а также сформировавшиеся кластеры (группы) сходных объектов. В данном примере образовано 4 кластера.
Рис.6. Дендрограмма объектов
2.2 Метод главных компонентов
1. Из папки Examples - Datasets открываем тот же самый файл данных Activities.
2. В командной строке окна выбрать опцию Анализ, в которой указать позицию Многомерный разведочный анализ и далее - Анализ главных компонент и классификация. В стартовой панели модуля на вкладке Дополнительно нажать кнопку Переменные. В открывшемся окне Выберите переменные… в поле Переменные анализа выделить первые 7 переменных; в поле Вспомогательные - переменные sleep - leisure; в поле С основными наблюдениями - gender; в поле Группирующая - geo. region. После этих процедур окно Выберите переменные … принимает вид, показанный на рис. 7.
Рис.7. Окно выбора переменных
После нажатия ОК стартовая панель имеет вид, показанный на рис.8.
Рис.8. Стартовая панель после выбора переменных
Кроме того, на стартовой панели в поле Код для основных наблюдений указать значение переменной female. Здесь же в рамке Анализ основан на … выбрать опцию корреляцияхs, так как средние значения и дисперсии каждой переменной могут значительно различаться между собой. В рамке Удаление пропущенных данных указать опцию Замена средним, а в рамке Оценка дисперсии - опцию SS/ N-1, поскольку данных не очень много, и выбор другой опции может привести к смещенным оценкам дисперсии. После выбора этих опций нажать ОК.
3. В появившемся окне результатов анализа в информационной части указано количество основных и вспомогательных переменных и наблюдений (рис. 9).
Рис.9. Окно результатов анализа
После нажатия кнопки График каменистой осыпи на вкладке Переменные программа построит график изменения собственных чисел (СЧ) корреляционной матрицы, показанный на рис.10.
Рис.10. График изменения собственных чисел
Сами СЧ можно увидеть после нажатия кнопки Собственные значения в появившейся таблице (рис.11).
Рис.11. Собственные числа
Анализ графика и таблицы позволяет выбрать число выделяемых ГК. Например, по графику можно определить СЧ, начиная с которого график теряет свою кривизну, и убывание СЧ максимально замедляется. Из графика видно, что такими СЧ являются 2 или 3, поэтому число выделяемых ГК может быть равно 2 или 3. Выбрав число, равное 2, введем его в поле Число факторов (рис.8), после чего Качество представления изменит свое значение со 100% на 81% (рис.12).
Рис.12. Качество представления при двух факторах
Тот же самый вывод следует из таблицы рис.10, где в последнем столбце приведены значения накопленной суммы СЧ: видно, что при двух оставляемых в анализе СЧ эта сумма составляет примерно 81%. Следовательно, потеря информативности при переходе от 7 СЧ к 2 СЧ составляет около 19%, но зато появляется возможность визуализации многомерных исходных данных.
4. Нажать кнопку Факторные координаты для получения таблицы координат исходных переменных в пространстве новых выделенных факторов (ГК) (рис.13).
Рис.13. Координаты исходных переменных в пространстве главных компонентов (факторов)
Эта таблица дает возможность интерпретации ГК в терминах корреляции: большее абсолютное значение координат (факторной нагрузки) исходного признака с каким-либо ГК (фактором) говорит о том, что переменная сильнее связана с этим фактором. Другими словами, чем больше величина координаты признака, тем лучше переменные показывают структуру, представленную этим фактором.
Далее нажать на вкладке Переменные кнопку 2М график для построения соответствующего графика (рис.14).
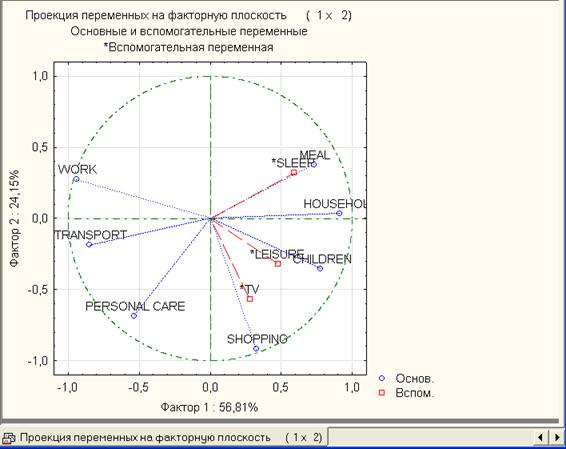
Рис.14. Переменные (признаки) в плоскости первых двух факторов (главных компонентов)
Как видно из рис.14, все переменные изображены в виде точек на единичном круге, так как корреляции (координаты точек) наблюдений с факторными осями принимают значения (по модулю) из интервала [0,1].
Горизонтальная ось соответствует фактору 1, вертикальная - фактору 2. Координаты точек - в таблице рис.12. Кроме того, этот рисунок дает возможность оценить корреляцию между признаками: чем меньше угол между радиус-векторами определенных признаков, тем сильнее корреляция между ними. Например, переменные work и transport находятся достаточно близко между собой, что свидетельствует об их сильной корреляции. Этот же вывод следует и из матрицы признак-признак.
5. На вкладке Наблюдения нажать кнопку 2М графики факторных наблюдений. Появится график (рис.15), на котором изображены все наблюдения (строки), использованные при расчете. При этом основные наблюдения (female) указаны кружочками синего цвета, а вспомогательные (male) отмаркированы квадратиками красного цвета. Из графика видно, что основные и вспомогательные наблюдения сгруппированы в разных областях плоскости, т.е. они объединены в разные кластеры.
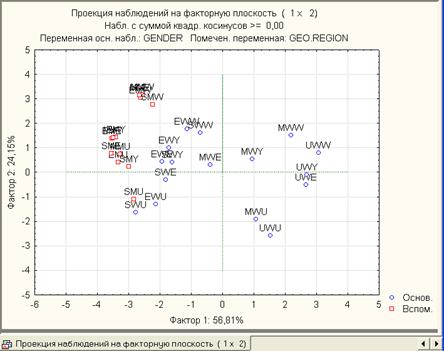
Рис.15. Наблюдения (строки) в плоскости первых двух факторов (главных компонентов)
3. Задание
В пакет Statistica ввести данные по результатам сессии 9 студенческих групп, сдавших по 4 экзамена (табл.). Ввод данных осуществляется через Файл -Создать, где в появившемся окне указать число переменных, равное 4, а число строк - 9. В таблице приведены средние баллы экзаменов по каждой дисциплине (ОИ - отечественная история; ЭТ – экономическая теория; МА – математический анализ; ЛА – линейная алгебра) для каждой из 9 групп.
Таблица Средние баллы каждой группы по 4 дисциплинам
| Номер группы | Отечественная история | Экономическая теория | Математический анализ | Линейная алгебра |
| 4,59 | 4,77 | 4,82 | 4,59 | |
| 4,68 | 4,73 | 4,27 | 4,38 | |
| 4,52 | 4,29 | 3,95 | 3,95 | |
| 4,64 | 4,5 | 4,45 | 4,41 | |
| 4,32 | 4,09 | 4,14 | 4,23 | |
| 4,36 | 4,27 | 4,05 | 4,23 | |
| 4,05 | 4,05 | 3,62 | 4,0 | |
| 3,9 | 3,95 | 3,63 | 3,86 | |
| 3,76 | 3,33 | 3,48 |
Вычислить:
1. Корреляцию между дисциплинами (построить матрицу признак-признак).
2. Расстояние между группами (построить матрицу группа-группа).
3. Собственные числа и главные компоненты (ГК).
4. Качество представления при двух ГК.
Построить графики:
1. Дендрограмму студенческих групп.
2. Дисциплины в плоскости ГК.
3. Группы в плоскости ГК.
4. Дисциплины в плоскости ГК.
Вопросы к защите работы
1. Как рассчитываются матрицы «объект-объект», «признак-признак»?
2. Что определяет собой дендрограмма?
3. Какая из матриц представления данных используется при кластерном анализе?
4. Как вычисляются ГК?
5. Какова размерность ГК?
6. Как выбирается число ГК?
7. Можно ли оценить потери информации при переходе к ГК?