ТЕЧЕНИЕ ВОЗДУХА
Основные закономерности течения воздуха (газа) те же, что и для жидкостей. Имеют место:
- ламинарный и турбулентный режимы течения. Для их разграничения также используется критерий Рейнольдса;
- установившийся и неустановившийся характер течения.
Кроме этого, используются и все остальные кинематические и динамические характеристики потоков: средняя скорость, объемный расход, массовый расход, давление, скоростной напор, мощность потока.
Из-за малой вязкости воздуха и, как правило, больших скоростей, режим в большинстве слу-чаев турбулентный.
Расчет параметров движущегося воздуха выполняют с учетом термодинамического процесса, изменяющегосяот изотермиического (с учетом теплообмена при Т = const), до адиабатного (без учета теплообмена).
Политропный процесс (политропный показатель n = 1,3…1,35) является более общим, охва-тывает изотермический и адиабатный процессы.
При больших скоростях течения воздуха процесс сжатия на местных сопротивлениях счи-тается адиабатным с адиабатным показателем k = 1,4.
При малых скоростях воздуха и большой протяженности магистралей процесс рассматрива-ют как изотермический n = 1.
Весь диапазон реальных процессов описывается уравнениями этих состояний.
В основу расчетов течения воздуха положено уравнение Бернулли для идеального газа:
ρgz + р + ρv2/2 = const (полное давление). Слагаемые уравнения (н/м2) называют:
ρgz – весовое давление, p – статическое давление, ρv2/2 – скоростное или динамическое дав-ление.
Весовым давлением часто пренебрегают и уравнение Бернулли принимает следующий вид:
р + ρv2/2 = const = Р0.
Эту сумму называют полным давлением P0.
Идеальным называют состояние газа, когда можно пренебречь силами межмолекулярного взаимодействия. Такие условия создаются при давлении до 10 МПа (~ 100 кгс/см2).
Для описания этого состояния используют уравнение Менделеева-Клайперона:
р = ρRT, (1)
где р – давление газа (Па) при температуре в градусах Кельвина Т (ºК). При атмосферном давлении (101325 Па или 1 атм – физическая атмосфера) Т = 273 ºК, ρ – плотность газа (кг/м3).
R – универсальная газовая постоянная, различная для разных газов, но не зависящая от темпе-ратуры и давления. Для воздуха R = 287 Дж/(кг∙ºК).
В области давлений до 10 МПа применение уравнения р = ρRT в расчетах пневмосистем дает погрешность не более 2%.
В пневматике есть два принципиальных отличия от расчета гидросистем:
1. - используют массовый расход, так как объемный расход изменяется по мере сжатия воздуха, а массовый нет: Q ρ1 = Q ρ2.
2. - при сверхзвуковой скорости течения воздуха меняется характер зависимости расхода от перепада давлений на местных сопротивлениях, поэтому рассматривают подкритический и надкритический режимы течения.
Истечение воздуха из резервуара
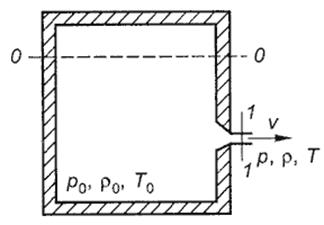Рассмотрим процесс истечения воздуха из резервуара через отверстие при поддержании в нем постоянного давления, рис. 1.
Рис. 1. Истечение газа из
отверстия в тонкой стенке
Размеры резервуара по сравнению с размерами выходного отверстия очень велики и можно пренеб-речь скоростью движения воздуха внутри резерву-ара. Следовательно, можно принять, что давление, температура и плотность воздуха внутри резервуара равны:
p 0 = Const, ρ0 = Const, T 0 = Const.
Из гидравлики известно, что скорость истечения жидкости определяется по формуле:
(1)
где μ – коэффициент расхода, Р 0 и Р – давления в резервуаре и за его пределами, ρ – плот-ность воздуха.
В отличие от жидкостей, газы сжимаются и при давлении до 10 МПа (~ 100 кгс/см2) их состо-яние описывается уравнением состояния идеального газа: р = ρRT, (2)
Термодинамический процесс при расширении воздуха близок к адиабатному и для него спра-ведливо соотношение:
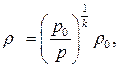(3)
где k – адиабатный показатель (для воздуха k ≈ 1,4), ρ и р – плотность и давление воздуха за пределами резервуара.
В формуле (1) разность давлений отнесена к плотности. Здесь пренебрегают тем, что плот-ность жидкости зависит от давления. Действительно, эта зависимость слишком слабая.
Для воздуха при разных давлениях разная плотность, поэтому формула (1) имеет вид:
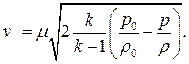(4)
При этом поправочный коэффициент, учитывающий сжимаемость воздуха определяется от-ношением: 
Учитывая, что для адиабатного процесса в соответствии с формулой (2) давление р 0 равна:
р 0 = ρ 0 RT 0, (5)
то после подстановки в выражение (4) формул (3) и (5) получим:
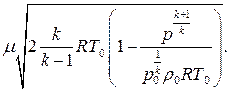(6)
В скобке плотность ρ 0 сокращается, RТ 0 выносим за скобку, но RТ 0 появляется в знаменателе второго члена в скобке, а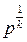 
из знаменателя уходит в числитель.
Делаем подстановку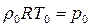 
, тогда в знаменателе второго члена получим: 
Выносим из под корня kRТ 0 и умножаем на f 0 (площадь отверстия), получаем зависимость объемного расхода от отношения давлений вне и внутри резервуара:
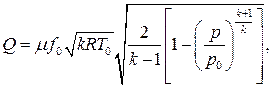
Массовый расход равен: Qρ = ρ Q,
поэтому окончательно выражение (6) примет вид:
(7)
где 
– скорость распространения звука в воздухе.
Размерность выражения для скорости звука: (Дж/кг ºК)· ºК.
Градусы Кельвина сокращаются, поэтому: н·м/кг → (кг·м/с2)·м /кг → м2/с2 → v зв (м/с).
Размерность формулы (7): м 2 
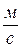→ кг/с это размерность массового расхода.
Формула (7) – это парабола со степенью 1/2. Если построить график зависимости массового расхода от отношения давлений p/p 0, то он будет иметь вид, показанный на рис. 2.
Отношение p/p 0 называется степенью расширения воздуха.
Анализ формулы (7) показывает, что выражение в квадратных скобках, обращается в ноль при p/ p 0 = 1. При этом расход воздуха равен нулю.
Рис. 2.
Зависимость массового расхода
газа от отношения давлений
Из графика видно, что при p/p 0 = 0,5 выражение (7) дает максимальное значение массового расхода Q ρmax.
(Критическое отношение (p/p 0)кр = 0,53, так как парабола немного несиммет-рична).
При p/p 0 < 0,5 имеет место так называемый надкритический режим. Расход воздуха должен уменьшаться в соответствии с пунктирной линией и при p/p 0 = 0 стать равным нулю, но этого не происходит, так как равенство p/p 0 = 0 соответствует истечению воздуха в вакуум. Но вакуума на Земле нет и поэтому расход также будет наибольшим и равным Q ρmax.
Таким образом, левая ветвь параболы фактически не реализуется.
Опыт показывает, что при постоянных ρ 0, T 0 и р 0 расход остается постоянным и равным мак-симальному (горизонтальная линия), а скорость истечения достигает критического значения, равного скорости звука: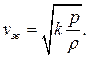 
(9)
Из выражения р = ρRT можно получить: RT = р / ρ и подставить в формулу: 
.
Тогда получим формулу (9).
Если скорость на выходе равна скорости звука v зв, любое дальнейшее увеличение давления внутри резервуара p 0 не увеличит скорость истечения, так как внутренний объем «заперт» потоком воздуха, выходящем со звуковой скоростью.
Тем не менее, в соответствии с формулой (7) увеличение р 0 будет приводить к увеличению плотности ρ 0, стоящему перед корнем, поэтому расход все же будет немного увеличиваться.
Таким образом, существует два режима истечения:
подкритический, при котором: p/p 0 < 0,53 (на рис. 2 справа);
и надкритический, при котором: p/p 0 > 0,53 (на рис. 2 слева);
При определении расходов воздуха предварительно по отношению давлений находят зону ис-течения (надкритический или подкритический режим), а затем рассчитывают расход.
Потери на трение воздуха учитывают коэффициентом расхода μ, который можно вычислить по формулам для истекающей жидкости, известной из курса общей гидравлики.