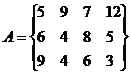Методические указания к выполнению задания
Постановка задачи.
Пусть имеется два игрока, один из которых может выбрать i-ю стратегию из m-возможных (i = 1,m), а второй, не зная выбора первого, выбирает j-ю стратегию из n-возможных (j = 1,n). В результате первый игрок выигрывает величину a(ij), а второй проигрывает эту величину.
Матрица

называется матрицей игры Строки матрицы А соответствуют стратегиям первого игрока, а столбцы - стратегиям второго. Эти стратегии называются чистыми
Число  называется нижней ценой игры, а соответствующая
называется нижней ценой игры, а соответствующая 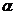 стратегия максимальной
стратегия максимальной
Число  называется верхней ценой игры, а соответствующая
называется верхней ценой игры, а соответствующая 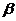 стратегия минимаксной.
стратегия минимаксной.
Нижняя цена игры всегда не превосходит верхнюю, т.е. 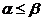 .
.
Решение игры не имеющей седловой точки.
Если  , то число V называется ценой игры, а сама игра есть игра с седловой точкой. Для игры с седловой точкой ее решение состоит в определении цены игры, а также минимаксной и максимальной стратегией игроков, которые и являются оптимальными. Т.о. решение в таком случае ищется в чистых стратегиях
, то число V называется ценой игры, а сама игра есть игра с седловой точкой. Для игры с седловой точкой ее решение состоит в определении цены игры, а также минимаксной и максимальной стратегией игроков, которые и являются оптимальными. Т.о. решение в таком случае ищется в чистых стратегиях
Решение игры, не имеющей седловой точки.
Если игра, заданная матрицей, не имеет седловой точки, то 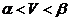 ,а для нахождения ее решения используют смешанные стратегии.
,а для нахождения ее решения используют смешанные стратегии.
Вектор, каждая из компонент которого показывает относительную частоту использования игроком соответствующей стратегии, называется смешанной стратегией данного игрока.
Обозначим:
 - смешанная стратегия первого игрока;
- смешанная стратегия первого игрока;

 - смешанная стратеги второго игрока.
- смешанная стратеги второго игрока.
Т.к.  и
и  - относительные частоты использования игроками чистых стратегий,
- относительные частоты использования игроками чистых стратегий,

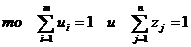
Если u* и z* - оптимальные смешанные стратегии первого и второго игроков, то цена игры вычисляется по формуле:
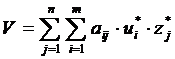
Определение оптимальных смешанных стратегий V*; Z* и цены игры и составляет процесс решения игры без седловой точки.
Теорема 1. Если один из игроков применяет оптимальную смешанную стратегию, то его выигрыш равен цене игры V. Вне зависимости от того, с какими частотами будет применять второй игрок стратегии, вошедшие в оптимальную, (в том числе и чистые стратегии).
С помощью теоремы 1 можно найти решение игр без седловой точки, размером 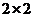 ;
; 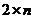 ;
;  .
.
4. Решение задач теории игр с помощью методов линейного программирования.
Теорема 2. Для того, чтобы число V было ценой игры а u* и z* - оптимальными стратегиями, необходимо и достаточно выполнение неравенств:
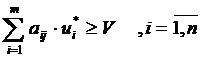 (1)
(1)
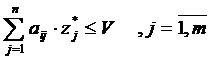 (2)
(2)
С помощью этой теоремы можно решить задачу теории игр любого размера 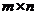 , предварительно преобразовав ее к задаче ЛП.
, предварительно преобразовав ее к задаче ЛП.
Рассмотрим игру 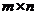 , определяемую матрицей:
, определяемую матрицей:
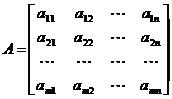
Разделим обе части неравенства (1) на V:
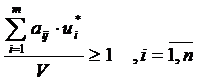
Обозначим u*i / V = y*i. Тогда:
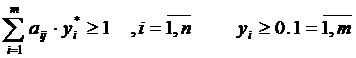
Используя введенное обозначение, перепишем условие 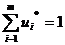 в виде
в виде 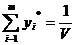 . Т.к. первый игрок стремится получить максимальный выигрыш, то он должен стремится обеспечить минимум величине
. Т.к. первый игрок стремится получить максимальный выигрыш, то он должен стремится обеспечить минимум величине  . Имеем задачу ЛП.
. Имеем задачу ЛП.
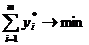 (3)
(3)
 (4)
(4)
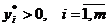 (5)
(5)
Рассуждая аналогично в отношении второго игрока, можно составить задачу, двойственную по отношению к (3), (4), (5)
 (6)
(6)
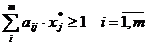 (7)
(7)
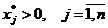 (8)
(8)
Используя решение пары двойственных задач, получаем выражение для определения стратегий и цены игры:
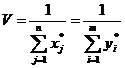 (9)
(9)
 (10)
(10)
Варианты заданий.
1. 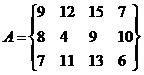 2.
2. 
3. 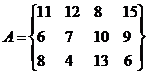 4.
4. 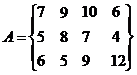
5. 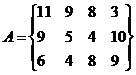 6.
6. 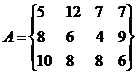
7. 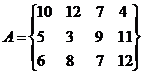 8.
8. 
9. 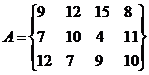 10.
10. 
11. 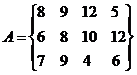 12.
12. 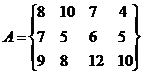
13. 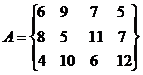 14.
14. 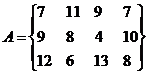
15.  16.
16.