Тема 1: Поведение функций на бесконечности. Асимптоты
Асимптота – это прямая, к которой график неограниченно приближается. Напомним, что асимптоты бывают горизонтальные, вертикальные и наклонные.


Например, у гиперболы вертикальной асимптотой является ось Ox, а вертикальной – Oy.

Пусть дана функция y = f(x), в области определения которой содержится луч от (a; + ∞) и пусть прямая y = b является горизонтальной асимптотой графика функции y = f(x). Тогда можно записать, что предел функции f(x) при x стремящемся к плюс бесконечности равен b.
Если же дана функция y = f(x), в области определения которой содержится луч (- ∞; a), и прямая y = b является горизонтальной асимптотой графика функции y = f(x), то можно записать, что предел функции f(x) при x стремящемся к минус бесконечности равен b.
Если одновременно выполняются оба соотношения, то можно записать, что предел функции f(x) при x стремящемся к плюс минус бесконечности равен b. Чаще всего знак плюс минус в данном равенстве убирают и просто говорят, что предел функции f(x) при x стремящемся к бесконечности равен b.

Пример1

Для вычисления предела функции на бесконечности используют несколько утверждений. Давайте сформулируем их.

Пример 2

Пример 3.

Пример 4

Тема 2: Понятие о производной функции, физический и геометрический смысл производной
Определение: Производной функции f(x) (f'(x0)) в точке x0 называется число, к которому стремится разностное отношение  , стремящемся к нулю.
, стремящемся к нулю.
Производные элементарных функций.

Правила дифференцирования.
Если у функций f(x) и g(x) существуют производные, то

Производная сложной функции:

Геометрический смысл производной.
Производная в точке x0 равна угловому коэффициенту касательной к графику функции y=f(x) в этой точке

Уравнение касательной к графику функции y=f(x) в точке x0: 
Физический смысл производной.
Если точка движется вдоль оси х и ее координата изменяется по закону x(t), то мгновенная скорость точки: 
Тема 3: Производные основных элементарных функций

Тема 4: Производные суммы, разности, произведения и частного





Тема 5:Производные сложной и обратной функций
Производная сложной функции
Пусть 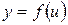 и
и  , тогда
, тогда  − сложная функция с промежуточным аргументом u и независимым аргументом х.
− сложная функция с промежуточным аргументом u и независимым аргументом х.
Теорема:
Если функции  имеет производную
имеет производную  в точке х, а функция
в точке х, а функция 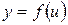 имеет производную
имеет производную  в соответствующей точке
в соответствующей точке  , то сложная функция
, то сложная функция  в точке х имеет производную
в точке х имеет производную  , которая находится по формуле:
, которая находится по формуле:  или
или  =
= 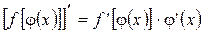
Кратко это можно сформулировать так (правило цепочки): производная сложной функции равна произведению производных от функций ее составляющих.
Данное правило распространяется на сложные функции при любом (определенном) числе промежуточных аргументов.
Так, если 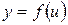 ,
,  ,
,  ,
,  , то
, то  .
.
Производная обратной функции
Если  и
и  − взаимо-обратные дифференцируемые функции и
− взаимо-обратные дифференцируемые функции и  , то
, то  или
или  , т.е. производная обратной функции равна обратной величине производной данной функции.
, т.е. производная обратной функции равна обратной величине производной данной функции.
Записывают:  или
или  .
.
Примеры:
1. Найти производную функции  .
.
Решение:  .
.
2. Найти производную функции  .
.
Решение:

3. Найти производную функции  .
.
Решение:



Подставим найденное в исходное: 
4. Найти производную функции 
Решение: 

5. Найти производную функции 
Решение:

6. Найти производную функции 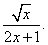
Решение:


7. Найти производную функции:  .
.
Решение:
