Составитель –И.Н. Курляндчик, преподаватель математики ГАПОУ МО «МонПК»
Краткая аннотация:
В данной работе представлены методические рекомендации, которые помогут обучающимися колледжа в усвоении предлагаемой учебной темы и выполнении практических работ по данной теме. Методическая разработка может быть использована в качестве дидактического материала на уроках при введении нового материала и на уроках обобщения и систематизации.
В методических рекомендациях сформулированы дидактические целиработ и цели развития, обучающегося при проведении этих работ:
Образовательная цель: способствовать формированию у обучающихся предметных компетенций
- выделить общие методы решения неравенств на примере решения иррациональных, показательных, логарифмических уравнений;
- способствовать дальнейшему закреплению навыка обучающихся в решении неравенств, использования различных языков математики (словесного, символического, графического).
Развивающая цель: способствовать развитию у обучающихся метапредметных компетенций:
- коммуникативных – формирование мыслительной, речевой деятельности, навыка сотрудничества;
- регулятивных – умение управлять собственной деятельностью.
Воспитательная цель: способствовать формированию у обучающихся личностных компетенций:
- смыслообразование – умение субъектного целеполагания (постановка учебных целей самим учеником, сознательно принимает решение);
- самоопределение – самооценка (оценка результатов собственной деятельности на уроке).
| Методы решений уравнений. | ||||||
| Примеры. | Метод разложение на множители. | Образец решения. | ||||
1. 
|
| Решить уравнение:
1.Определим общий множитель – это переменная 
2.Общий множитель вынесем за скобки 
3.Произведение равно нулю, если один из множителей равен нулю  
Ответ. 0; 2.
| ||||
2. 
|
| Решить уравнение:
1.Используем формулу a2-b2 = (a-b)(a+b)
2. Произведение равно нулю, если один из множителей равен нулю  
Ответ. 
| ||||
3. 
|
| Решить уравнение:
1.Группируем 
2. Вынести в каждой группе общий множитель в виде одночлена за скобки. 
3. Вынести в каждой новой группе общий множитель (в виде многочлена) за скобки 
4. Произведение равно нулю, если один из множителей равен нулю  
Ответ. 5: -b.
| ||||
| Метод разложение на множители | ||||||
| При решении тригонометрических уравнений, решаемых разложением на множители, можно использовать все известные способы разложения на множители: вынесение общего множителя за скобки, группировка, применение формул сокращённого умножения. | ||||||
| Тригонометрические уравнения | Тригонометрические уравнения | Тригонометрические уравнения | ||||
Решить уравнение: 
1.Определим общий множитель – это переменная 
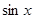2.Общий множитель вынесем за скобки 
3.Произведение равно нулю, если один из множителей равен нулю  
Ответ. 
| Пример. 1+ cosx +cos 2x =0.
Решение. Выражение 1+cos 2x заменяем выражением 2cos2 x. Тогда уравнение примет вид 2cos2 x+cosx=0
Разложив левую часть этого уравнения на множители: сosx (2cosx +1) =0, получаем:
сos x=0, x=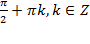 
2cos x +1 = 0, 2 cos x= -1, cos x =  -,
х=  arсcos  ,
x= 
Ответ: π/2+πk, k∈ Z, 2/3 π+2πn, n∈ Z.
| |||||
| Метод введения новой переменной. | ||||||
| Уравнения, представляющие собой квадратные уравнения относительно какой-либо тригонометрической функции, либо сводимые к нему. Если в уравнение входят тригонометрические функции, то их, если возможно, надо выразить через одну. При этом следует выбирать эту функцию так, чтобы получилось квадратное уравнение относительно неё уравнение. Введя вспомогательную переменную и решив квадратное уравнение, переходим к решению одного из простейших тригонометрических уравнений. | ||||||
Решить уравнение: 
Заменим  
Получим квадратное уравнение
Подставим в уравнение  значения 3 и 1
 б) 
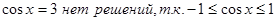Ответ: 
| ||||||
| I. Решение методами использования свойства ограниченности функции и использования равенства одноименных тригонометрических функций | |
1. Метод использования свойства ограниченности функций.
 
  
 
 
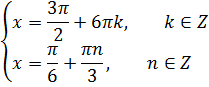
Ответ: 
| 1. Метод использования равенства одноименных тригонометрических функций.
 
 
Ответ: 
|
Однородные тригонометрические уравнения.
| Однородные тригонометрические уравнения первой степени | Однородные тригонометрические уравнения второй степени |
| A sin x+ B cos x = 0. Разделив обе части уравнения на cos x ≠ 0, получим уравнение вида tg x = С. Решаем простейшее уравнение вида tg x = С. | А sin2 х + В sinх cos х + С cos2х = 0 Разделив обе части уравнения на cos2 x ≠ 0, получим уравнение вида А tg 2x + В tg x + С = 0. |
| Пример. 2 sin x+ 3 cos x = 0. Решение. 2 sin x+ 3 cos x = 0 |: cos x ≠ 0 2 tg x + 3 =0 tg x = -1,5 х= arctg (-1,5) + πk, k Z или х = - arctg 1,5 + πk, k Z | Пример. 2 sin2 х - 3 sinх cos х - 5 cos2х =0 Решение. 2 sin2 х - 3 sinх cos х - 5 cos2х =0 2 sin2 х - 3 sinх cos х - 5 cos2х =0 |: cos2х ≠ 0 2 tg 2x - 3 tg x - 5 = 0 замена tg x = t, 2 t2 – 3 t – 5 =0, t1 = -1; t2 = 2,5 Решением уравнения tg х = -1 являются числа вида х = -π/4 + πk, k Z. Решением уравнение tg х = 2,5 являются числа вида х = arctg 2,5+ πn, n Z. |
При поиске плана решения более сложных тригонометрических уравнений можно воспользоваться таким ориентиром:
|