Определение момента инерции руки промышленного робота МРЛУ 901

Лабораторная работа №4

Цель работы: освоить методику экспериментального определения моментов инерции, масс и положения центров масс звеньев механизмов относительно их осей вращения.

 

Содержание

 

Ÿ Массы и моменты инерции звеньев

Ÿ Определение моментов инерции звеньев манипуляционных механизмов (описание лабораторной работы).

Ÿ ЗАДАНИЕ НА ВЫПОЛНЕНИЕ ЛАБОРАТОРНОЙ РАБОТЫ

Ÿ ВОПРОСЫДЛЯ КОНТРОЛЯ ЗНАНИЙ

 

1. Массы и моменты инерции звеньев

 

Массы и моменты инерции звеньев механизма определяют динамику механической системы. Их величины входят во многие формулы и уравнения, описывающие движение материальной системы или существующие закономерности в ней.

В механике, масса рассматривается как мера сопротивляемости тела изменению скорости, т.е. как «мера инертности». Согласно второму закону Ньютона, масса тела, совершающего прямолинейное движение, связана с действующей силой выражением 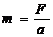(1):

, (1)

где m - масса тела в кг;

F - сила в Ньютонах (Н);

а - ускорение движения тела в м/с²

Во вращательном движении аналогичную роль выполняет момент инерции тела относительно его оси вращения. На основе равенства нулю алгебраической суммы моментов внешних сил (∑М_i) и сил инерции (J_oε) основного принципа кинетостатики, момент инерции вращающегося тела (J_о) относительно оси "О" может быть определен по формуле (2):

, (2)

где ε - угловое ускорение тела.

Момент инерции тела можно определить не только относительно оси вращения, но и относительно любой другой оси, рассматривая ее как потенциальную ось вращения. В курсе теоретической механики приводятся формулы перехода от центральной оси к оси параллельной ей 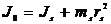(3).

, (3)

где J_s - момент инерции звена относительно оси вращения, проходящей через центр тяжести;

т_s - масса звена;

r_s - расстояние между осями.

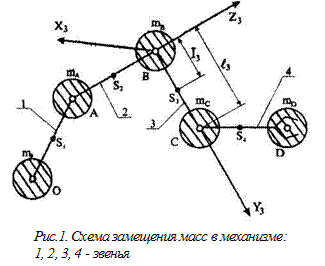
При кинетостатических исследованиях манипуляционных механизмов используется метод замещения масс - искусственный прием, облегчающий выполнение исследования. Масса i-го звена раскладывается на две составляющие массы (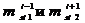), которые считаются приложенными в центрах его шарниров (рис.1). К ним добавляются массы () приводов перемещающих звенья манипуляционных механизмов. Заменяющие сосредоточенные массы (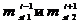) должны обладать свойствами общей массы (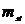), тем же положением центра масс и тем же моментом инерции (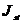). Как правило, начала применяемых систем координат (X,Y,Z) (рис.1) располагаются в ближайших к стойке шарнирах звена. Причем ось Y направляется вдоль оси звена. В связи с этим поставленные условия замещения масс будут выполнены в том случае, если [5]:

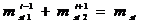(4)

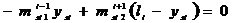(5)

;

;

;

;

;

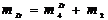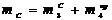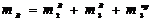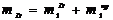где - масса привода, перемещающегося звена, расположенного после шарнира;

- масса объекта манипулирования;

длина звена;

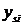- координата центра тяжести звена; i=2,3,4...;

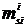- составляющая массы i -ого звена, отнесенная к центру одного из его шарниров.

Известными величинами принято считать m_si, l_i и y_si, а неизвестными- 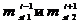. В общем случае момент инерции сосредоточенных масс (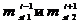) не равен моменту инерции (J_si) звена. Погрешность расчета составляет величину 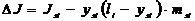(6),

(6)

что приведет к погрешности.определения момента (М_и) сил инерции, равной

ΔМ_и = ΔJε_si, (7)

где ε_si- угловое ускорение звена. При кинетостатических расчетах манипуляционных механизмов величиной ΔМ_и можно пренебречь.

Момент инерции звеньев, представляющих собой однородные тела и выполненные в виде простых геометрических тел (цилиндры, диски, призмы и т.д.), вычисляются по формулам, известным из курса теоретической механики. Моменты инерции звеньев действующих манипуляционных механизмов, представляющих собой тела сложной геометрической формы, определяются экспериментальными методами, с которыми студенты знакомы из курса механизмов и машин.

 

2. Определение моментов инерции звеньев манипуляционных механизмов (описание лабораторной работы)

Задачи и методы исследования. Определение моментов инерции, масс и положения центров масс звеньев манипуляционных механизмов при стендовых исследованиях промышленных роботов, составление уравнений равновесия моментов относительно оси вращения, изучение способов измерения и обработки результатов, измерение физических величин при экспериментальных исследованиях, освоение практических навыков по использованию лабораторного оборудования и экспериментальному исследованию механизмов и машин. При решении поставленных задач используется кинетостатический метод исследования, позволяющий выполнить их с использованием уравнений статики, присоединяя силы инерции к силам, действующим на материальную систему.

Описание работы. Одним из наиболее простых методов определения моментов инерции звеньев механизма относительно их осей вращения является метод разгона, известный из курсов теории механизмов и машин. Этот метод удобен, потому что им можно пользоваться при определении моментов инерции вращающегося звена, не вынимая его из механизма или машины. Для этого звено освобождается от силового замыкания и отсоединяется от последующих подвижных звеньев, установленных в кинематической цепи механизма, а его ось жестко связывается со шкивом, служащим для наматывания нити. В большинстве случаев на самом исследуемом звене можно отыскать цилиндрический поясок, удобный для наматывания нити. На рис.2, представлена схема измерения момента инерции звена у исследуемого механизма. Здесь звено 2 может свободно вращаться относительно оси О, закрепленной на неподвижном звене или стойке 6.

Со звеном 1 соосно и жестко связан шкив 2 радиуса r_о, на котором намотана нить 3 и закреплен один из ее концов. Далее нить 3 перекинута через шкив 4 и несет груз 5, привязанный к ее другому концу.

Если звено 1 повернуть так, чтобы груз 5 поднялся на высоту S_А, a потом систему, состоящую из звена 1, шкива 2 и 4, груза 5, связанную нитью 3, предоставить самой себе, то эта система под действием веса груза 5 придет в движение. Груз 5 будет опускаться, а нить 3, сматываясь со шкива 2, заставит его вращаться вместе со звеном 1.

При проведении эксперимента измеряется время (t) опускания груза 5 массой m_G на заданную высоту S_A. Величина: S_A- высота опускания груза, m_G - масса груза и r_о - радиус шкива считаются заданными. На основе этих данных составляется уравнение движения в виде (8)

J_∑0∙ε = r_o∙m_G(q - a) - M_{f (8)}

где J_∑0 - суммарный момент инерции звена 1 и шкива 2 относительно оси О;

ε_o - угловое ускорение звена 1;

q - ускорение свободного падения;

а - ускорение падения груза, определяемое по формуле:

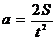, (9)

M_f - момент трения в опоре О.

В выражение (8) входит неизвестная величина момента трения M_f в опоре O звена 1. Для ее исключения используется относительный метод измерения. Для этого проводят две серии измерения (t) при падении грузов m₁ и m₂, подвешивая их поочередно на нить. Величины J_∑0 и r_о не изменяются. Величина момента трения M_f в опоре О при замене одного груза другим, изменение скорости падения груза и натяжение нити колеблется незначительно. Все это позволяет считать, что в обеих сериях измерения моменты трения одинаковы, т.е.

M_f1 ≈ M_f2. (10)

Учитывая, что

а = ε_о∙r_о (11)

для каждой серии измерения можно записать соответствующие уравнения движения (5.8)

J_∑0∙a₁ = r_o²∙m₁(q – a₁) - M_f∙ r_о, (12)

J_∑0∙a₂ = r_o²∙m₂ (q - a₂) - M_f∙ r_о. (13)

При вычитании из уравнения (12) уравнения (13) определяется выражение для вычисления J_∑0:

J_∑0= (14)

Величина J_∑0 включает в себя момент инерции J_1О звена 1 и момент инерции J_2О шкива 3, то есть:

J_∑0= J_1О + J_2О (15)

Следовательно, для определения J_1О из величины J_∑0 необходимо, исключить J_2О:

J_1О = J_∑0 - J_2О (16)

Добавочный момент инерции J_2О может быть вычислен по формулам, известным из курса теоретической механики. Используемые шкивы, как правило, изготавливаются в виде круглых цилиндров. Их момент инерции относительно оси вращения определяется по формуле

J_2О = 0,5∙m₂∙r₀² (17)

где m₂ - масса шкива.

Следует отметить, изложенный метод определения моментов инерции вращающихся звеньев механизма уменьшает погрешности измерения, возникающие вследствие того, что не учитывается момент инерции шкива 4 и момент трения в его опоре.

Зная суммарный момент инерции J_∑0 (14) можно определить момент трения в опоре О оси вращения звена 1. Для этого необходимо воспользоваться выражением (12).

На рис.3 представлена схема измерения моментов инерции звеньев манипуляционного механизма промышленного робота МРЛУ901, который используется для обслуживания металлорежущих станков, штамповочных прессов и в сборочных работах. Представленная схема измерения позволяет определить не только суммарный момент инерции колонны 1 и руки 2 с схватом относительно оси вращения колонны, но и массу, а также координату центра тяжести руки с схватом.. Порядок проведения операций измерения и расчетные формулы приведены выше. Время опускания груза 7 (m₇) на заданную высоту (S_А) измеряется механическим или электрическим секундомерами.

S_А = r_o∙φ

где φ - угол поворота колонны относительно вертикальной оси.

С этой целью на станине стенда установлены конечные выключатели 9 и 10 и электрический секундомер 11. Причем, в исходном положении, когда груз 7 поднят на заданную высоту, а нить намотана на шкив 5, нормально замкнутые контакты конечного выключателя 9 разомкнуты. В этом случае электрическая цепь секундомера разомкнута и отсчет времени не производится. В начальный момент опускания груза 7 происходит переключение контактов у выключателя 9: включается его нормально замкнутые контакты, тем самым, замыкается электрическая цепь секундомера и начинается отсчет времени опускания груза 7. Он продолжается до момента, когда груз 7 выключит нормальнозамкнутые контакты у конечного выключателя 10. Электрическая цепь секундомера разрывается, тем самым, прекращается отсчет времени опускания груза 7 на заданную высоту, ограничиваемую нитью 8.

При проведении экспериментальных исследований неизвестными величинами считаются:

t - время опускания груза на заданную высоту;

J_О - суммарный момент инерции колонны 1 и руки с схватом 2 относительно оси вращения О; т₂ - масса руки с схватом;

С - расстояние от центра руки с схватом до его предельного упора 4,

а известными величинами:

J_5О - момент инерции шкива 5 относительно оси вращения О;

r_о- радиус шкива 5;

а - расстояние между упорами 3 и 4 перемещения руки;

b - длина направляющей 12;

x_i - задаваемое текущее перемещение руки с схватом;

h = а - b - предельное перемещение руки с схватом;

m₂ - масса объекта манипулирования;

m₇ - масса груза 7;

S_А - высота опускания груза 7.

Согласно уравнению (14), выражение для вычисления суммарного момента инерции звеньев 1 и 2 манипуляционного механизма на рис.3 по результатом проведения двух серий измерений (с грузами m₇₁ и m₇₂) в исходном положении руки с схватом, когда текущая координата его перемещения равна b/2, примет вид:

J_∑00= 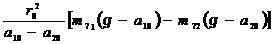(14)

 

где J_∑00 - суммарный момент инерции колонны 1, руки с схватом 2 и шкива 5 относительно оси вращения О в исходном положении руки, то есть когда x_i = b/2

J_∑00= J_О + J_5О (19)

J_О - суммарный момент инерции колонны 1 схвата 2 относительно оси вращения О:

J_О = J_1О + J_s2 + , (20)

где J_1О - момент инерции колонны 1 относительно оси вращения О;

J_s2 - момент инерции руки с схватом 2 относительно оси, проходящей через центр тяжести;

m₂ - масса руки с схватом;

J_5О - момент инерции шкива 5 относительно оси вращения О, определяемый по формуле (17);

С - координата центра масс руки с схватом в исходном положении.

Ускорения а₁₀ и а₂₀ опускания грузов m₇₁и m₇₂вычисляются по формуле (11).

Определив J_∑00и J_5О из выражения (19) вычисляется искомый суммарный момент инерции J_О подвижных звеньев манипуляционного механизма относительно оси вращения О для исходного положения руки (крайнее заднее положение).

Определение массы и центра масс руки с схватом выполняется в следующей последовательности. Максимальное перемещение схвата h = a - b делится на п отрезков (п ≥ 5). В соответствии с выполненным делением рука последовательно выдвигается на величину отрезка h/n. и в каждом положении, начиная с первого (при x₁ = b/2 +h/n) измеряется время опускания грузов m₇₁и m₇₂ на одну и ту же высоту S_A. Для каждого положения руки на основе уравнения (14) составляются выражения для вычисления суммарного момента инерции (J_∑0i) звеньев 1, 2 и шкива 5 относительно оси вращения O.

J_∑0i= (21)

 

где величина J_∑0i включает в себя:

J_∑0i = J_1О + J_s2 + J_5О + m₇ (x_i-c)2, (22)

где x_i - текущее перемещение руки с схватом.

Для исходного положения руки при x_i = b/2 необходимо использовать величину, определяемую выражениями (18), (19), (20).

Ускорение а_1i и a_2i опускания грузов m₇₁ и m₇₂ для каждого положения руки x_i = b/2 +i∙h/n определяется по формуле (11). По результатам вычислений (18) и (21) определяется разность

ΔJ_∑i= J_∑00 - J_∑0i =m₂ 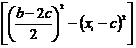. (23)

На основе выражения (23) строится график функции [ΔJ_∑i, x_i] (рис.4).График функции [ΔJ_∑i, x_i] позволяет определить координату С центра тяжести руки с схватом 2 (рис.2,3).

Зная координату центра тяжести руки с схватом, можно из выражения (23) определить массу схвата т₂ манипуляционного механизма:

. (24)

Это выражение упрощается, если выбрать x_i = c:

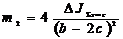. (25)

Координата центра масс (х_s2) руки с схватом, когда он выдвинут в крайнее переднее положение, определяется выражением:

x_s2 = a – c - .

Если воспользоваться уравнением (20), то можно вычислить суммарный момент инерции подвижных звеньев 1 и 2 манипуляционного механизма относительно их оси вращения О, когда схват выдвинут в крайнее переднее положение:

(26)

Момент трения M_f в опоре О определяется из выражения (12), когда известны все остальные величины, входящие в это уравнения.

Оборудование и инвентарь, используемые в лабораторной работе. Промышленный робот МРЛУ901, шкивы с нитью, набор грузов, линейка, секундомер, конечные выключатели.

Исходные данные. Масса объекта манипулирования m₂ = 0,2 кг. Масса грузов т₇₁ и т₇₂ выбирается по указанию преподавателя.

Измеряемые и расчетные величины. h - максимальное выдвижение схвата; Максимальное угловое перемещение руки φ; a - расстояние между упорами перемещения руки; b - длина направляющей; r₀ - радиус шкива; t -время опускания грузов т₇₁ и т₇₂; S_А - высота опускания грузов т₇₁ и т₇₂; J_5О - момент инерции шкива 5 относительно оси вращения; x_i - задаваемое текущее перемещение руки с схватом.

Результаты вычисления конечных величин.; J_О - суммарный момент инерции колонны и руки с схватом относительно оси вращения колонны в исходном положении схвата; m₂ - масса руки с схватом; С - координата центра тяжести руки с схватом в исходном положении; M_f - момент трения в опорах вращения колонны.

Заключение по работе. В заключении по работе необходимо указать методы исследования и измерения основных величин. Отчет по работе должен быть подписан студентом.

 

3. ЗАДАНИЕ НА ВЫПОЛНЕНИЕ ЛАБОРАТОРНОЙ РАБОТЫ

 

3.1. Изучить теоретические основы построения эксперимента для определения инерциальных характеристик тел

3.2. Изучить методику проведения эксперимента Выполнить движения по индивидуальному заданию.

3.3. Произвести измерения по предлагаемой методике.

3.4. Обработать результаты эксперимента.

7.5. Построить графики и определить инерциальные характеристики.

 

4. Вопросы для контроля знаний

 

4.1. Для чего производят измерения с двумя грузами различной массы?

4.2. Как определить положения центра масс по графику функции [ΔJ_∑i, x_i]?

4.3. С какой целью производится многократное измерение параметров в одном положении руки?

Список литературы:

 

1. Пономарев Б.Б. Основы конструирования и расчета исполнительных систем промышленных роботов. Учебное пособие. – Иркутск: Изд-во ИрГТУ, 2005. - 215 с.

2. Пономарев Б.Б. Основы конструирования и расчета несущих механических систем промышленных роботов. Учебное пособие. – Иркутск: Изд-во ИрГТУ, 2005. - 203 с.

3. Пономарев Б.Б.Механика автоматических устройств. Конспект лекций. ¾ Иркутск: ИрГТУ, 2008

4. Механика автоматических устройств. Методические указания по выполнению лабораторных работ. Составитель Пономарев Б.Б. ¾ Иркутск: ИрГТУ, 2008.

5. Основы робототехники: Учебное пособие для вузов/Н.В. Василенко, К.Д. Никитин, В.П. Пономарев, А.Ю. Смолин. Под. Ред. К.Д. Никитина. – Томск: МГП «РАСКО», 1993. 480 с.

6. Шахинпур М. Курс робототехники: Пер. с англ. – М.: Мир, 1990. – 527 с.

7. Красковский Е.Я., Дружинин D.A., Филатов Е.М. Расчет и конструирование механизмов приборов и вычислительных систем: Учебное по­собие для приборостроит. специальностей вузов. - М.:Высш.шк.,1991. - 480с.

8. Механика промышленных роботов: Учебн. пособие для втузов: В 3 кн./ Под ред. К.В. Фролова, Е.И. Воробьева. - М.: Высш.шк., 1988. – 376 с.

9. Филатова Л.С. Математическая обработка результатов измерений (конспект лекций). - Иркутск: ИрГТУ, 1997.