Перейдем теперь к оценке значимости коэффициентов регрессии  и построению доверительного интервала для параметров регрессионной модели
и построению доверительного интервала для параметров регрессионной модели  .
.
 ,
,
где  – несмещенная оценка параметра
– несмещенная оценка параметра  ;
;
 – диагональный элемент матрицы
– диагональный элемент матрицы  .
.
Среднее квадратическое отклонение (стандартная ошибка) коэффициента регрессии  примет вид:
примет вид:
 . (4.22)
. (4.22)
Значимость коэффициента регрессии 
 . (4.23)
. (4.23)
доверительный интервал для параметра 
 . (4.23')
. (4.23')
доверительный интервал для  :
:
 , (4.24)
, (4.24)
где  – групповая средняя, определяемая по уравнению регрессии,
– групповая средняя, определяемая по уравнению регрессии,
 (4.25)
(4.25)
– ее стандартная ошибка.
доверительный интервал для индивидуальных значений зависимой переменной  :
:
 , (4.26)
, (4.26)
где
 . (4.27)
. (4.27)
Доверительный интервал для параметра  с соответствующим изменением числа степеней свободы критерия
с соответствующим изменением числа степеней свободы критерия  :
:
 . (4.28)
. (4.28)
Пример 4.3. По данным примера 4.1 оценить сменную добычу угля на одного рабочего для шахт с мощностью пласта 8 м и уровнем механизации работ 6%; найти 95%-ные доверительные интервалы для индивидуального и среднего значений сменной добычи угля на 1 рабочего для таких же шахт. Проверить значимость коэффициентов регрессии и построить для них 95%-ные доверительные интервалы. Найти интервальную оценку для дисперсии  .
.
Решение. В примере 4.1 уравнение регрессии  .
.
надо оценить  , где
, где  .
.
Выборочной оценкой  является групповая средняя, которую найдем по уравнению регрессии:
является групповая средняя, которую найдем по уравнению регрессии:
 .
.
Для построения доверительного интервала для  необходимо знать дисперсию его оценки –
необходимо знать дисперсию его оценки –  . Для ее вычисления обратимся к табл. 4.2 (точнее к ее двум последним столбцам, при составлении которых учтено, что групповые средние определяются по полученному уравнению регрессии).
. Для ее вычисления обратимся к табл. 4.2 (точнее к ее двум последним столбцам, при составлении которых учтено, что групповые средние определяются по полученному уравнению регрессии).
Теперь по (4.21):  и
и  .
.
Определяем стандартную ошибку групповой средней  по формуле (4.25). Вначале найдем
по формуле (4.25). Вначале найдем

Теперь  .
.
По табл. II приложений при числе степеней свободы k =10–2–1=7 находим  . По (4.24) доверительный интервал для
. По (4.24) доверительный интервал для  равен
равен
 ,
,
или

Найдем доверительный интервал для индивидуального значения  при
при  :
:
по (4.27): 
и по (4.26):  ,
,
т. е.  .
.
Проверим значимость коэффициентов регрессии  и
и 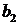 . В примере 4.1 получены
. В примере 4.1 получены 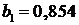 и
и  . Стандартная ошибка
. Стандартная ошибка  в соответствии с (4.22) равна
в соответствии с (4.22) равна
 .
.
Так как  , то коэффициент
, то коэффициент  значим. Аналогично вычисляем
значим. Аналогично вычисляем  и
и  т.е. коэффициент
т.е. коэффициент 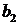 незначим на 5%-ном уровне.
незначим на 5%-ном уровне.
Доверительный интервал имеет смысл построить только для значимого коэффициента регрессии  : по (4.23'):
: по (4.23'):
 , или
, или  .
.
Найдем 95%-ный доверительный интервал для параметра  . Учитывая, что
. Учитывая, что  , найдем по таблице III приложений n – p –1= n –2–1= n –3 степенях свободы
, найдем по таблице III приложений n – p –1= n –2–1= n –3 степенях свободы
 ;
;
 .
.
По формуле (4.28)  ,
,
или  и
и  .
.
4.6. Оценка значимости множественной регрессии.
Коэффициенты детерминации  и
и 
Как и в случае парной регрессионной модели (см § 3.6), в модели множественной регрессии общая вариация Q – сумма квадратов отклонений зависимой переменной от средней (3.41) может быть разложена на две составляющие:
 ,
,
где  ,
,  – соответственно сумма квадратов отклонений, обусловленная регрессией, и остаточная сумма квадратов, характеризующая влияние неучтенных факторов.
– соответственно сумма квадратов отклонений, обусловленная регрессией, и остаточная сумма квадратов, характеризующая влияние неучтенных факторов.
Получим более удобные, чем (3.40), формулы для сумм квадратов Q,  и
и  , не требующие вычисления значений
, не требующие вычисления значений  , обусловленных регрессией, и остатков
, обусловленных регрессией, и остатков 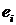 .
.
В соответствии с (3.40), (3.42)
 (4.29)
(4.29)
(ибо  ).
).
С учетом (4.4) имеем
 (4.30)
(4.30)
(ибо в силу (4.5)  ).
).
Наконец,
 . (4.31)
. (4.31)
Уравнение множественной регрессии значимо (иначе – гипотеза  о равенстве нулю параметров регрессионной модели, т. е.
о равенстве нулю параметров регрессионной модели, т. е.  , отвергается), если (учитывая (3.43)
, отвергается), если (учитывая (3.43)
при m=p +1)
 , (4.32)
, (4.32)
где  – табличное значение F -критерия Фишера–Снедекора, а
– табличное значение F -критерия Фишера–Снедекора, а  и
и  определяются по формулам (4.31) и (4.30).
определяются по формулам (4.31) и (4.30).
В § 3.6 был введен коэффициент детерминации  как одна из наиболее эффективных оценок адекватности регрессионной модели, мера качества уравнения регрессии, характеристика его прогностической силы.
как одна из наиболее эффективных оценок адекватности регрессионной модели, мера качества уравнения регрессии, характеристика его прогностической силы.
Коэффициент детерминации (или множественный коэффициент детерминации)  определяется по формуле (3.47) или с учетом (4.31), (4.29):
определяется по формуле (3.47) или с учетом (4.31), (4.29):
 . (4.33)
. (4.33)
Отметим еще одну формулу для коэффициента детерминации:
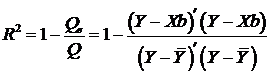 , (4.33')
, (4.33')
или 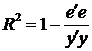 , (4.33")
, (4.33")
где  ,
, 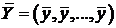 ,
,  – n-мерные векторы;
– n-мерные векторы;
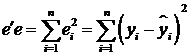 ,
,
 .
.
Напомним, что  характеризует долю вариации зависимой переменной, обусловленной регрессией или изменчивостью объясняющих переменных; чем ближе
характеризует долю вариации зависимой переменной, обусловленной регрессией или изменчивостью объясняющих переменных; чем ближе  к единице, тем лучше регрессия описывает зависимость между объясняющими и зависимой переменными.
к единице, тем лучше регрессия описывает зависимость между объясняющими и зависимой переменными.
Вместе с тем использование только одного коэффициента детерминации  для выбора наилучшего уравнения регрессии может оказаться недостаточным. На практике встречаются случаи, когда плохо определенная модель регрессии может дать сравнительно высокий коэффициент
для выбора наилучшего уравнения регрессии может оказаться недостаточным. На практике встречаются случаи, когда плохо определенная модель регрессии может дать сравнительно высокий коэффициент  .
.
Недостатком коэффициента детерминации  является то, что он, вообще говоря, увеличивается при добавлении новых объясняющих переменных, хотя это и не обязательно означает улучшение качества регрессионной модели. В этом смысле предпочтительнее использовать скорректированный (адаптированный, поправленный (adjusted)) коэффициент детерминации
является то, что он, вообще говоря, увеличивается при добавлении новых объясняющих переменных, хотя это и не обязательно означает улучшение качества регрессионной модели. В этом смысле предпочтительнее использовать скорректированный (адаптированный, поправленный (adjusted)) коэффициент детерминации  , определяемый по формуле
, определяемый по формуле
 , (4.34)
, (4.34)
или с учетом (4.33")
 . (4.34')
. (4.34')
Из (4.34) следует, что чем больше число объясняющих переменных р, тем меньше  по сравнению с
по сравнению с  . В отличие от
. В отличие от  скорректированный коэффициент
скорректированный коэффициент  может уменьшаться при введении в модель новых объясняющих переменных, не оказывающих существенного влияния на зависимую переменную. Однако даже увеличение скорректированного коэффициента детерминации
может уменьшаться при введении в модель новых объясняющих переменных, не оказывающих существенного влияния на зависимую переменную. Однако даже увеличение скорректированного коэффициента детерминации  при введении в модель новой объясняющей переменной не всегда означает, что ее коэффициент регрессии значим (это происходит, как можно показать, только в случае, если соответствующее значение t -статистики больше единицы (по абсолютной величине), т. е. | t |>1. Другими словами, увеличение
при введении в модель новой объясняющей переменной не всегда означает, что ее коэффициент регрессии значим (это происходит, как можно показать, только в случае, если соответствующее значение t -статистики больше единицы (по абсолютной величине), т. е. | t |>1. Другими словами, увеличение  еще не означает улучшения качества регрессионной модели.
еще не означает улучшения качества регрессионной модели.
Если известен коэффициент детерминации  , то критерий значимости (4.32) уравнения регрессии может быть записан в виде:
, то критерий значимости (4.32) уравнения регрессии может быть записан в виде:
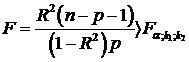 , (4.35)
, (4.35)
где  ,
,  , ибо в уравнении множественной регрессии вместе со свободным членом оценивается m = р +1 параметров.
, ибо в уравнении множественной регрессии вместе со свободным членом оценивается m = р +1 параметров.
Пример 4.4. По данным примера 4.1 определить множественный коэффициент детерминации и проверить значимость полученного уравнения регрессии Y по  и
и  на уровне α= 0,05.
на уровне α= 0,05.
Решение. Вычислим произведения векторов (см. пример 4.1):

и  (см. итоговую строку табл. 4.2). Из табл. 4.2 находим также
(см. итоговую строку табл. 4.2). Из табл. 4.2 находим также  , откуда
, откуда  .
.
Теперь по (4.33) множественный коэффициент детерминации
 .
.
Коэффициент детерминации  свидетельствует о том, что вариация исследуемой зависимой переменной Y – сменной добычи угля на одного рабочего на 81,1% объясняется изменчивостью включенных в модель объясняющих переменных – мощности пласта
свидетельствует о том, что вариация исследуемой зависимой переменной Y – сменной добычи угля на одного рабочего на 81,1% объясняется изменчивостью включенных в модель объясняющих переменных – мощности пласта  и уровня механизации работ
и уровня механизации работ  .
.
Проделав аналогичные расчеты по данным примера 3.1 для одной объясняющей переменной  , можно было получить
, можно было получить  (заметим, что в случае одной объясняющей переменной коэффициент детерминации
(заметим, что в случае одной объясняющей переменной коэффициент детерминации  равен квадрату парного коэффициента корреляции
равен квадрату парного коэффициента корреляции  ). Сравнивая значения
). Сравнивая значения  и
и  , можно сказать, что добавление второй объясняющей переменной
, можно сказать, что добавление второй объясняющей переменной  незначительно увеличило величину коэффициента детерминации, определяющего качество модели. И это понятно, так как выше, в примере 4.3, мы убедились в незначимости коэффициента регрессии
незначительно увеличило величину коэффициента детерминации, определяющего качество модели. И это понятно, так как выше, в примере 4.3, мы убедились в незначимости коэффициента регрессии 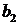 при переменной
при переменной  .
.
По формуле (4.34) вычислим скорректированный коэффициент детерминации:
при p =1  ;
;
при p =2  .
.
Видим, что хотя скорректированный коэффициент детерминации и увеличился при добавлении объясняющей переменной  , но это еще не говорит о значимости коэффициента
, но это еще не говорит о значимости коэффициента 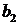 (значение t -статистики, равное 1,51 (см. § 4.4), хотя и больше 1, но недостаточно для соответствующего вывода на приемлемом уровне значимости).
(значение t -статистики, равное 1,51 (см. § 4.4), хотя и больше 1, но недостаточно для соответствующего вывода на приемлемом уровне значимости).
Зная  , проверим значимость уравнения регрессии. Фактическое значение критерия по (4.35):
, проверим значимость уравнения регрессии. Фактическое значение критерия по (4.35):

больше табличного  , определенного на уровне значимости α =0,05 при k 1=2 и k 2=10–2–1=7 степенях свободы (см. табл. IV приложений), т. е. уравнение регрессии значимо, следовательно, исследуемая зависимая переменная Y достаточно хорошо описывается включенными в регрессионную модель переменными Х1 и X2.
, определенного на уровне значимости α =0,05 при k 1=2 и k 2=10–2–1=7 степенях свободы (см. табл. IV приложений), т. е. уравнение регрессии значимо, следовательно, исследуемая зависимая переменная Y достаточно хорошо описывается включенными в регрессионную модель переменными Х1 и X2.
Упражнения
4.5. Имеются следующие данные о выработке литья на одного работающего Х 1(T), браке литья Х 2 (%) и себестоимости 1 т литья Y (руб.) по 25 литейным цехам заводов:
| i | x1j | x2j | yi | i | x1i | x2i | yi | i | x1i | x2i | yi |
| 14,6 | 4,2 | 25,3 | 0,9 | 17,0 | 9,3 | ||||||
| 13,5 | 6,7 | 56,0 | 1,3 | 33,1 | 3,3 | ||||||
| 21,5 | 5,5 | 40,2 | 1,8 | 30,1 | 3,5 | ||||||
| 17,4 | 7,7 | 40,6 | 3,3 | 65,2 | 1,0 | ||||||
| 44,8 | 1,2 | 75,8 | 3,4 | 22,6 | 5,2 | ||||||
| 111,9 | 2,2 | 27,6 | 1,1 | 33,4 | 2,3 | ||||||
| 20,1 | 8,4 | 88,4 | 0,1 | 19,7 | 2,7 | ||||||
| 28,1 | 1,4 | 16,6 | 4,1 | ||||||||
| 22,3 | 4,2 | 33,4 | 2,3 |
Необходимо: а) найти множественный коэффициент детерминации и пояснить его смысл; б) найти уравнение множественной регрессии Y по X1 и X2, оценить значимость этого уравнения и его коэффициентов на уровне α =0,05; в) сравнить раздельное влияние на зависимую переменную каждой из объясняющих переменных, используя стандартизованные коэффициенты регрессии и коэффициенты эластичности; г) найти 95%-ные доверительные интервалы для коэффициентов регрессии, а также для среднего и индивидуальных значений себестоимости 1 т литья в цехах, в которых выработка литья на одного работающего составляет 40 т, а брак литья – 5%.
4.6. Имеются следующие данные о годовых ставках месячных доходов по трем акциям за шестимесячный период:
| Акция | Доходы по месяцам, % | |||||
| А | 5,4 | 5,3 | 4,9 | 4,9 | 5,4 | 6,0 |
| В | 6,3 | 6,2 | 6,1 | 5,8 | 5,7 | 5,7 |
| С | 9,2 | 9,2 | 9,1 | 9,0 | 8,7 | 8,6 |
Есть основания предполагать, что доходы Y по акции С зависят от доходов Х 1 и Х 2 по акциям A и В. Необходимо: а) составить уравнение регрессии Y по X 1 и Х 2 ; б) найти множественный коэффициент детерминации R 2 и пояснить его смысл; в) проверить значимость полученного уравнения регрессии на уровне α =0,05; г) оценить средний доход по акции С, если доходы по акциям A и B составили соответственно 5,5 и 6,0%.
Глава 5
Некоторые вопросы практического использования регрессионных моделей
В предыдущих главах была изучена классическая линейная модель регрессии, приведена оценка параметров модели и проверка статистических гипотез о регрессии. Однако мы не касались некоторых проблем, связанных с практическим использованием модели множественной регрессии. К их числу относятся: мультиколлинеарность, ее причины и методы устранения; использование фиктивных переменных при включении в регрессионную модель качественных объясняющих переменных, линеаризация модели, вопросы частной корреляции между переменными. Изучению указанных проблем посвящена данная глава.
5.1. Мультиколлинеарность
Под мультикаллинеарностью понимается высокая взаимная коррелированность объясняющих переменных. Мультиколлинеарность может проявляться в функциональной (явной) и стохастической (скрытой) формах.
При функциональной форме мультиколлинеарности по крайней мере одна из парных связей между объясняющими переменными является линейной функциональной зависимостью. В этом случае матрица X'X особенная, так как содержит линейно зависимые векторы-столбцы и ее определитель равен нулю, т. е. нарушается предпосылка 6 регрессионного анализа. Это приводит к невозможности решения соответствующей системы нормальных уравнений и получения оценок параметров регрессионной модели.
Однако в экономических исследованиях мультиколлинеарность чаще проявляется в стохастической форме, когда между хотя бы двумя объясняющими переменными существует тесная корреляционная связь. Матрица XX в этом случае является неособенной, но ее определитель очень мал.
В то же время вектор оценок b и его ковариационная матрица  в соответствии с формулами (4.8) и (4.16) пропорциональны обратной матрице (X'Х)-1, а значит, их элементы обратно пропорциональны величине определителя | X'Х |. В результате получаются значительные средние квадратические отклонения (стандартные ошибки) коэффициентов регрессии b 0, b 1,..., bp и оценка их значимости по t -кpитepию не имеет смысла, хотя в целом регрессионная модель может оказаться значимой по F -критерию.
в соответствии с формулами (4.8) и (4.16) пропорциональны обратной матрице (X'Х)-1, а значит, их элементы обратно пропорциональны величине определителя | X'Х |. В результате получаются значительные средние квадратические отклонения (стандартные ошибки) коэффициентов регрессии b 0, b 1,..., bp и оценка их значимости по t -кpитepию не имеет смысла, хотя в целом регрессионная модель может оказаться значимой по F -критерию.
Оценки становятся очень чувствительными к незначительному изменению результатов наблюдений и объема выборки. Уравнения регрессии в этом случае, как правило, не имеют реального смысла, так как некоторые из его коэффициентов могут иметь неправильные с точки зрения экономической теории знаки и неоправданно большие значения.
Точных количественных критериев для определения наличия или отсутствия мультиколлинеарности не существует. Тем не менее имеются некоторые эвристические подходы по ее выявлению.
Один из таких подходов заключается в анализе корреляционной матрицы между объясняющими переменными Х1, Х2,..., Хp и выявлении пар переменных, имеющих высокие коэффициенты корреляции (обычно больше 0,8). Если такие переменные существуют, то говорят о мультиколлинеарности между ними.
Полезно также находить множественные коэффициенты детерминации между одной из объясняющих переменных и некоторой группой из них. Наличие высокого множественного коэффициента детерминации (обычно больше 0,6) свидетельствует о мультиколлинеарности.
Другой подход состоит в исследовании матрицы Х'Х. Если определитель матрицы X'X либо ее минимальное собственное значение λmin близки к нулю (например, одного порядка с накапливающимися ошибками вычислений), то это говорит о наличии мультиколлинеарности. О том же может свидетельствовать и значительное отклонение максимального собственного значения λmах матрицы Х'Х от ее минимального собственного значения λmin.
Для устранения или уменьшения мультиколлинеарности используется ряд методов. Самый простой из них (но далеко не всегда возможный) состоит в том, что из двух объясняющих переменных, имеющих высокий коэффициент корреляции (больше 0,8), одну переменную исключают из рассмотрения. При этом, какую переменную оставить, а какую удалить из анализа, решают в первую очередь на основании экономических соображений. Если с экономической точки зрения ни одной из переменных нельзя отдать предпочтение, то оставляют ту из двух переменных, которая имеет больший коэффициент корреляции с зависимой переменной.
Другой метод устранения или уменьшения мультиколлинеарности заключается в переходе от несмещенных оценок, определенных по методу наименьших квадратов, к смещенным оценкам, обладающим, однако, меньшим рассеянием относительно оцениваемого параметра, т. е. меньшим математическим ожиданием квадрата отклонения оценки b j от параметра βj или М (bj – βj)2.

Рис. 5.1
Оценки, определяемые вектором (4.8), обладают в соответствии с теоремой Гаусса—Маркова минимальными дисперсиями в классе всех линейных несмещенных оценок, но при наличии мультиколлинеарности эти дисперсии могут оказаться слишком большими, и обращение к соответствующим смещенным оценкам может повысить точность оценивания параметров регрессии. На рис. 5.1 показан случай, когда смещенная оценка  , выборочное распределение которой задается плотностью
, выборочное распределение которой задается плотностью  , «лучше» несмещенной оценки bj, распределение которой представляет плотность
, «лучше» несмещенной оценки bj, распределение которой представляет плотность  .
.
Действительно, пусть максимально допустимый по величине доверительный интервал для оцениваемого параметра βj есть  . Тогда доверительная вероятность, или надежность оценки, определяемая площадью под кривой распределения на интервале
. Тогда доверительная вероятность, или надежность оценки, определяемая площадью под кривой распределения на интервале  , как нетрудно видеть из рис. 5.1, будет в данном случае больше для оценки
, как нетрудно видеть из рис. 5.1, будет в данном случае больше для оценки  по сравнению с bj (на рис. 5.1 эти площади заштрихованы). Соответственно средний квадрат отклонения оценки от оцениваемого параметра будет меньше для смещенной оценки, т. е.
по сравнению с bj (на рис. 5.1 эти площади заштрихованы). Соответственно средний квадрат отклонения оценки от оцениваемого параметра будет меньше для смещенной оценки, т. е.

При использовании «ридж-регрессии» (или «гребневой регрессии») вместо несмещенных оценок (4.8) рассматривают смещенные оценки, задаваемые вектором  , где τ – некоторое положительное число, называемое «гребнем» или «хребтом», Ep+1 – единичная матрица (p +1)-го порядка. Добавление τ к диагональным элементам матрицы Х'Х делает оценки параметров модели смещенными, но при этом увеличивается определитель матрицы системы нормальных уравнений (4.5) – вместо (Х'Х) он будет равен | X'X+τEp+1 |.
, где τ – некоторое положительное число, называемое «гребнем» или «хребтом», Ep+1 – единичная матрица (p +1)-го порядка. Добавление τ к диагональным элементам матрицы Х'Х делает оценки параметров модели смещенными, но при этом увеличивается определитель матрицы системы нормальных уравнений (4.5) – вместо (Х'Х) он будет равен | X'X+τEp+1 |.
Таким образом, становится возможным исключение мультиколлинеарности в случае, когда определитель | Х'Х| близок к нулю.
Для устранения мультиколлинеарности может быть использован переход от исходных объясняющих переменных Х 1, X 2,..., Х n, связанных между собой достаточно тесной корреляционной зависимостью, к новым переменным, представляющим линейные комбинации исходных. При этом новые переменные должны быть слабокоррелированными либо вообще некоррелированными. В качестве таких переменных берут, например, так называемые главные компоненты вектора исходных объясняющих переменных, изучаемые в компонентном анализе, и рассматривают регрессию на главных компонентах, в которой последние выступают в качестве обобщенных объясняющих переменных, подлежащих в дальнейшем содержательной (экономической) интерпретации.
Ортогональность главных компонент предотвращает проявление эффекта мультиколлинеарности. Кроме того, применяемый метод позволяет ограничиться малым числом главных компонент при сравнительно большом количестве исходных объясняющих переменных.
5.2. Отбор наиболее существенных объясняющих переменных в регрессионной модели
Еще одним из возможных методов устранения или уменьшения мультиколлинеарности является использование пошаговых процедур отбора наиболее информативных переменных. Например, на первом шаге рассматривается лишь одна объясняющая переменная, имеющая с зависимой переменной Y наибольший коэффициент детерминации. На втором шаге включается в регрессию новая объясняющая переменная, которая вместе с первоначально отобранной образует пару объясняющих переменных, имеющую с Y наиболее высокий (скорректированный) коэффициент детерминации. На третьем шаге вводится в регрессию еще одна объясняющая переменная, которая вместе с двумя первоначально отобранными образует тройку объясняющих переменных, имеющую с Y наибольший (скорректированный) коэффициент детерминации, и т. д.
Процедура введения новых переменных продолжается до тех пор, пока будет увеличиваться соответствующий (скорректированный) коэффициент детерминации  (более точно – минимальное значение
(более точно – минимальное значение  ).
).
Пример 5.1. По данным n =20 сельскохозяйственных районов области исследуется зависимость переменной Y – урожайности зерновых культур (в ц/га) от ряда переменных – факторов сельскохозяйственного производства:
Х 1 – число тракторов (приведенной мощности на 100 га);
Х 2 – число зерноуборочных комбайнов на 100 га;
Х 3 – число орудий поверхностной обработки почвы на 100 га;
Х 4 – количество удобрений, расходуемых на 1 га (т/га);
X 5 – количество химических средств защиты растений, расходуемых на 1 га (ц/га).
Исходные данные1 приведены в табл. 5.1.
Таблица 5.1
| i (номер района) | yi | xi1 | xi2 | xi3 | xi4 | xi5 |
| 9,70 | 1,59 | 0,26 | 2,05 | 0,32 | 0,14 | |
| 8,40 | 0,34 | 0,28 | 0,46 | 0,59 | 0,66 | |
| ………………………………………………………………………………………….. | ||||||
| 13,10 | 0,08 | 0,25 | 0,03 | 0,73 | 0,20 | |
| 8,70 | 1,36 | 0,26 | 0,17 | 0,99 | 0,42 |
В случае обнаружения мультиколлинеарности принять меры по ее устранению (уменьшению), используя пошаговую процедуру отбора наиболее информативных переменных.
Решение. По формуле (4.8) найдем вектор оценок параметров регрессионной модели  , так что в соответствии с (4.9) выборочное уравнение множественной регрессии имеет вид:
, так что в соответствии с (4.9) выборочное уравнение множественной регрессии имеет вид:
 .
.
(5,41) (0,60) (21,59) (0,85) (1,54) (3,09)
В скобках указаны средние квадратические отклонения (стандартные ошибки)  коэффициентов регрессии bj, вычисленные по формуле (4.22). Сравнивая значения t -статистики (по абсолютной величине) каждого коэффициента регрессии βj по формуле
коэффициентов регрессии bj, вычисленные по формуле (4.22). Сравнивая значения t -статистики (по абсолютной величине) каждого коэффициента регрессии βj по формуле  , т.е.
, т.е.  с критическим значением
с критическим значением  , определенным по табл. II приложений на уровне значимости α=0,05 при числе степеней свободы k = n – p – 1 = 20 – 5 – 1 = 14, мы видим, что значимым оказался только коэффициент регрессии b 4 при переменной Х 4 – количество удобрений, расходуемых на гектар земли.
, определенным по табл. II приложений на уровне значимости α=0,05 при числе степеней свободы k = n – p – 1 = 20 – 5 – 1 = 14, мы видим, что значимым оказался только коэффициент регрессии b 4 при переменной Х 4 – количество удобрений, расходуемых на гектар земли.
Вычисленный по (4.33) множественный коэффициент детерминации урожайности зерновых культур Y по совокупности пяти факторов (X1 – X5) сельскохозяйственного производства оказался равным  , т. е. 51,7% вариации зависимой переменной объясняется включенными в модель пятью объясняющими переменными. Так как вычисленное по (4.35) фактическое значение F =3,00 больше табличного F 0,05;5;14=2,96, то уравнение регрессии значимо по F -критерию на уровне α=0,05.
, т. е. 51,7% вариации зависимой переменной объясняется включенными в модель пятью объясняющими переменными. Так как вычисленное по (4.35) фактическое значение F =3,00 больше табличного F 0,05;5;14=2,96, то уравнение регрессии значимо по F -критерию на уровне α=0,05.
По формуле (3.20) была рассчитана матрица парных коэффициентов корреляции:
| Переменные | Y | X1 | X2 | X3 | X4 | X5 |
| Y | 1,00 | 0,43 | 0,37 | 0,40 | 0,58* | 0,33 |
| X1 | 0,43 | 1,00 | 0,85* | 0,98* | 0,11 | 0,34 |
| X2 | 0,37 | 0,85* | 1,00 | 0,88* | 0,03 | 0,46* |
| X3 | 0,40 | 0,98* | 0,88* | 1,00 | 0,03 | 0,28 |
| X4 | 0,58* | 0,11 | 0,03 | 0,03 | 1,00 | 0,57* |
| X5 | 0,33 | 0,34 | 0,46* | 0,28 | 0,57* | 1,00 |
Знаком* отмечены коэффициенты корреляции, значимые по t -критерию (3.46) на 5%-ном уровне.
Анализируя матрицу парных коэффициентов корреляции, можно отметить тесную корреляционную связь между переменными Х1 и Х2 (r12 = 0,85), Х1 и Х3 (r13 = 0,98), X2 и Х3 (r23 = 0,88), что, очевидно, свидетельствует о мультиколлинеарности объясняющих переменных.
Для устранения мультиколлинеарности применим процедуру пошагового отбора наиболее информативных переменных.
1-й шаг. Из объясняющих переменных Х1–Х5 выделяется переменная X4, имеющая с зависимой переменной Y наибольший коэффициент детерминации  (равный для парной модели квадрату коэффициента корреляции
(равный для парной модели квадрату коэффициента корреляции  ). Очевидно, это переменная X4, так как коэффициент детерминации
). Очевидно, это переменная X4, так как коэффициент детерминации  – максимальный. С учетом поправки на несмещенность по формуле (4.34) скорректированный коэффициент детерминации
– максимальный. С учетом поправки на несмещенность по формуле (4.34) скорректированный коэффициент детерминации  .
.
2-й шаг. Среди всевозможных пар объясняющих переменных X4, Xj, j =1,2,3,5, выбирается пара (X4, Х3), имеющая с зависимой переменной Y наиболее высокий коэффициент детерминации  и с учетом поправки по (4.34)
и с учетом поправки по (4.34)  .
.
3-й шаг. Среди всевозможных троек объясняющих переменных (X4, Х3, Xj) j =1,2,5 наиболее информативной оказалась тройка (X4, Х3, X5), имеющая максимальный коэффициент детерминации  и соответственно скорректированный коэффициент
и соответственно скорректированный коэффициент  .
.
Так как скорректированный коэффициент детерминации на 3-м шаге не увеличился, то в регрессионной модели достаточно ограничиться лишь двумя отобранными ранее объясняющими переменными X4 и X3.
Рассчитанное по формулам (4.8), (4.9) уравнение регрессии по этим переменным примет вид:
 .
.
(0,66) (0,13) (1,07)
Нетрудно убедиться в том, что теперь все коэффициенты регрессии значимы, так как каждое из значений t -статистики
 ;
;  ;
; 
больше соответствующего табличного значения  .
.
Замечание. Так как значения коэффициентов корреляции весьма высокие (больше 0,8): r12 =0,85, r13 =0,98, r23 =0,88, то, очевидно, из соответствующих трех переменных X1, Х2, X3 две переменные можно было сразу исключить из регрессии и без проведения пошагового отбора, но какие именно переменные исключить – следовало решать, исходя из качественных соображений, основанных на знании предметной области (в данном случае влияния на урожайность факторов сельскохозяйственного производства).
Кроме рассмотренной выше пошаговой процедуры присоединения объясняющих переменных используются также пошаговые процедуры присоединения – удаления и процедура удаления объясняющих переменных, изложенные, например, в [1]. Следует отметить, что какая бы пошаговая процедура ни использовалась, она не гарантирует определения оптимального (в смысле получения максимального коэффициента детерминации  ) набора объясняющих переменных. Однако в большинстве случаев получаемые с помощью пошаговых процедур наборы переменных оказываются оптимальными или близкими к оптимальным.
) набора объясняющих переменных. Однако в большинстве случаев получаемые с помощью пошаговых процедур наборы переменных оказываются оптимальными или близкими к оптимальным.
5.3. Линейные регрессионные модели с переменной структурой. Фиктивные переменные
До сих пор мы рассматривали регрессионную модель, в которой в качестве объясняющих переменных (регрессоров) выступали количественные переменные (производительность труда, себестоимость продукции, доход и т. п.). Однако на практике достаточно часто возникает необходимость исследования влияния качественных признаков, имеющих два или несколько уровней (градаций). К числу таких признаков можно отнести: пол (мужской, женский), образование (начальное, среднее, высшее), фактор сезонности (зима, весна, лето, осень) и т. п.