Чем проще модель, тем реже она обманет
(Принцип надежности)
3.1 Математическая модель асинхронного двигателя в фазной заторможенной системе координат
Для решения задач анализа и синтеза электрических машин, при использовании теории цепей, создаются математические модели в различных координатных системах, каждая из которых имеет свою оптимальную область применения. При разработке программного комплексa макромоделирования асинхронных машин с учетом динамики была цспользована фазная заторможенная система кooрдинат. Модели в этой системе координат имеют неоспоримые преимущества по сравнению с моделями в ортогональных осях, когда требуется моделировать многоорбразие физических процессов в электрической машине. Кроме того, современная электрическая машина является, как правило, звеном болеее сложной цепи. Если внешняя цепь проста, то ее можно преобразовать к системе координат, в которой записаны уравнения машины, если сложна, то её преобразования очень громоздки. Такого рода задачи можно решать в фазных координатах, но здесь система дифференциальных уравнений содержит периодические коэффициенты, обусловленные вращением ротора машины, что увеличивает время численного решения. Задачи этого вида эффективно решаются с применением фазной заторможенной системы координат [6]. Фазы статора при этом преобразовании остаются без изменения, что позволяет пользоваться уравнениями электрического равновесия цепи статора в их исходной форме.
Математическая модель, предложенная Кроном, представляет собой “идеализированную” двухфазную симметричную электрическую машину с двумя обмотками на статоре и двумя обмотками на роторе по ортогональным осям. “Идеализированная” машина имеет гладкий воздушный зазор, без пазов на статоре и ротope, обмотки в виде токовых слоев, имеющих синусоидальное распределение магнитодвижущей силы. Машина ненасыщена, она не имеет нелинейных сопротивлений, поэтому при питании обмоток синусоидальным напряжением поле в воздушном зазоре синусоидальное. Для трехфазной "идеализированной" машины система дифференциальных уравнений в фазных осях имеет следующий вид:
dΨA/dt = - iARA + uA, (3.1)
dΨB/dt = - iBRB + uB, (3.2)ΨC/dt = - iCRC + uC, (3.3)Ψa/dt = - iaRa + ua, (3.4)Ψb/dt = - ibRb + ub, (3.5)Ψc/dt = - icRc + uc, (3.6)
dωr /dt = p0/J (MЭ - MC), (3.7)θ/dt = ωr, (3.8)
где Ψj - потокосцепления фаз; ij - токи в фазах; uj - питающие напряжения фаз; ωr - частота вращения ротора; р0 - число пар полюсов машины; J - момент инерции;
МЭ - электромагнитный момент; MС - момент сопротивления на валу; θ - угол поворота ротора.
На рис.3.1 показаны реальные: А, В, С, а, b, с и заторможенные: А, В, С, а~, b~, с~ координатные оси трехфазной системы. На основе проекций токов фаз ротора ia, ib, ic на оси фаз статора находятся выражения для преобразованных токов ротора ia~, ib~, ic~(то же самое для напряжений и потокосцеплений). При их использовании составляется матрица преобразования [9]:
__ 1
M3 = 2/3 cosθ 2/3 cos(θ+ρ) 2/3 cos(θ-ρ), (3.9)
2/3 cos(θ-ρ) 2/3 cosθ 2/3 cos(θ+ρ)
2/3 cos(θ+ρ) 2/3 cos(θ-ρ) 2/3 cosθ
где ρ=2π/3.
Система уравнений (3.1 - 3.8) переписывается в матричной форме
_ _ _
и = [R]∙i + dΨ/dt, (3.10)
_ _
здесь u = cо1оn(uА, uB, uC, ua, ub, uc), i = colon(iA, iB, iC, ia, ib, ic), [R] = diag(RA, RB, RC, Ra, Rl,, Rc), Ψ = cо1оn(ΨА, ΨB, ΨC, Ψa, Ψb, Ψc).

Рис.3.1. Реальные (А,В,С,а,b,с) и заторможенные (А,В,С,а~,b~,с~) трехфазные координаты
Умножив (3.10) на M3, имеем
M3 ∙ u =[R]∙ M3 ∙ i + M3 ∙ dΨ/dt, (3.11)∙ u = u.~, (3.12)∙ i = i.~, (3.13)
[R] = [R].~.
Принимаем
= Rb = Rc = Rr, ∙Ψ = Ψ.~. (3.14)
Одно из слагаемых выражения (3.11) имеет вид
d(M3∙Ψ)/dt = M3 ∙dΨ/dt + dM3/dt ∙Ψ,∙ dΨ/dt = dΨ.~/dt - dM3/dt ∙Ψ. (3.15)
В выражениях (3.12) - (3.15) u.~, i.~, Ψ.~ - преобразованные величины, которые равны
.~ = со1оп(uA, uB, uC, ua~, ub~, uc~),
i.~ = colon(iA, iB, iC, ia~, ib~, ic~),
Ψ.~ = colon(ΨA, ΨB, ΨC, Ψa~, Ψb~, Ψc~).
Определим выражение dM3/dt ∙Ψ.
__ 0
dM3 /dt = -2/3 dθ/dt sinθ sin (θ+ρ) sin (θ-ρ). (3.16)
sin (θ-ρ) sinθ sin (θ+ρ)(θ+ρ) sin (θ-ρ) sinθ
Выражение (3.16) умножается на матрицу столбец Ψ, после преобразований имеем
__ __ _ 0= dM3/dt ∙Ψ = ωr /√3 Ψc~ - Ψb~, (3.17)
Ψa~ - Ψc~
Ψb~ - Ψa~
Преобразованные дифференциальные уравнения в матричной форме имеют вид
.~ = [R].~ ∙ i.~+ dΨ.~/dt - G. (3.18)
Относительная частота вращения ротора имеет вид: v = ωr /ω, где ωr - частота вращения ротора; ω - частота вращения поля.
Итак, имеем систему дифференциальных уравнений электрического равновесия контуров статора и ротора в заторможенных трехфазных координатах
uA = RA ∙iA + dΨA/dt; (3.19)
uB = RB ∙iB + dΨB/dt; (3.29)
uC = RC ∙iC + dΨC /dt; (3.21)
ua~ = Ra~ ∙ia~ + dΨa~ /dt + (Ψb~ - Ψc~) ∙ vω/√3; (3.22)
ub~ = Rb~ ∙ib~ + dΨb~ /dt + (Ψc~ - Ψa~) ∙ vω/√3; (3.23)
uc~ = Rc~ ∙ic~ + dΨc~ /dt + (Ψa~ - Ψb~) ∙ vω/√3; (3.24)
Система дифференциальных уравнений (3.19) - (3.24), уравение движения, алгебраические уравнения электромагнитного момента и потокосцеплений представляют идеализированную математическую модель асинхронной машины в заторможенных координатах.
3.2 Особенности построения алгоритмов макромоделирования асинхронных двигателей с учетом динамики
Программный комплекс моделирования асинхронных машин с учетом динамики представлен макромоделью в фазной заторможенной системе координат, состоящей из одного контура на статоре и двух контуров на роторе, расположенных по одной оси. Комплекс позволяет учитывать многообразие физических процессов в асинхронной машине. Он построен по принципу многоуровневого моделирования и включает три модели:
Модель асинхронной машины с учетом насыщения по главному магнитному пути и путям потоков рассеяния, вытеснения тока в стержнях ротора, роторных вихревых токов (двухклеточный двигатель), динамических энергетических показателей, несинусоидальности напряжения питания (модель 1).
Модель с учетом насыщения по главному магнитному пути и путям потоков рассеяния, вытеснения тока в стержнях ротора, динамичеких энергетических показателей, несинусоидальности напряжения питания (модель 2).
Модель идеализированную (модель 3).
Уравнения электрического равновесия модели I, в матричной форме, имеют вид
dΨ.~/dt = - [R].~ ∙ i.~ + G + u.~ (3.25)
или дΨ.~/дi.~ ∙di.~/dt = - [R].~ ∙ i.~ + G.~ + u.~,
где Ψ.~ = colon(ΨA, ΨB, ΨC, Ψa1~, Ψb1~, Ψc1~, Ψa2~, Ψb2~, Ψc2~),.~ = colon(iA, iB, iC, ia1~, ib1~, ic1~, ia2~, ib2~, ic2~),.~ = со1оп(uA, uB, uC, ua1~, ub1~, uc1~, ua2~, ub2~, uc2~),
[R].~ = diag(RA, RB, RC, Ra1~(v), Rb1~(v), Rc1~(v), Ra2~, Rb2~, Rc2~),
G = vω/√3 colon(0, 0, 0, Ψc1~ - Ψb1~, Ψa1~ - Ψc1~, Ψb1~ - Ψa1~, Ψc2~ - Ψb2~, Ψa2~ - Ψc2~, Ψb2~ - Ψa2~).
Математическая модель асинхронной машины включает выражение для электромагнитного момента
Э = p0 √3/2 Lμ [(iA ic1~+ iB ia1~+ iC ib1~) - (iA ib1~+ iB ic1~+ iC ia1~) + (iA ic2~+ iB ia2~+ iC ib2~) - (iA ib2~+ iB ic2~+ iC ia2~)] (3.26)
и уравнения движения
/dt = p0 /Jω (MЭ - MC), (3.27)θ/dt = vω.
Для учета переменного насыщения магнитной системы асинхронного двигателя здесь применен метод статических и дифференциальных индуктивностей, преимущество которого заключается в едином подходе к учету насыщения главного магнитного пути и путей потоков рассеяния. Особенность этого метода состоит в составлении матрицы динамических параметров, в которую входят статические и дифференциальные индуктивности, зависящие от результирующих токов машины и частоты вращения ротора [7]. Статические и дифференциальные индуктивности определяются из экспериментальных или расчетных характеристик намагничивания. При использовании метода статических и дифференциальных индуктивностей необходимо определить первый член дифференциального уравнения дΨ.~/дi.~ - матрицу динамических параметров. Полная матрица динамических параметров учитывает уравнения электрического равновесия и уравнения движения. Элементы матрицы динамических параметров рассчитываются с применением матричного математического аппарата.
Индуктивности, входящие в матрицу динамических параметров, определяются зависимостями:
(iS) = ΨS (iS) / iS, Lr1S(ir1) = Ψr1 (ir1) / ir1, LμS(iμ) = Ψμ (iμ) / iμ, (3.28)
для статических индуктивностей и
(iS) = dΨS (iS) / diS, Lr1d(ir1) = dΨr1 (ir1) / dir1, Lμd(iμ) = dΨμ (iμ) / diμ, (3.29)
для дифференциальных индуктивностей.
Здесь LS - индуктивность рассеяния статорной обмотки; Lr1 - индуктивность рассеяния первого роторного контура; Lμ - взаимная индуктивность между обмотками статора и ротора.
Роторные вихревые токи учитываются в схеме замещения асинхронной машины вторым роторным контуром, расположенным по каждой оси (см. параграф 2.3). Это также может быть модель двухклеточного двигателя.
При разбеге двигателя из-за вытеснения тока в стержнях ротора меняется активное Rr1 и индуктивное Хr1 сопротивления первого роторного контура. Эффект вытеснения тока в стержнях ротора учитывается коррекцией активных и индуктивных сопротивлений основного роторного контура на каждом шаге интегрирования дифференциальных уравнений коэффициентами, рассчитанными при использовании метода разделения стержня на элементарные слои [8].
При известной конфигурации магнитных линий потока рассеяния в пазу стержень роторной обмотки представляется подразделенным на большое число элементарных слоев, изолированных друг от друга бесконечно тонким слоем изоляции. Границы слоев определяются магнитными силовыми линиями. Для каждого элементарного слоя находятся активное и индуктивное сопротивления в расчете на единицу длины стержня. При каждом значении скольжения определяются токи элементарных слоев, после чего рассчитываются активное и индуктивное сопротивления стержня с учетом вытеснения тока. Полученные значения коэффициентов вытеснения тока пересчитываются на величины полных активных и индуктивных сопротивлений первого роторного контура, после чего производится коррекция параметров основного роторного контура. Эти операции исполняются на каждом шаге интегрирования дифференциальных уравнений.
Итак, считается, что Rr1 и Lr1 = Хr1/ω постоянны и определены при коэффициентах вытеснения тока равных единице. Тогда истинные значения активного сопротивления и индуктивности первого роторного контура при каждом значении частоты вращения ротора выражаются следующими уравнениями:
(v) = Rr1∙KR(v); Lr1(v) = Lr1∙KX(v),
где KR(v) - коэффициент вытеснения тока активного сопротивления, KX(v) - коэффициент вытеснения тока индуктивного сопротивления.
Коэффициенты, учитывающие эффект вытеснения тока в стержнях ротора, рассчитываются по следующим выражениям:
KR(v) = (RCT ∙ K’R (v) + RЛ) / (RCT + RЛ);(v) = (λCT ∙ K’X (v) + λОСТ) / (λCT + λОСТ),
где RCT - активное сопротивление стержня; RЛ - активное сопротивление лобовых частей; K’R (v) - коэффициент вытеснения тока активного сопротивления, рассчитанный по [8], λCT - магнитная проводимость стержня; λОСT - сумма остальных магнитных проводимостей (дифференциальной, лобовых частей, скоса пазов); K’X (v) - коэффициент вытеснения тока индуктивного сопротивления, рассчитанный по [8].
Учет энергообмена в динамике реализуется в программном комплексе в соог ветствии с результатами исследований, изложенных в [9]. В динамике структура обменных процессов значительно усложняется, возникают новые малоизученные особенности и для адекватного описания процессов энергообмена в математической модели электрической машины с учетом динамики применяются "динамические" энергетические показатели с использованием значений токов и напряжений в данный момент времени.
Полная мощностьздесь определяется как максимально возможное значение активной мощности при заданных потерях, обусловленных токами, протекающими по обмоткам двигателя.
Выражение для определения мгновенного значения полной мощности имеет следующий вид:
m m(t) = [Σ uk2(t)∙ Σ ik2(t)]1/2,
k=1 k=1
где uk(t) и ik(t) - мгновенные значения напряжения и тока в фазе k; m - число фаз.
Расчет мгновенной активной мощности, потребляемой асинхронным двигателем, производится по выражению
M m(t) = Σ uk(t)∙ Σ ik(t).
k=1 k=1
Мгновеннaя механичecкaя мощность на валу двигателя имеет вид
(t) = ω(t)∙ MЭ(t),
где ω(t) и MЭ(t) - мгновенные значения угловой скорости вращения ротора и электромагнитного момента, развиваемого двигателем.
При моделировании используются интегральные и средние энергетические показатели. Интервалом усреднения в переходном процессе целесообразно принять период основной гармоники питающего напряжения T =2π/ω0 в установившемся режиме, где ω0 - частота основной гармоники напряжения в стационарном режиме.
Тогда интегральная полная мощность за период T имеет вид
t+T t+T m mП(t) =T -1 ∫s(t)dt = T -1 ∫ [Σ uk2(t)∙ Σ ik2(t)]1/2dt.
T t k=1 k=1
Интегральные значения за период активной и механических мощностей определяются выражениями:
t+T m t+T
pП(t) = T -1 ∫s(t)dt = ΣT -1 ∫ [uk(t) ∙ ik(t)] dt,
t t+T k=1 tП(t) = T -1 ∫[ω(t)∙MЭ(t)] dt,
t
Среднее значение коэффициента отношения активных мощностей за период имеет вид
ηП(t) = p2П(t) / pП(t).
3.3 Проблемно-ориентированный численный метод - основа реализации алгоритмов динамики асинхронной машины
Специфика математической модели электрической машины с характерной связью Ψ = fΨ (i), а не i = fi (Ψ) предопределяет выбор методов ее реализации. У аналитических методов построение математических моделей электрической машины в нормальной форме Коши связано с необходимостью аналитического решения характеристик намагничивания относительно токов или аналитического обращения матрицы динамических параметров, что возможно только для относительно несложных математических моделей.
У численных методов построение математических моделей электрической машины в нормальной форме Коши связано с необходимостью численного решения уравнений характеристик намагничивания или численным обращением матрицы динамических параметров на каждом шаге расчета, если характеристики намагничивания отражают нелинейную зависимость между потокосцеплением и током намагничивания.
Примененный в программном комплексе макромоделирования асинхронных машин алгоритм предназначен для исследования динамических режимов электрических машин при учете насыщения, вихревых токов и других физических явлений, делающих невозможной или трудно выполнимой операцию обращения матрицы динамических параметров, необходимую для перехода к уравнениям динамики в нормальной форме Коши [10].
Математическая модель представляет собой систему обыкновенных дифференциальных и алгебраических уравнений, записанных в канонической форме:
dΨ/dt = f(i,t),
Ψ = fΨ(i). (3.30)
Здесь Ψ, i - векторы, компонентами которых являются потокосцепления и токи контуров, дополненные механическими переменными - частотой вращения ω и углом поворота ротора θ. Первое уравнение из (3.30) включает в себя уравнения контуров, движения и связи между переменными ω и θ. Второе уравнение из (3.30) включает характеристики намагничивания машины и тождества для выравнивания размерности первого и второго уравнений. Перепишем (3.30) следующим образом:
dΨ/dt = dΨ/di ∙ di/dt = f(i,t); (3.31)
дfΨ(i)/дi ∙ di/dt = f(i,t). (3.32)
где дfΨ(i)/дi = L(i) - матрица динамических параметров.
Если приводить исходные уравнения (3.30) к нормальному виду Коши, следовало бы осуществить следующие преобразования:
dΨ/dt = f(i,t) → dΨ/dt = g(Ψ,t).
что либо сложно, либо для ряда моделей невозможно. Полагая матрицу динамических параметров L(i) - постоянной на каждом шаге расчета матрицы Якоби вектор-функции f(i,t) имеем
L(i)di/dt = f(i,t),
или di/dt = [L(i)]-1∙f(i,t) = F(i,t), (3.33)
что даcт возможность решения задачи численным методом.
Практическая задача, которая решается при построении канонических численных методов, заключается в таком выборе схемы правила, когда число наиболее сложных операций обращения матрицы динамических параметров сводится к минимально возможному.
Этой цели при сохранении порядка точности метода отвечает видоизмененная схема классического метода Рунге-Кутты [10]. Устойчивость метода дает возможность выбирать шаг интегрирования только из условия точности. Этим значительно расширяется класс решаемых динамических задач.
Программный комплекс моделирования динамических режимов асинхронных двигателей реализован в программной среде Microsoft Fortran Power Station. Построение графиков выполняется в программном пакете Grafer. B зависимости от сложности исследовательской задачи, согласно коду выбора модели, численные эксперименты выполняюся на моделях, учитывающих многообразие воздействующих факторов (модели 1,2) либо на идеализированной модели (модель З).
Алгоритм предусматривает возможность варьировать форму питающего напряжения. Напряжение может быть синусоидальным, синусоидальным с набором высших гармонических, прямоугольным, прямоугольно ступенчатым. Ввод исходных данных: параметров схемы замещения машины, момента инерции, величины фазного напряжения питания и т.д. доступен и удобен для решения различных исследовательских задач. Для учета насыщения, массивы значений статических и дифференциальных индуктивностей должны предварительно вычисляться. На рис.3.2-3.5 приводятся характеристики динамических режимов асинхронных двигателей средней мощности, полученные в результате численных экспериментов.

Рис.3.2. Пуск асинхронной машины, Р=ЗкВт, на холостом ходу (модель 3)



Рис.3.3. Пуск асинхронной машины, Р=11 кВт, на холостом ходу (модель1)

Рис.3.4. Пуск асинхронной машины, F=11 кВт, на холостом ходу (модель 1). Токи в фазах статора




Рис.3.5. Пуск асинхронной машины, Р=3 кВт, при моменте сопротивления 20 Нм (модель 2)

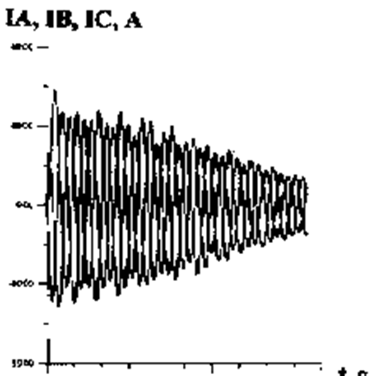




Рис.3.6. Пуск асинхронной машины, Р=3 кВт, при моменте сопротивления 20 Нм (модель 2). Токи в фазах статора
На основе программного комплекса моделирования асинхронных машин с учётом динамики решаются задачи статистического моделирования, с использованием метода планирования эксперимента, и оптимизационные задачи, с применением метода многокритериальной оптимизации.
КОНТРОЛЬНЫЕ ВОПРОСЫ
Цель pacчётов не числа, а понимание. Прежде чем
решать задачу подучай, что делать с ее решением.
(Законы Р.Хемннга)
Глава 1
1. Определите понятие модели.
. Каковы особенности физического моделирования?
. Определите понятие математической модели.
. Какие требования предъявляются к математическим моделям?
. Какие существуют методы доказательства адекватности модели?
. На какие виды подразделяют математические модели по характеру отображаемых свойств?
. На какие виды подразделяют математические модели по способам получения или природе рассматриваемых математических переменных?
. Приведите пример формального моделирования.
. В какой зоне пространства параметров максимальная точность формальных моделей?
. Характеристикой каких моделей является мощность множества значений переменных?
. Поясните различие структурных свойств модели и программы, имитирующей модель.
. Поясните понятие блочно-иерархического подхода к моделированию.
. Какие независимые переменные применяются при моделировании на микроуровне и макроуровне?
. Как определяется функционирование системы на метауровне?
Глава 2
1. С какой целью проводились экспериментальные исследования асинхронной машины с опытными образцами роторов?
. В чем принципиальное отличие зависимости динамического момента вращения двигателя от статического?
. На чем основан принцип действия прибора "Память 4", определяющего зависимости скорости и ускорения ротора двигателя в динамических режимах?
. Как,определяются динамические характеристики машины с помощью приставки к осциллографу для регистрации изменений скорости и ускорения ротора двигателя?
. Дайте количественную оценку степени влияния отдельных групп роторных контуров на момент вращения асинхронного двигателя в динамическом режиме.
. Как влияет на динамический момент вращения асинхронного двигателя толщина стали ротора с обмоткой, с пустыми пазами, массивного?
. Как осуществляется опытное определение «скачка гистерезиса» в асинхронной машине?
. Какая доля в создании механической мощности на валу приходится на явление гистерезиса и какая доля - на вихревые токи в роторе?
. Что представляет собой интегральный контур вихревых токов?
. Параметры какого из экспериментальных роторов оказались близки к параметрам массивного ротора?
. Как можно определить параметры интегрального контура вихревых токов?
. Каковы результаты исследования влияния роторных вихревых токов на динамические характеристиеи асинхронного двигателя повышенной частоты, 400 Гц?
Глава 3
1. Запишите уравнения идеализированной асинхронной машины в фазной системе координат.
. Выполните преобразования уравнений идеализированной асинхронной машины из трехфазной системы координат в трехфазную заторможенную.
. Как в математической модели программного комплекса макромоделирования асинхронных машин учитывается влияние роторных вихревых токов?
. Какая методика расчёта вытеснения вихревых токов в стержнях ротора используется в математической модели программного комплекса макромоделирования асинхронных машин?
. Запишите выражения для статических индуктивностей. Какие характеристики используются при их определении?
. Запишите выражения для дифференциальных индуктивностей. Какие характеристики используются при их определении?
. Как определяются в математической модели асинхронной машины энергетические показатели, учитывающие значения токов и напряжений в данный момент времени?
. Запишите в матричной форме уравнения асинхронной машины, с учётом многообразия физических процессов, в фазной заторсоженной системе координат.
. Как в программном комплексе макромоделирования асинхронных машин с учётом динамики используется принцип многоуровневого моделирования?
. Как осуществляется моделирование динамических режимов асинхронной машины при различных формах напряжения питания?
. Какие преимущества даёт использование матрицы динамических параметров при численном решении уравнений, учитывающих многообразие физических процессов в асинхронной машине?
. Какое значение будет иметь магнитный момент асинхронного двигателя при пуске на холостом ходу в установившемся режиме?
ЗАКЛЮЧЕНИЕ
Круг проблем, связанных с решением задач анализа и синтеза электрических машин с учетом динамики достаточно давно исследуется специалистами в области электромеханики. Спектр таких задач весьма широк. В данной работе рассмотрены некоторые аспекты проблематики, связанные с математическим моделированием динамических режимов асинхронных машин. Как говорилось выше, цели моделирования могут быть различными. Программный комплекс макромоделирования асинхронных машин может, например, рассматриваться как часть подсистемы оптимизационного расчетного проектирования асинхронных машин с учетом динамики. Процесс расчетного проектирования представляется состоящим из трех этапов: поиска аналога, поиска прототипа и параметрической оптимизации. На основе программного комплекса макромоделирования асинхронных машин решались задачи параметрической оптимизации. Для выбора проектных решений применялся метод многокритериальной оптимизации, основанный на использовании ЛПτ-последовательности и включающий интерактивный режим, что хорошо согласуется с концепцией построения экспертных систем. ЛПτ-последовательность обеспечивает равномерный обзор пространства параметров при сравнительно небольшом количестве испытаний. При решении задачи многокритериальной оптимизации обосновывается и строится содержательное допустимое множество решений, выделяется из него паретовское подмножество и на последнем определяется лучший вариант решения с позиции всех противоречивых критериев оптимизации.
Подсистема оптимизационного проектирования ломимо макромоделей с учетом динамики включает классическую математическую модель асинхронной машины, разработанную при расчете серии асинхронных двигателей. Возможна раздельная оптимизация режимов «статики» и «динамики», и их совместная оптимизация.
Опыт показал, что учет случайных процессов целесообразно осуществлять на регрессионных моделях, получаемых в результате планирования эксперимента в моделях «динамики».
Эти вопросы предполагается подробно рассмотреть в последующей публикации.
ПРИЛОЖЕНИЕ