Задание на проведение исследований
2.1 Определить аналитически и экспериментально параметры напряжения на выходе различных схем выпрямителей.
2.2 Оценить зависимость коэффициента пульсаций от емкости конденсатора фильтра и сопротивления нагрузки.
2.3 Проанализировать параметры выходного напряжения при наличии схемы стабилизации.
Порядок проведения экспериментов
3.1. Соберем схему измерений, приведенную на рисунке 1.
Выберем трансформатор «ideal» из библиотеки «default», а диод – 1N4001. Установим действующее напряжение источника равным 50 В, частоту – 50 Гц. Выполним моделирование.

Определим амплитуду напряжения на входе выпрямителя (на вторичной обмотке трансформатора) и по формуле вычислить постоянную составляющую выходного напряжения.
Максимальное обратное напряжение U max на диоде однополупериодного выпрямителя равно максимуму входного напряжения. 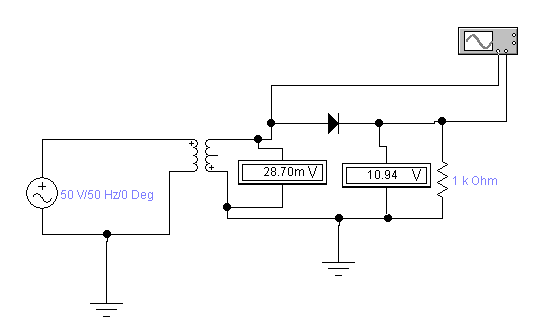
U д = U m / p.
U max =28.70/ 3.14=9.14
Определим частоту сигнала на выходе выпрямителя.
Частота выходного сигнала f выпрямителя вычисляется как величина, обратная периоду выходного сигнала:
f = 1 / T =1/9.14=9.14
Вывод: Расчетные данные практически одинаковы с данными выявленными в ходе исследований показаний.
3.2 Соберем схему измерений, приведенную на рисунке 2.
Установим действующее напряжение источника равным 50 В, частоту – 50 Гц. Выполним моделирование. Занесем в отчет изображение осциллограмм на входе и выходе выпрямителя.

Определим амплитуду напряжения на входе выпрямителя (на половине вторичной обмотки трансформатора) и по формуле вычислить постоянную составляющую выходного напряжения.
U д = 2 U m / p.
U д =33.32/3.14=10.6

Максимальное обратное напряжение U max на каждом диоде двухполупериодного выпрямителя с отводом от средней точки трансформатора равно разности удвоенного максимального значения напряжения на вторичной обмотке трансформатора U 2m и прямого падения напряжения на диоде U ПР:
U max = U 2m – U ПР
U max =33.32-9.8=23.5
Частота выходного сигнала f выпрямителя вычисляется как величина, обратная периоду выходного сигнала:
f = 1 / T =1/23.5
3.3 Соберем схему измерений, приведенную на рисунке 3.
Установим действующее напряжение источника равным 50 В, частоту – 50 Гц. Выполним моделирование.

Определим амплитуду напряжения на входе выпрямителя (на вторичной обмотке трансформатора), если коэффициент трансформации п 2 / п 1 = 1 / 2, и по формуле вычислим постоянную составляющую выходного напряжения.
Среднее значение выходного напряжения U д (постоянная составляющая) мостового выпрямителя вычисляется по формуле:
U д = 2 U 2m / p,=86.7/3.14=27
где максимум вторичного напряжения на полной обмотке трансформатора U 2m вычисляется по формуле:
U 2m = U 1m (n 2 / n 1) = U lm / 2,
U 2m =43.35/ 2=21.6
U 1m - максимальное значение (амплитуда) напряжения на первичной обмотке трансформатора;
п 2 / п 1 – коэффициент трансформации трансформатора питания.

Определим частоту сигнала на выходе выпрямителя.
f = 1 / T =1/21.6
3.4 Соберем схему измерений, приведенную на рисунке 4.
Установить действующее напряжение источника равным 50 В, частоту – 50 Гц. Выполнить моделирование.

При сопротивлении нагрузки, равном 1 кОм, определим среднее значение выходного напряжения и значение коэффициента пульсаций, если емкость конденсатора фильтра принимает значения 10, 50 и 100 мкФ. Результаты вычислений занесем в таблицу.
| 10 мкФ | 50 мкФ | 100 мкФ |
| 17.9 | 20.7 | 21.2 |
Среднее значение выходного напряжения U д выпрямителя с емкостным фильтром может быть приближенно оценено из соотношения:
U д = (U 2max + U 2min) / 2 = U 2max - D U 2 / 2,
U д =(10.6 +31.75)/2=21.2
U д =(31.06+10.5)/2=20.7
U д =(25.5+10.4)/2=17.9
где U 2max и U 2min - максимум и минимум выходного напряжения;
D U 2 = U 2max - U 2min.
При емкости конденсатора фильтра, равной 100 мкФ, определим среднее значение выходного напряжения и значение коэффициента пульсаций, если сопротивление нагрузки принимает значения 2; 1,5; 1 и 0,75 кОм. Результаты вычислений занести в таблицу.
| 2 кОм | 1,5 кОм | 1 кОм | 0,75 кОм |
коэффициент пульсаций e выходного напряжения, который вычислим из соотношения:
e = (D U 2 / U д) × 100%.
e =(21/10.2) × 100%=205
e =(19.9/9.5) × 100%=209
e =(18.83/8.9) × 100%=211
e =(21/9.8) × 100%=214
D U 2 = U 2max - U 2min.
D U 2 = 32-11=21
D U 2 = 29.8-9.9=19.9
D U 2 =28.13-9.3=18.83
D U 2 =31-10=21
постоянная составляющая мостового выпрямителя вычисляется по формуле:
U д = 2 U 2m / p,
U д = 2 U 2m / p,=32/3.14=10.2
U д = 2 U 2m / p,=29.8/3.14=9.5
U д = 2 U 2m / p,=28.13/3.14=8.9
U д = 2 U 2m / p,=31/3.14=9.8
3.5 Соберем схему измерений, приведенную на рисунке 5.
Установим действующее напряжение источника равным 50 В, частоту – 50 Гц. Выполним моделирование.

При сопротивлении нагрузки, равном 1 кОм, определить среднее значение выходного напряжения и значение коэффициента пульсаций, если емкость конденсатора фильтра принимает значения 10, 50 и 100 мкФ. Результаты вычислений занести в таблицу.
| 10 мкФ | 50 мкФ | 100 мкФ |
| 8.4 | 8.8 | 9.2 |
U д = (U 2max + U 2min) / 2 = U 2max - D U 2 / 2,
где U 2max и U 2min - максимум и минимум выходного напряжения;
U д = (10.43+7.2)/2=8.8
U д = (11.22+7.2)/2=9.2
U д = (9.7+7.2)/2=8.4
При емкости конденсатора фильтра, равной 50 мкФ, определим среднее значение выходного напряжения и значение коэффициента пульсаций, если сопротивление нагрузки принимает значения 2; 1,5; 1 и 0,75 кОм. Результаты вычислений занести в таблицу.
| 2 кОм | 1,5 кОм | 1 кОм | 0,75 кОм |
| 118.5 | 119.7 | 118.7 | 120.5 |
e = (D U 2 / U д) × 100%.
e =(4.15/3.5) × 100%=118.5
e =(4.43/3.7) × 100%=119.7
e =(3.73/3.14) × 100%=
e =(4.46/3.7) × 100%=120.5
D U 2 = U 2max - U 2min.
D U 2 =11.25 -7.1=4.15
D U 2 = 11.63-7.2=4.43
D U 2 =10.83-7.1=3.73
D U 2 =11.66-7.2=4.46
U д = 2 U 2m / p,
U д = 2 U 2m / p,=11.25/3.14=3.5
U д = 2 U 2m / p,=11.63/3.14=3.7
U д = 2 U 2m / p,=10.83/3.14=3.4
U д = 2 U 2m / p,=11.66/3.14=3.7