Пример выполнения лабораторной работы №3
«Регрессионный анализ»
Вход в пакет STATISTICA и создание новой таблицы.
Ввод исходных данных и присвоение имен скопированным переменным
В результате выполнения ЛР2 (ДА) выявилась зависимость между значениями средних и номерами уровней факторов. Необходимо определить вид этой зависимости, определив коэффициенты уравнения регрессии. А затем проверить их значимость и адекватность полученной модели, т.е. провести регрессионный анализ.
Для проведения этого анализа следует из предыдущей работы записать в новую таблицу столбцы со средними значениями (YSR) и номерами уровней фактора (URFAC), а также значения дисперсии воспроизводимости (SVOS), количество уровней фактора (u) и число параллельных опытов(m).
3. Построение графика зависимости средних значений (YSR) от уровней фактора (URFAC). YSR=f(URFAC).
3.1.Выбрать пункты меню «Графика», «2М Графики» и «Линейные графики».
3.2.Затем следует выбрать переменные YSR,URFAC.
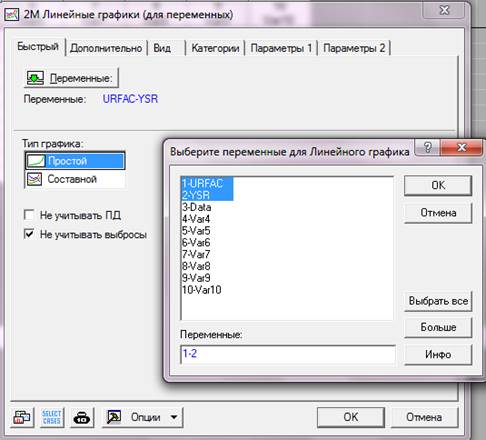
3.3.Можно выбрать закладку «Дополнительно» и установить линейную подгонку.
3.4. В результате получен линейный график с линией регрессии.
Выбор уравнения регрессии и расчет его коэффициентов.
4.1.Выбрать «Анализ», «Множественная регрессия».
4.2.Установить имена переменных.
4.3.Результат ы проведения регрессионного анализа.
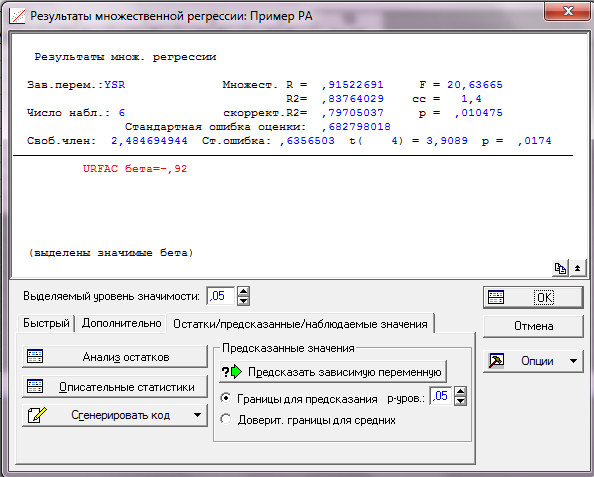
4.4.Выбрать «Анализ остатков», а затем в открывшемся окне выбрать «Итоги регрессии».
В результирующей таблице представлены коэффициенты уравнения регрессии (столбец В) и наблюдаемые значения критерия Стьюдента (столбец t(4)) для каждого коэффициента с указанием числа степеней свободы.
|
|
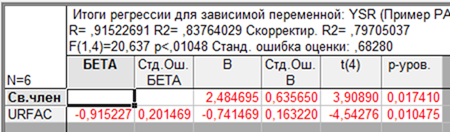
Эти данные следует внести в столбец таблицы обработки данных с соответствующими обозначениями в столбец «Коэффициенты и критерии» (K&K).
На основании полученных результатов записать уравнение регрессии:
YSR = -0,7415*URFAC + 2,4847
Необходимо проверить, значимы ли полученные коэффициенты.
Проверка значимости коэффициентов уравнения регрессии по критерию Стьюдента.
Для проверки значимости определить с помощью «Вероятностного калькулятора» теоретические значения левосторонней и правосторонней критических областей.
Для коэффициента k=-0,7415 tнабл=-4,5428 < tтеор=-2,1319.
Следовательно, коэффициент k значим, так как tнабл находиться в левосторонней критической области и гипотеза о его равенстве нулю отвергается.
Для коэффициента b=2,4847 tнабл=3,909 > tтеор=2,1319.
Следовательно, коэффициент b значим, так как tнабл находиться в правосторонней критической области и гипотеза о его равенстве нулю отвергается.
6. Построение графика разброса данных относительно предполагаемой зависимости.
В окне «Анализ остатков» закладка «Диаграммы рассеяния» выбрать «Две переменные» и задать имена переменных по горизонтали и вертикали.
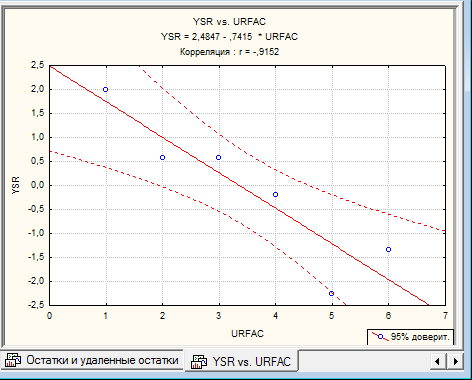
7. Проверка адекватности математической модели по критерию Фишера.
7.1. Для проверки адекватности вернуться в окно «Анализ остатков» и выбрать «Остатки и предсказанные»
7.2. Результаты проведения регрессионного анализа:
Данная таблица - это таблица существующих значений средних, и ожидаемых средних при подстановке полученных коэффициентов в уравнение регрессии и разниц между ними в виде остатков.
|
|
7.3. Скопировать столбец «Остатки» под именем RES в свою таблицу. Этот столбец будет использоваться для проверки адекватности полученной математической модели.
7.4. Создать новый столбец с именем SAD для расчета квадратов отклонений.
7.5. Найти сумму квадратов отклонений. Для этого выбрать «Описательные статистики».
Выбрать переменную (столбец SAD) и функцию «Сумма».
Записать полученный результат в столбец PAD – проверка адекватности под именем SUMSAD.
7.6. Рассчитать дисперсию адекватности SAD2=(m/(u-d))·SUMSAD, где d - число значимых членов уравнения регрессии. Занести это значение через строчку от SUMSAD.
SAD2=(20/(6-2))*1,8649=9,3245
7.7. FEXP=SAD2/SVOSP. Занести это значение через строчку от SAD2.
FEXP=9,3245/8,0953 = 1,1518
7.8. Найти с помощью вероятностного калькулятора теоретическое значение критерия Фишера FTEOR для следующих параметров:
- число степеней свободы числителя df1 = U-d =6-2=4;
- число степеней свободы знаменателя df2 – U(m-1)=6*(20-1) = 114;
- доверительная вероятность p-0.95.
Занести это значение через строчку от FEXP
FTEOR = 2,451273
Таблица обработки в итоге имеет следующий вид:
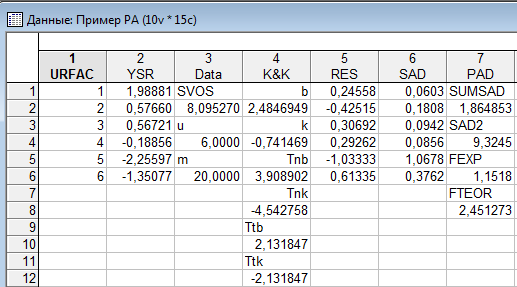
Выводы:
FEXP=1,1518 < FTEOR = 2,4512
Следовательно, математическая модель (уравнение регрессии) адекватна исходным данным.
Примечание.
1). Если 
то математическое описание однозначно адекватно описывает экспериментальные данные.
2). Если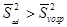 
(SAD2>SVOSP) и Fexp < Fteor, то гипотеза об адекватности не отвергается, и поправки не нужны.
Если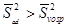 
и Fexp > Fteor, то гипотеза об адекватности отвергается и нужны поправки к уравнению регрессии..
|
|