P 0 = 0!= 1.
Размещением из n элементов по k называется упорядоченный набор из k элементов, выбранных из данных n элементов (k £ n). Два размещения из n элементов по k отличаются друг от друга либо порядком, либо составом своих элементов. Число всех возможных размещений из n по k равно
 .
.
Число всевозможных перестановок из n элементов по k, в которых элементы могут повторяться, равно n k.
Сочетанием из n элементов по k называется неупорядоченный набор из k элементов, выбранных из данных n элементов (k £ n). Два сочетания отличаются друг от друга только составом своих элементов. Число сочетаний из n элементовпо k равно

Приведенные выше сведения из комбинаторики представлены в следующей схеме.
| Нет |
| Нет |
| Нет |
| Испытание – извлечение (выборка) k элементов из n различных элементов (k £ n); N – число всех исходов испытания. |
| Выборка с возвращением? |
| Выборка с учетом порядка элементов? |
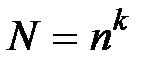
|
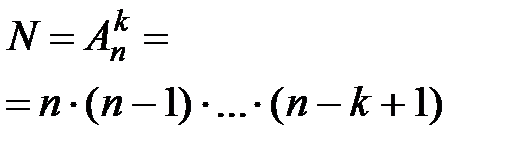
|
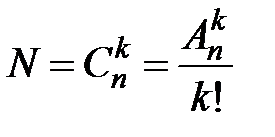
|
| Да |
| Да |
| Нет |
| Нет |
Классическая схема подсчета вероятностей пригодна для решения многих практических задач. Рассмотрим, например, некоторое множество из n элементов, среди которых по некоторому признаку выделено подмножество из n 1 элементов (n 1 £ n), которые назовем “отмеченными”. Это могут быть изделия (годные и бракованные), семена (всхожие и нет) и т. п. Из этого множества элементов наугад без возвращения извлекаются k элементов. Тогда вероятность 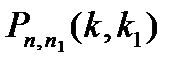 того, что в выборке будет ровно k 1 “отмеченных” элементов (k 1 £ k) определяется по формуле гипергеометрических вероятностей:
того, что в выборке будет ровно k 1 “отмеченных” элементов (k 1 £ k) определяется по формуле гипергеометрических вероятностей:
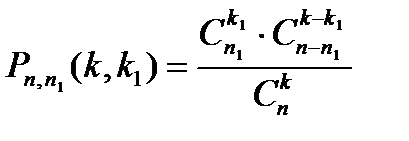 .
.
Пример 2.1. В примерах 1.2 – 1.9 (тема 1) вычислить вероятности всех событий.
Решение примера 1.2. По классическому определению вероятности

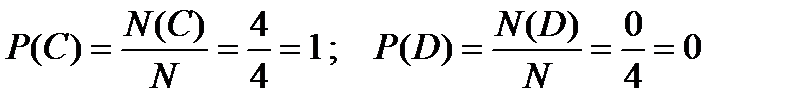 . g
. g
Решение примера 1.3. Здесь мы также имеем классическую схему, согласно которой
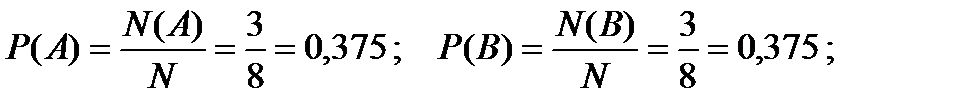
 .
.
Решение примера 1.4.
Пример 2.2. На пяти карточках написаны цифры 1, 2, 3, 4, 5. Наугад берутся три карточки и кладутся в ряд. Чему равна вероятность того, что полученное таким образом трехзначное число окажется: а) не больше 400; b) четным?
Решение (непосредственный подсчет вероятностей). Испытание – извлечение (без возвращения) из 5 карточек трех и расположение их в ряд. Обозначим через A и B события, описанные в п.п. а) и b) примера. Пусть i 1 – 1-я цифра слева, i 2 – 2-я цифра слева и i 3 – 3-я цифра слева полученного трехзначного числа. Тогда
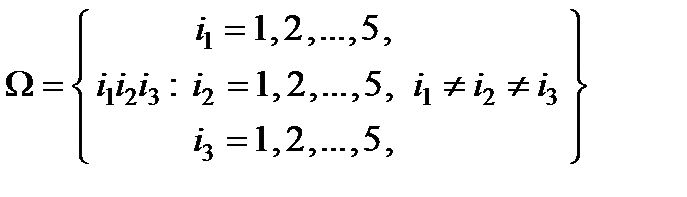 и
и
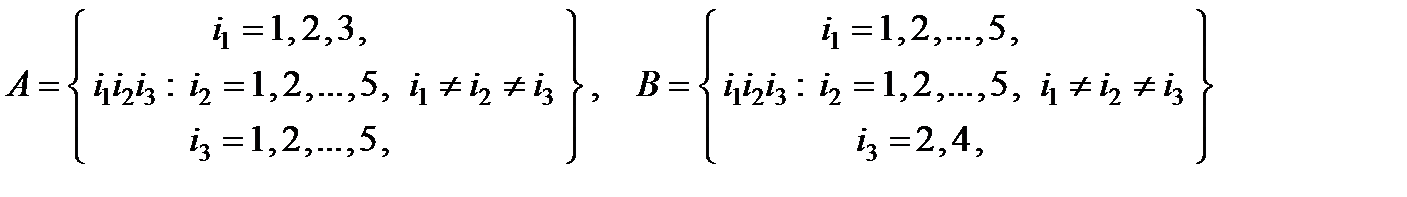 .
.
Для нахождения N = N (W), N (A) и N (B) воспользуемся правилом умножения. Пусть k -е действие состоит в извлечении k -й карточки (k = 1, 2, 3). Поскольку карточки берутся без возвращения, то N (W) = 5 × 4 × 3 = 60, N (A) = 3 × 4 × 3 = 36 и N (B) = 2 × 4 × 3 = 24. Следовательно,
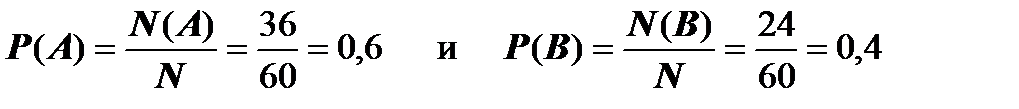 . g
. g
Пример 2.3. Из пяти карточек с буквами А, Б, В, Г, Д наугад одна за другой выбираются три и располагаются в ряд. Какова вероятность того, что получится слово “ДВА”?
Решение (комбинаторный метод вычисления вероятности). Испытание состоит в том, что из пяти карточек последовательно выбираются три и выкладываются в ряд. Число всех элементарных исходов данного испытания – это число всевозможных слов из трех букв (как осмысленных, так и бессмысленных), которые можно составить из имеющихся пяти букв, т.е. число различных упорядоченных комбинаций (размещений) из 5 букв длиной в 3 буквы:
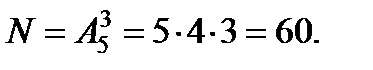
Рассмотрим событие А = {получится слово “ДВА”}. Вероятность этого события вычислим по классическому определению. Из полученных N = 60 всевозможных слов длиной в три буквы благоприятствующим событию А является только одно: слово “ДВА”. Следовательно, N (A) =1 и  g
g
Пример 2.4. В условиях примера 2.2 имеются три карточки с цифрой 1, две карточки с цифрой 2 и по одной карточке с цифрами 3, 4, 5.
Решение. Испытание –
Пример 2.5. На шести карточках разрезной азбуки написаны 3 буквы А, 2 буквы Н и одна буква С. Ребенок, не умеющий читать, раскладывает эти карточки в ряд. Какова вероятность того, что у него получится слово “АНАНАС”?
Решение. Испытание – выкладывание в ряд 6 букв, что эквивалентно, очевидно, извлечению (без возвращения) из имеющихся карточек шести и расположению их в ряд. Обозначим через A событие, состоящее в том, что получится слово “АНАНАС”.
1-й способ (непосредственный подсчет вероятности).
Пусть xi – i -я буква слева, полученного слова (осмысленного или бессмысленного), i = 1, 2, …, 6. Тогда
 и
и
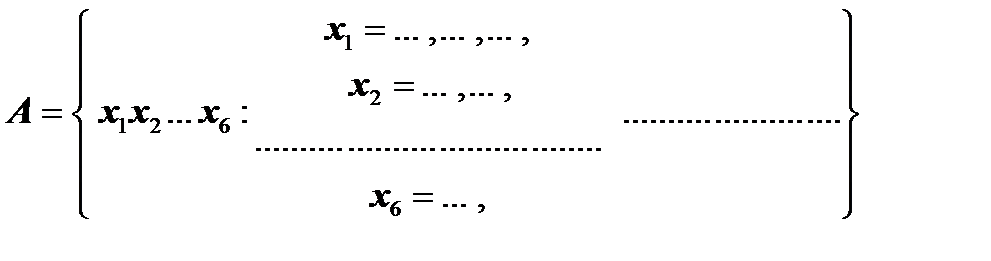 .
.
Воспользовавшись правилом умножения, находим N (W) = ……………………… и N (A) = ………………………….. Следовательно, P (A) = ……………………………..
2-й способ (комбинаторный метод вычисления вероятности).
Пример 2.6. В лифт девятиэтажного дома на первом этаже вошли 4 человека. Каждый из них (независимо от других) может выйти на любом из этажей, начиная со второго. Найти вероятность того, что:
a) все пассажиры выйдут на разных этажах;
b) все пассажиры выйдут на одном этаже;
с) два пассажира выйдут на одном этаже, а двое других – на разных этажах.
Решение. Испытание – выход 4 человек на случайным образом выбираемом каждым из них этаже дома (со 2-го по 9-й). Пусть A, B и C – события, описанные в п.п. a), b) и c).
1-й способ (непосредственный подсчет вероятностей).
2-й способ (комбинаторный метод вычисления вероятностей).
Пример 2.7. За круглым столом случайным образом рассаживаются 10 человек, среди которых находится одна супружеская пара. Определить вероятность того, что муж с женой окажутся рядом.
2.8. В условиях задачи 2.7 люди рассаживаются вдоль одной стороны прямоугольного стола.
2.9. Группа из 6 мальчиков и 6 девочек делится случайным образом на две равные подгруппы. Найти вероятность того, что:
а) в каждой подгруппе число мальчиков и девочек будет одинаковым;
b) в какой-либо подгруппе мальчиков будет больше, чем девочек.
Пример 2.10. Двенадцать человек, среди которых 6 юношей и 6 девушек, случайным образом группируются попарно. Определить вероятность того, что:
а) все десять пар будут состоять из лиц разного пола;
b) будет хотя бы одна пара, состоящая из лиц разного пола.
2.11. Брошены три монеты. Найти вероятности событий:
а) A = {первая монеты выпала гербом};
б) B = {выпало ровна два герба};
в) C = {Выпало не больше двух гербов}.
2.12. Ребенок играет с 10 буквами разрезной азбуки: А, А, А, Е, И, К, М, М, Т, Т. Какова вероятность того, что при случайном расположении букв в ряд он получит слово МАТЕМАТИКА?
2.13. Бросаются 4 игральные кости. Найти вероятность того, что на них выпадет по одинаковому числу очков.
2.14. В ящике 10 красных и 6 синих пуговиц. Какова вероятность того, что две наудачу вынутые пуговицы будут одноцветными?
2.15. В урне имеется 5 белых, 6 черных и 4 красных шара. Из урны наугад одновременно извлекают 3 шара. Какова вероятность того, что все шары будут:
а) одного цвета;
б) разных цветов?
2.16. Колода игральных карт (52 листа, 4 масти по 13 карт в каждой) тщательно перетасована. Наудачу берут 6 карт (без возвращения). Найти вероятности того, что среди этих карт
а) окажется король пик;
б) окажутся представители всех мастей;
в) будет ровно 5 карт одной масти.
2.17. Из колоды (52 листа) наудачу вынимаются три карты. Найти вероятности того, что:
а) среди них окажется ровно один туз;
б) среди них окажется хотя бы один туз;
в) это будут тройка, семерка и туз (в любом порядке).
2.18. Колоду карт (36 листов) наудачу разделяют на две равные пачки. Чему равна вероятность, что:
а) в каждой из пачек окажется по два туза;
б) в одной из пачек окажется все четыре туза;
в) в пачках окажется по равному числу красных карт?
2.19. Числа 1, …, n расположены в случайном порядке. Найти вероятность того, что числа
а) 1 и 2; б) 1, 2 и 3
расположены рядом в указанном порядке.
2.20. На полке в случайном порядке расставлено n книг, среди которых находится двухтомник Д. Лондона. Предполагая, что различные расположения книг равновероятны, найти вероятность того, что оба тома расположены рядом.
2.21. Цифры 1, 2, 3, 4 и 5 написаны на пяти карточках. Наудачу вынимаются по одной три карточки и кладутся рядом слева направо. Какова вероятность того, что полученное число окажется четным?
2.22. Из цифр 1, 2, 3, 4 и 5 сначала выбирают одна, а затем из оставшихся четырех – вторую. Найти вероятность того, что:
а) в первый раз; б) во второй раз; в) оба раза
будет выбрана нечетная цифра.
2.23. Ящик содержит 90 годных и 10 дефектных шурупов. С какой вероятностью среди десяти наудачу взятых шурупов нет дефектных?
2.24. Найти вероятность того, что:
а) дни рождения 12 человек придутся на 12 разных месяцев года (предполагается, что все месяцы равновероятны);
б) дни рождения 6 человек придутся в точности на два месяца.
2.25. Бросаются 5 игральных костей. Найти вероятность того, что по меньшей мере на
а) двух; б) трех
из них выпадут одинаковые грани.
2.26. В купейный вагон (9 купе по 4 места) семи пассажирам продано семь билетов. Найти вероятность того, что оказались занятыми
а) ровна два купе; б) ровно три купе.
ТЕМА 3. ГЕОМЕТРИЧЕСКОЕ ОПРЕДЕЛЕНИЕ ВЕРОЯТНОСТИ
Предположим, что пространство элементарных исходов W, соответствующее рассматриваемому испытанию, бесконечно и несчетно, а его элементы являются равновозможными. Пусть множество W представляет собой некоторую область в n -мерном пространстве, имеющую конечную меру m (W):  , m (W) < ¥. Под мерой m (А)множества А понимается его длина в одномерном случае (n = 1), т.е. если множество на прямой; площадь множества в двумерном случае (n = 2), т.е. если оно на плоскости; объем – в трехмерном случае (n = 3), т.е. если множество в пространстве и т. д. Тогда, согласно геометрическому определению вероятности, вероятность события А равна отношению меры m (А) множества А к мере m (W) всего пространства элементарных исходов:
, m (W) < ¥. Под мерой m (А)множества А понимается его длина в одномерном случае (n = 1), т.е. если множество на прямой; площадь множества в двумерном случае (n = 2), т.е. если оно на плоскости; объем – в трехмерном случае (n = 3), т.е. если множество в пространстве и т. д. Тогда, согласно геометрическому определению вероятности, вероятность события А равна отношению меры m (А) множества А к мере m (W) всего пространства элементарных исходов:
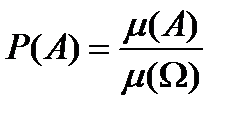 .
.
Пример 3.1. В примере 1.11 (тема 1) найти вероятности событий A, B, …, E.
Пример 3.2. На перекрестке установлен автоматический светофор, в котором одну минуту горит зеленый свет и полминуты – красный, затем снова одну минуту – зеленый и полминуты – красный и т. д. В случайный момент времени к перекрестку подъезжает автомобиль. Какова вероятность того, что он проедет перекресток без остановки?
Решение. Испытание – фиксация момента подхода автомобиля к перекрестку (в минутах), начиная с момента загорания зеленого света. Элементарный исход испытания – число x (мин) и W = { x: 0 £ x £ 1,5}. Введем событие A = {автомобиль проедет перекресток без остановки} = { x: 0 £ x £ 1,0}. Так множество W на вещественной прямой, то согласно геометрическому определению вероятности
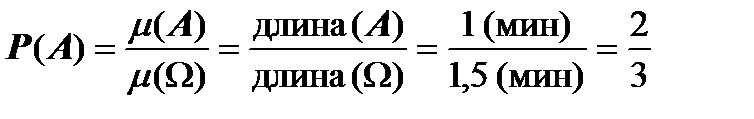 . g
. g
Пример 3.3. Во время грозы между двумя населенными пунктами M и N, отстоящими друг от друга на 31 км, в неизвестном месте произошел обрыв электрического провода. Для обнаружения и устранения аварии из пункта M выходит ремонтная бригада и двигается вдоль линии электропередачи с постоянной скоростью 4 км/час. Через час после выхода 1-й бригады из пункта N выходит 2-я бригада и двигается навстречу 1-й со скоростью 5 км/час. Определить вероятность того, что:
a) 1-я бригада обнаружит место обрыва раньше 2-й;
b) 2-я бригада обнаружит место обрыва раньше 1-й;
c) обе бригады обнаружат место обрыва одновременно.
Предполагается, что место обрыва электрического провода равновозможно любое между пунктами M и N.
Решение. Испытание –
Пример 3.4. Внутрь круга радиуса R наудачу брошена точка. Найти вероятность того, что точка окажется вписанного в круг: а) квадрата; b) правильного треугольника.
Пример 3.5. Стержень длины L см. наудачу ломается в двух местах. Найти вероятность того, что из получившихся трех частей можно составить треугольник.
Решение. Пусть х (см) – длина одной части, у (см) – длина другой части; тогда длина третьей части равна L – (x + y) (см). Следовательно, любой исход испытания, состоящего в разломе стержня на три части, определяется парой чисел (х, у),удовлетворяющих условиям 0 < х < L, 0 < у < L, х+у < L. Иначе говоря, в качестве пространства элементарных исходов Ω, соответствующего рассматриваемому испытанию, можно выбрать следующее множество на плоскости:
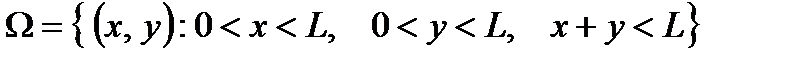 .
.
Пусть событие А состоит в том, что из полученных кусков можно составить треугольник. Для этого необходимо, чтобы сумма длин любых двух кусков была больше длины третьей:

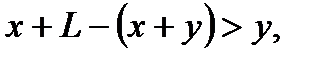

Преобразовав эти неравенства, получим
 .
.
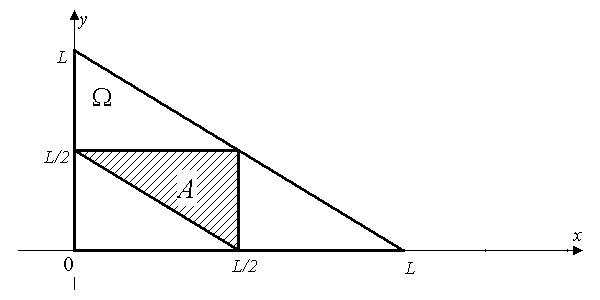
Рис. 3.1.
На рис. 3.1 изображены области Ω и А, которые представляют собой, очевидно, треугольники на плоскости. Тогда по геометрическому определению вероятности

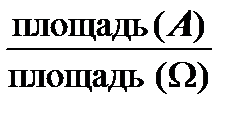 =
=  g
g
3.6. В одной из игр игрок бросает монету наудачу на поверхность стола, разграфленную параллельными линиями, отстоящими друг от друга на расстоянии 2 a. Если монета радиуса r < a не пересечет ни одной из прямых, то игрок получает награду, в противном случае он теряет свою монету. Какова вероятность выигрыша? (Если монета падает со стола, то попытка не считается).
3.7. Та же игра, но теперь стол имеет квадратную сетку со стороной 2 а и для выигрыша нужно попасть внутрь квадрата. Каковы шансы выиграть?
3.8. Два парохода должна подойти к одному и тому же причалу. Время прихода обоих пароходов независимо и равновозможно в течение суток. Определить вероятность того, что одному из пароходов придется ожидать освобождение причала, если время стоянки 1-го парохода 2 часа, а 2-го – 4 часа.
ТЕМА 4. ТЕОРЕМЫСЛОЖЕНИЯ И УМНОЖЕНИЯ ВЕРОЯТНОСТЕЙ
Теоремы сложения вероятностей:
1. Если события А и В несовместны, то 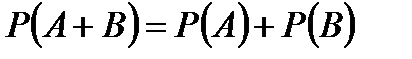 .
.
2. Если события А и В совместны, то 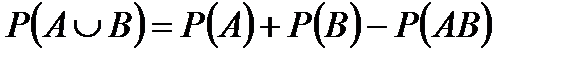 .
.
3. Если события 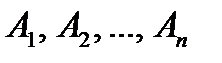 попарно несовместны, то
попарно несовместны, то
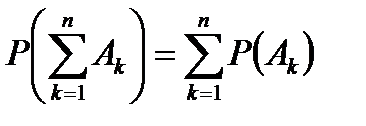 .
.
4. Если события 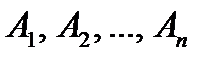 не являются попарно несовместными, то
не являются попарно несовместными, то
 .
.
Теоремы умножения вероятностей:
1. Если события А и В независимы, то P (A × B) = P (A) × P (B).
2. Если события А и В зависимы, то 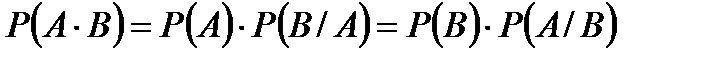 .
.
3. Если события 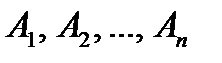 взаимно независимы (независимы в совокупности), то
взаимно независимы (независимы в совокупности), то
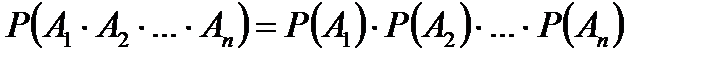 .
.
4. Если события 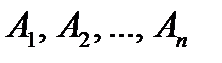 не являются взаимно независимыми, то
не являются взаимно независимыми, то

Пример 4.1. Для сигнализации об аварии в офисе некоторой фирмы установлены три сигнализатора различных типов, которые работают независимо друг от друга. Известно, что при аварии сигнализатор первого типа срабатывает в среднем в 95% всех аварий, второго типа – в 90%, третьего – в 80%. Найти вероятность того, что при аварии:
a) сработает только один сигнализатор;
b) сработают два сигнализатора;
c) сработают не менее двух сигнализаторов;
d) сработает хотя бы один сигнализатор;
e) все сигнализаторы поведут себя одинаково, т.е. либо сработают, либо нет.
Решение. Испытание – проверка функционирования трех сигнализаторов во время аварии. Пусть A, B, …, E – события, описанные в п.п. a), b), …, e) примера 4.1. Введем также следующие события:
Ai = {во время аварии сработает i –й сигнализатор}, i = 1, 2, 3.
По формулам классического определения вероятности и вероятности противоположного события находим
P (A 1) = 0,95, 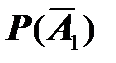 = 1 – P (A 1) = 0,05; P (A 2) = 0,9,
= 1 – P (A 1) = 0,05; P (A 2) = 0,9,  = 1 – P (A 2) = 0,1;
= 1 – P (A 2) = 0,1;
P (A 3) = 0,8,  = 1 – P (A 3) = 0,2.
= 1 – P (A 3) = 0,2.
Кроме того, по условию события А 1, А 2, А 3 независимы.
a) Событие А произойдет, если произойдет какое-либо одно из следующих трех попарно несовместных событий:
сработает 1-й сигнализатор, а 2-й и 3-й не сработают – это событие  ;
;
сработает 2-й сигнализатор, а 1-й и 3-й не сработают – это событие 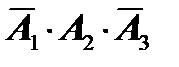 ;
;
сработает 3-й сигнализатор, а 1-й и 2-й не сработают – это событие 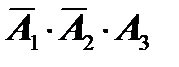 .
.
Следовательно, событие А можно представить в виде суммы трех попарно несовместных событий: А = 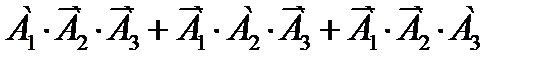 . Используя теорему сложения вероятностей для совокупности попарно несовместных событий и теорему умножения вероятностей для независимых событий, получим
. Используя теорему сложения вероятностей для совокупности попарно несовместных событий и теорему умножения вероятностей для независимых событий, получим
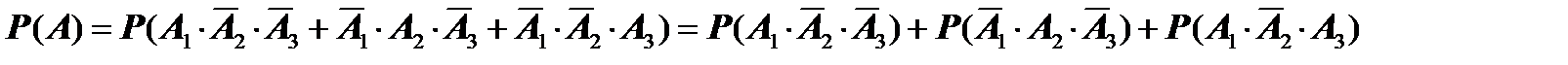
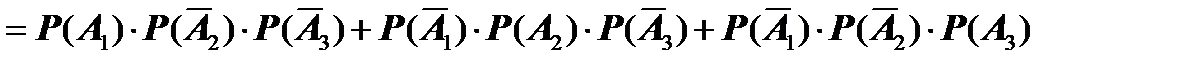 =
=
= 0,95×0,1×0,2 + 0,05×0,9×0,2 + 0,05×0,1×0,8 = 0,032.
b) Событие В означает срабатывание любых двух сигнализаторов их трех, т.е.
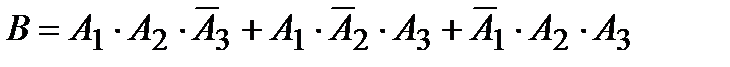 .
.
Снова по теоремам сложения вероятностей для попарно несовместных событий и умножения вероятностей для независимых событий, имеем
 …………………………………………… ………………………………………………………………………………………….= 0,283.
…………………………………………… ………………………………………………………………………………………….= 0,283.
c) Очевидно, событие С наступит, если сработают любые два сигнализатора из трех (событие В) или сработают все три сигнализатора (событие F = A 1× A 2× A 3), т.е. C = B + F. Тогда, снова используя теоремы сложения вероятностей для попарно несовместных событий и умножения вероятностей для независимых событий, получим
 Р (С) = Р (B + F) = Р (B) + Р (F) = …………………………………………… = 0,967.
Р (С) = Р (B + F) = Р (B) + Р (F) = …………………………………………… = 0,967.
d) Событие D представляет сумму несовместных событий А (включающего три варианта) и С (четыре варианта), т.е. D = А + С (семь вариантов). По теореме сложения вероятностей для двух событий находим
Р (D) = Р (А + С) = Р (А) + Р (С) = 0,032 + 0,967 = 0,999.
Можно проще найти вероятность события D, если перейти к противоположному событию, включающему всего один вариант: 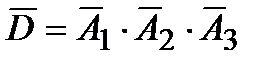 . Применяя формулу для вероятности противоположного события и теорему умножения вероятностей для независимых событий, получим
. Применяя формулу для вероятности противоположного события и теорему умножения вероятностей для независимых событий, получим
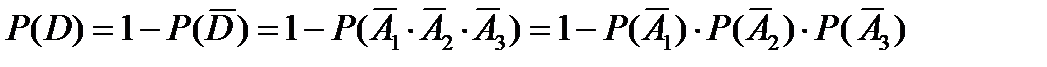 =
=
= 1 – 0,05×0,1×0,2 = 1– 0,001 = 0,999.
Таким образом, срабатывание во время аварии хотя бы одного сигнализатора является практически достоверным событием.
e)
Пример 4.2. Два игрока подбрасывают монету по три раза каждый. Определить вероятность того, что:
a) у игроков будет одинаковое число гербов;
b) у I игрока будет больше гербов, чем у II;
c) у II игрока будет больше гербов, чем у I.
Решение. Испытание – подбрасывание монеты по три раза каждым. Пусть A, B, C – события, описанные в п.п. a), b), c) примера 4.2.
Первый способ (использование классического определения вероятности). Рассматриваемое испытание эквивалентно, очевидно, подбрасыванию монеты 6 раз. Поскольку при каждом подбрасывании монета может выпасть двумя способами, то в силу правила умножения (см. тему 2) всего исходов испытания N = 26 = 64. Используя правила сложения и умножения можно подсчитать количество исходов испытания, благоприятствующих событиям A, B и C: N (A), N (B) и N (C).
Второй способ (применение теорем сложения и умножения вероятностей).
Введем следующие события: A I i = {у I игрока выпадет i гербов}, A II i = {у II игрока выпадет i гербов}, i = 0, 1, 2, 3. Тогда событие A можно тогда представить в следующем виде:
A = A I0 × A II0 + A I1 × A II1 + A I2 × A II2 + A I3 × A II3,
где слагаемые являются попарно несовместными, а сомножители – независимыми событиями. Применяя теорему сложения вероятностей для попарно несовместных событий и теорему умножения вероятностей для независимых событий, получаем
P (A) = P (A I0) P (A II0) + P (A I1) P (A II1) + P (A I2) P (A II2) + P (A I3) P (A II3).
Вычисление отдельных вероятностей в последнем выражении опять же можно произвести двумя способами: непосредственным (используя классическое определение вероятности при 3-х кратном подбрасывании монеты) и с помощью теорем сложения и умножения вероятностей.
Пример 4.3. На стеллаже библиотеки в случайном порядке расставлено 15 учебников, причем 5 из них в твердом переплете, а остальные – в мягком. Библиотекарь берет наудачу три учебника. Найти вероятность того, что из взятых учебников:
a) только один будет в твердом переплете;
b) два будут в твердом переплете;
c) не менее двух будут в твердом переплете;
d) хотя бы один будет в твердом переплете;
e) все будут в одинаковых переплетах.
Решение. Испытание – из 15 книг наудачу берутся 3 книг (без возвращения и без учета порядка следования книг среди отобранных). Следовательно, число всевозможных исходов данного испытания равно числу сочетаний из 15 по 3:
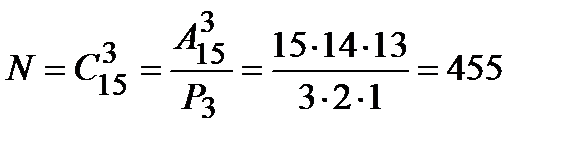 .
.
Обозначим через A, B, …, E – события, описанные в п.п. a), b), c), …, e) примера 4.2. Определим также следующие события:
Ai = {среди отобранных 3 книг i книг в твердом переплете}, i = 0, 1, 2, 3.
Найдем вероятности событий Ai (i = 0, 1, 2, 3) по формуле гипергеометрических вероятностей при n = 15 (все учебники на стеллаже), n 1 = 5 (книги в твердом переплете на стеллаже), k = 3 (взятые книги со стеллажа) и k 1 = i = 0, 1, 2, 3 (книги в твердом переплете среди взятых):
 , i = 0, 1, 2, 3.
, i = 0, 1, 2, 3.
Отсюда

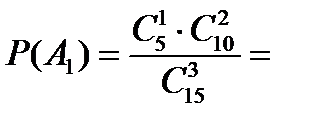 …………… = …………… = 0,494;
…………… = …………… = 0,494;
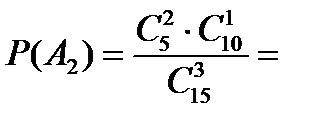 …………… = …………… = 0,220;
…………… = …………… = 0,220;
P (A 3) = ……… = ………………= …………… = 0,022.
а) Очевидно, интересующее нас событие А = А 1, поэтому P (A) = P (A 1) = 0,494.
b) Аналогично, событие B = А 2, поэтому P (B) = P (A 2) = 0,2240.
c) Событие C произойдет, если два учебника будут в переплете (это событие А 2) или три учебника будут в переплете (это событие А 3). Следовательно, событие C можно представить в виде суммы двух несовместных событий: C = А 2 + А 3. Тогда по теореме сложения вероятностей для двух несовместных событий имеем
Р (C) = ………………………………………………………. = 0,242.
d) Первый способ. Событие D произойдет, если произойдет любое из следующих трех несовместных событий:
будет один учебник в твердом переплете – это событие А 1;
будут два учебника в твердом переплете – это событие А 2;
будет три учебника в твердом переплете – это событие А 3.
Следовательно, событие D можно представить в виде суммы трех попарно несовместных событий: D = A 1 + А 2 + А 3. Тогда по теореме сложения вероятностей для совокупности попарно несовместных событий имеем
Р (D) = Р (A 1+ А 2 + А 3) = Р (A 1) + Р (А 2) + Р (А 3) = 0,494 + 0,220 + 0,022 = 0,736.
Второй способ. События D и А 0 являются противоположными, т.е. А 0 = 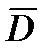 , поэтому Р (D) = 1 –
, поэтому Р (D) = 1 – 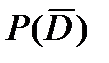 = 1 – Р (А 0) = 1 – 0,264 = 0,736.
= 1 – Р (А 0) = 1 – 0,264 = 0,736.
e)
Пример 4.4. В коробке имеется 12 электролампочек, среди которых 4 бракованные, неотличимые по виду от доброкачественных. Некто наугад берет электролампочку, ввинчивает ее в патрон и включает ток. Бракованная лампочка сразу же перегорает; она выбрасывается и проверяется следующая. И так до тех пор, пока не будет гореть лампочка. Найти вероятность того, что будет выброшено не более двух электролампочек.
Решение. Испытание состоит в том, что поочередно (и без повторения) проверяются электролампочки до тех пор, пока не будет обнаружена доброкачественная. Пусть событие А заключается в том, что будет выброшено не более двух электролампочек, т.е. количество выброшенных лампочек равно 0, 1 или 2. Это событие, очевидно, эквивалентно тому, что будет удачной первая, вторая или третья попытка замены лампочки. Обозначим через 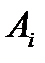 событие, состоящее в том, что i- ялампочка доброкачественная, i = 1, 2, 3.Тогда событие А можно представить в виде
событие, состоящее в том, что i- ялампочка доброкачественная, i = 1, 2, 3.Тогда событие А можно представить в виде
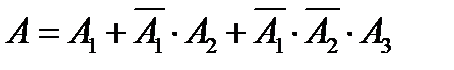 ,
,
где слагаемые являются попарно несовместными событиями. Применяя вначале теорему сложения вероятностей для несовместных событий, а затем теорему умножения вероятностей для зависимых событий, находим
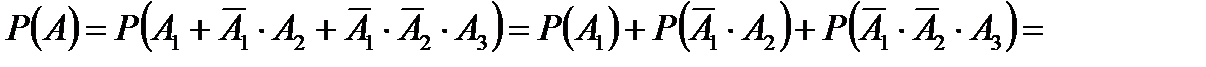

 g
g
Пример 4.5. Имеется коробка с девятью новыми теннисными мячами. Для игры берут наугад три мяча, и после игры их кладут обратно. Какова вероятность того, что после трех игр в коробке не останется неигранных мячей? Предполагается, что при выборе мячей игранные от неигранных не отличаются.
Решение. Испытание – выбор трех мячей из девяти для трех игр, т.е. три раза, с возвращением мячей обратно в коробку. Пусть событие А состоит в том, что после трех игр все мячи в коробке будут игранными.
Первый способ (классическое определение вероятности).
Первое действие – выбор для 1-й игры 3 мячей (без возвращения и без учета порядка) из 9 мячей в коробке – может быть осуществлено 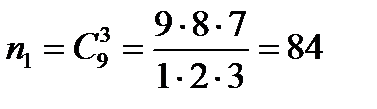 способами; 2-е действие – выбор для 2-й игры 3 мячей (без возвращения и учета порядка) из 9 мячей – может быть осуществлено
способами; 2-е действие – выбор для 2-й игры 3 мячей (без возвращения и учета порядка) из 9 мячей – может быть осуществлено 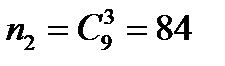 способами; наконец, 3-е действие – выбор для 3-й игры 3 мячей (без возвращения и учета порядка) из 9 мячей – может быть осуществлено также
способами; наконец, 3-е действие – выбор для 3-й игры 3 мячей (без возвращения и учета порядка) из 9 мячей – может быть осуществлено также  способами. Согласно правилу умножения число всевозможных исходов рассматриваемого испытания равно
способами. Согласно правилу умножения число всевозможных исходов рассматриваемого испытания равно
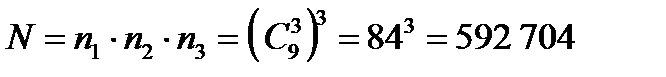 .
.
Аналогичным образом находим N (A) = ……………………… и
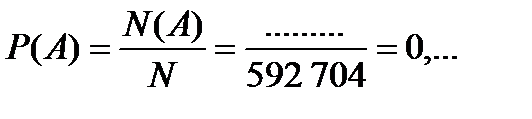 .
.
Второй способ (теоремы сложения и умножения вероятностей).
Событие А можно представить в виде произведения трех зависимых событий: А = А 1× А 2× А 3, где событие Аi = {взятые для i -й игры три мяча – новые}, i = 1, 2, 3. Тогда…
Пример 4.6. В урне 3 белых и 4 черных шара. Два игрока поочередно вынимают из урны наудачу по шару, не вкладывая их обратно. Выигрывает тот игрок, который раньше вытащит белый шар. Определить вероятность выигрыша 1-го игрока, т.е. игрока, первым начавшим игру.
Решение. Испытание – из урны, содержащей 7 шаров, два игрока поочередно вынимают по одному шару, не возвращая их обратно, до тех пор, пока не будет вытащен белый шар. Пусть событие A = {1-й игрок первым вытащит белый шар}.
4.7. Завод выпускает изделия определенного вида, причем 5% продукции завода в среднем составляет брак. Изделия осматриваются одним контролером; он обнаруживает имеющийся брак в среднем в 95% всех проверок. Если брак не обнаружен, изделие пропускается в готовую продукцию. Кроме того, контролер может по ошибке забраковать не бракованное изделие, что происходит в среднем в 7% всех проверок. Определить вероятность того, что изделие, наудачу выбранное из продукции завода, будет:
a) забраковано; b) забраковано ошибочно;
c) пропущено в готовую продукцию с браком.
Пример 4.8. Завод выпускает изделия определенного вида, причем 5% продукции завода в среднем составляет брак. После изготовления изделия последовательно осматриваются 4 контролерами; k -й контролер обнаруживает брак, если он имеется, в среднем в (91 + k)%, k = 1, 2, 3, 4, всех проверок. Определить вероятность того, что изделие, наудачу выбранное из продукции завода, будет забраковано:
a) всеми контролерами; b) только четвертым контролером;
b) каким-либо одним контролером; d) хотя бы одним контролером.
Пример 4.9. Уходя из квартиры, восемь гостей, имеющих одинаковые размеры обуви, надевают туфли в темноте. Каждый из них может отличить правую туфлю от левой, но не может отличить свою от чужой. Найти вероятность того, что каждый гость наденет:
a) свои туфли; b) туфли из одной пары (может быть и не свои).
Пример 4.10. Та же задача, но гости не могут отличить не только свою туфлю от чужой, но и правую от левой и поэтому берут первые две попавшиеся туфли.
ТЕМА 5. ФОРМУЛЫПОЛНОЙ ВЕРОЯТНОСТИ И БАЙЕСА
Предположим, что в результате испытания событие А может произойти вместе с одним из попарно несовместных событий H 1, H 2, …, Hn, составляющих полную группу. Тогда вероятность события А можно найти с помощью формулы полной вероятности
 .
.
Поскольку заранее неизвестно, какое из событий H 1, H 2, …, Hn наступит в результате испытания, их часто называют гипотезами. Необходимым (но не достаточным) условием того, что H 1, H 2, …, Hn образуют полную группу попарно несовместных событий, является выполнение равенства:
 .
.
Пусть до испытания известны априорные (доопытные) вероятности гипотез Р (Н 1), Р (Н 2), …, Р (Нn). После испытания становится известно, что произошло некоторое событие А. Каковы теперь апостериорные (послеопытные) вероятности гипотез при условии, что событие А произошло? Ответ дается формулой Байеса
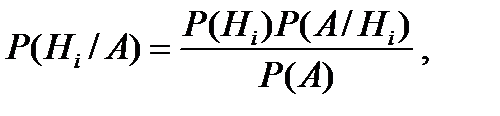 i = 1, 2, …., n,
i = 1, 2, …., n,
где вероятность события А определяется формулой полной вероятности.
Формула Байеса позволяет переоценить вероятности гипотез после поступления новой информации относительно осуществления того или иного события. Апостериорные вероятности, как и априорные, удовлетворяют соотношению
 .
.
Пример5.1. В торговую фирму поступили телевизоры от трех поставщиков в отношении 1:2:3. Практика показала, что телевизоры, поступающие от 1-го, 2-го и 3-го поставщиков, не потребуют ремонта в течение гарантийного срока соответственно в 85%, 90% и 95% случаев.
1). Определить вероятность того, что проданный торговой фирмой телевизор не потребует ремонта в течение гарантийного срока.
2). Проданный телевизор потребовал ремонта в течение гарантийного срока. От какого поставщика вероятнее всего поступил этот телевизор?
Решение. Испытание – проверка качества в течение гарантийного срока купленного в торговой фирме телевизора.
1). Пусть событие А состоит в том, что проданный телевизор не потребует ремонта в течение гарантийного срока. Так как не известно, от какого поставщика проданный телевизор, то введем гипотезы
Нi = {телевизор поступил в торговую фирму от i -го поставщика}, i = 1, 2, 3.
По условию
P (A / H 1) = 0,85; P (A / H 2) = 0,90; P (A / H 3) = 0,95.
Согласно классическому определению вероятности, имеем
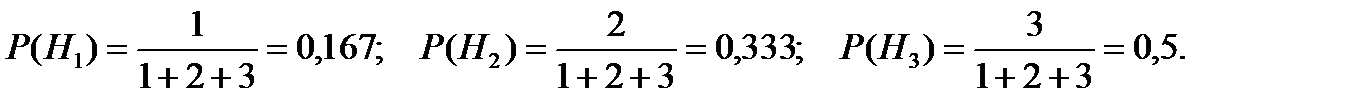
Контроль: P (H 1) + P (H 2) + P (H 3) = 0,167 + 0,333 + 0,5 = 1.
По формуле полной вероятности находим
Р (А) = Р (Н 1) · Р (А / Н 1) + Р (Н 2) · Р (А / Н 2) + Р (Н 3) · Р (А / Н 3) =
 .
.
2). Событие 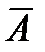 = {телевизор потребует ремонта в течение гарантийного срока};
= {телевизор потребует ремонта в течение гарантийного срока}; 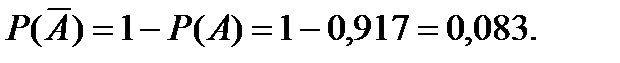
Исходя из условия и свойств условной вероятности, получим
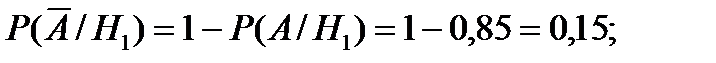

 .
.
По формуле Байеса находим
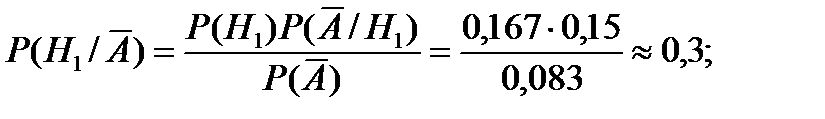


Контроль: 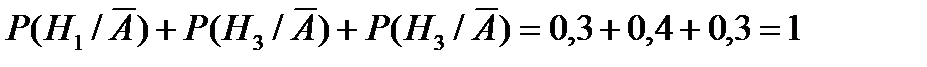 .
.
Таким образом, после наступления события 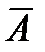 вероятность гипотезы Н<
вероятность гипотезы Н<