Этим методом рекомендуется пользоваться в тех случаях, когда число уравнений в системе меньше числа уравнений, составленных по методу контурных токов. Число уравнений в системе при использовании метода узловых потенциалов равно n = N У –1.
Расчет разветвленной схемы методом узловых потенциалов проводят в несколько этапов.
Если в схеме имеются источники ЭДС, их сначала преобразуют в эквивалентные источники тока I i с использованием формулы преобразования:
I i = E i g i (6)
где g i = 1 / r i есть внутренняя проводимость источника i.
Далее выбирают опорный, базисный узел и принимают его потенциал равным нулю. В качестве такого узла целесообразно выбрать узел, в котором сходится наибольшее число ветвей. Потенциалы в остальных узлах схемы отсчитываются от базисного узла.
Затем составляют и решают систему уравнений относительно узловых потенциалов V i:
 (7)
(7)
где g ii - сумма проводимостей ветвей, присоединенных к узлу i;
g ij - сумма проводимостей ветвей, непосредственно соединяющих узел i с узлом j;
å I i - алгебраическая сумма токов источников тока, присоединенных к узлу i, при этом со знаком плюс берутся те токи, которые направлены к узлу, и со знаком минус – в направлении от узла.
На последнем этапе по найденным узловым потенциалам находят искомые токи в ветвях с помощью закона Ома (1).
Преобразуем нашу схему в соответствии с изложенными выше правилами к виду, показанному на рис. 3.

Рис. 3. Эквивалентная схема разветвленной цепи.
Выберем в качестве опорного базисного узла узел (b). Примем его потенциал равным нулю и составим систему уравнений относительно остальных узловых потенциалов:
 (8)
(8)
где G 24 = 1/(r 2 +R 4 ).
Определив значения потенциалов V a, V c, V d и V fсоответственно для узлов a, c, d и f, воспользуемся законом Ома (2) и рассчитаем значения токов в ветвях нашей схемы:
J 0 = V f G 3; J 1 = (E 1 + V a ) g 1; J 2 = (V c - V a ) G 2;
J 3 = V a G 1; J 4 = (V d - V c ) G n; J 5 = (V c - V f - E 3 ) g 3;
J 6 = (V d - V f ) G 5; J 7 = (E 2 - V d ) G 24
Решение задачи по определению значений токов в схеме методом узловых потенциалов с использованием программы MathCAD приведено на листинге №3.
Правильность расчета проверяется путем проверки выполнения баланса мощностей (4).
Для расчета падений напряжения на элементах электрической цепи следует воспользоваться законом Ома (1).

Метод наложения.
В основе метода наложения лежит принцип суперпозиции, заключающийся в том, что ток в любой ветви электрической цепи можно рассчитать как алгебраическую сумму токов, вызываемых в ней от каждого источника в отдельности. Ток от отдельно взятого источника называется частным. При расчете частного тока все остальные источники ЭДС заменяются короткозамкнутыми перемычками, а ветви с источниками тока размыкаются. Поскольку в этом случае в рассматриваемых цепях остается только по одному источнику, расчеты производят не решением системы уравнений, а последовательным упрощением цепей путем использования правил для последовательного и параллельного соединения элементов, преобразования звезды в треугольник или треугольника в эквивалентную звезду и т. д.
Напомним основные правила и закономерности эквивалентного преобразования схем.
1. Эквивалентное сопротивление цепи, состоящей из последовательно соединенных сопротивлений, равно сумме этих сопротивлений. Падения напряжений на этих сопротивлениях прямо пропорционально этим сопротивлениям.
2. Эквивалентная проводимость цепи, состоящей из параллельно соединенных сопротивлений, равна сумме проводимостей этих сопротивлений. Протекающие через сопротивления токи прямо пропорциональны их проводимостям или обратно пропорциональны их сопротивлениям.
3. Звезду сопротивлений можно преобразовать в эквивалентный треугольник сопротивлений, как это показано на рис. 4, и наоборот.
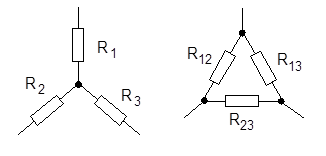
Рис. 4 Эквивалентные звезда и треугольник сопротивлений.
Формулы преобразования звезды сопротивлений в эквивалентный треугольник сопротивлений имеют вид:
 (8)
(8)
Для обратного преобразования можно использовать следующие выражения:
 (9)
(9)
Во всех случаях преобразования замена одних схем на другие, им эквивалентные, не должна привести к изменению токов или напряжений на участках цепи, не подвергшихся преобразованию.
Для расчета нашей схемы методом наложения на первом этапе исключим из нее все источники кроме E 1, а затем упростим ее. Все стадии упрощения приведены на рис. 5.
При эквивалентном преобразовании схемы (А) к схеме (Б) звезду сопротивлений r 3 R 3 R 5 преобразуем в треугольник сопротивлений R 1bc R 1bd R 1cd. Далее при преобразовании к схеме (В) учтем, что сопротивления R H и R 1cd, а также сопротивления r 2 R 4 и R 1bd соединены параллельно. Аналогичным образом осуществим переход к схемам (Г) и (Д).
Таким образом, к источнику E 1 оказываются подключенными последовательно соединенные сопротивления r1 и R ab. Отсюда ток
J 11 = E 1 / (r 1+ Rab) (10)
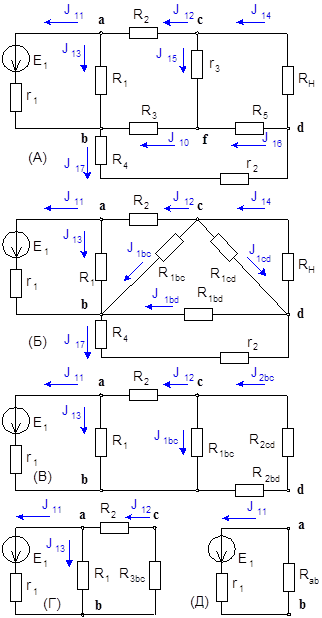
Рис. 5. Последовательное эквивалентное упрощение схемы.
Для определения значения токов J 12 и J 13 перейдем к схеме (Г) и учтем, что параллельно соединенные сопротивления образуют делитель тока. Следовательно:
 ;
;  (11)
(11)
Анализируя схему (В), не трудно заметить, что сопротивления R 1bc и R 2bd R 2cdтак же образуют делитель тока. Соответственно
 ;
; 
На основе анализа схем (А) и (Б), найдем токи
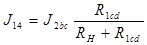 ;
; 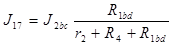 (12)
(12)
 ;
;  ;
;  (13)
(13)
Таким же образом, сначала упростив схему, определяются частные токи от источников Е 2 и Е 3.
После этого действительные токи в ветвях находят путем векторного, т.е. с учетом знаков, суммирования частных токов:
 (14)
(14)
Правильность расчетов, как обычно, проверяется с помощью проверки энергетического баланса мощностей.