Целью данного задания является научиться применять закон Ома при расчетах электрических цепей переменного тока. При выполнении задания необходимо уметь пользоваться различными формами записи комплексных величин, описывающих электрическую цепь, а также применять эти записи для вычисления токов, падений напряжений на отдельных элементах электрической цепи и построении векторных диаграмм.
В соответствии с вариантом индивидуального задания необходимо рассчитать параметры электрической цепи, представленной на рис. 7. Выполнение задания подразумевает определение номинальных значений элементов схемы, а также добротности реактивных элементов. Кроме того, необходимо рассчитать значения токов во всех ветвях электрической цепи и падение напряжения на всех ее элементах, вычислить действующие значения всех токов и приложенного к электрической цепи напряжения, построить векторную диаграмму и найти фазовый сдвиг между входным током и приложенным к электрической цепи напряжением.
Рис. 7. Схема электрической цепи переменного тока.
Предположим, что имеются следующие исходные данные к расчету:
| U | Z 1 | Z 2 | Z 3 | |||||
| f, Гц | Um, B | Ф, о | R1, Ом | X1, Ом | R2, Ом | X2, Ом | R3, Ом | X3, Ом |
| -40 |
Для определения реальных компонент электрической цепи учтем знаки при мнимых составляющих комплексных сопротивлений: если знак положительный, то сопротивление имеет индуктивный характер, если знак отрицательный, то сопротивление имеет емкостной характер. В нашем случае комплексные сопротивления Z 1 и Z 3 имеют индуктивный, а Z 2 - емкостной характер. Следовательно, нашу схему следует преобразовать к виду:
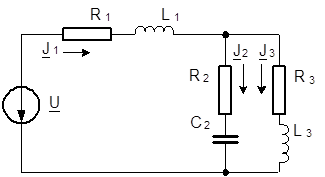
Рис. 8. Принципиальная схема разветвленной электрической цепи переменного тока.
Номинальные значения индуктивности и емкости определяются с помощью выражений:
; 
(17)
Для определения добротности элементов следует воспользоваться выражением:
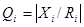(18)
Результаты вычислений номинальных значений элементов для выбранного варианта задания приведены в таблице:
| Z 1 | Z 2 | Z 3 | ||||||
| R1, Ом | L1, мГн | Q1 | R2, Ом | С2, мкФ | Q2 | R3, Ом | L3, мГн | Q3 |
| 0,5 | 3,33 | 0,2 |
Для определения токов в цепи следует воспользоваться законами Ома и Кирхгофа, но с учетом того, что все входящие величины являются комплексными.
Существует три формы записи комплексного числа. В алгебраической форме комплексное число А представляют в виде алгебраической суммы двух составляющих – вещественной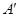 
и мнимой 
:
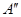(19)
где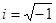 
обозначает мнимую единицу.
Число А можно изобразить в виде вектора на комплексной плоскости, у которой горизонтальная ось совпадает с осью вещественных составляющих, а вертикальная ось совпадает с осью мнимых составляющих комплексных чисел. По отношению к горизонтальной оси вектор А будет направлен под углом Ф. Положительное значение угла отсчитывается по часовой, отрицательное – против часовой стрелки.
Геометрическое рассмотрение вектора А на комплексной плоскости приводит к тригонометрической и экспоненциальной формам записи комплексного числа:
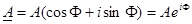(20)
где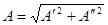 
- модуль, 
- фаза (аргумент) комплексного числа А.
Алгебраическую форму записи удобно применять при сложении и вычитании, а экспоненциальную – при умножении и делении комплексных чисел.
Вернемся к рассмотрению схемы, изображенной на рис. 7.
Сопротивление участка цепи с параллельно соединенными элементами Z 2 и Z 3 равно:
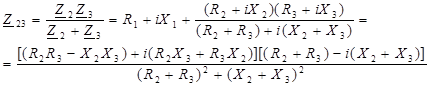Общее сопротивление цепи Z 0, подключенное к источнику U:
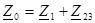(21)
Тогда токи в цепи будут равны:
; 
; 
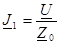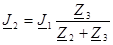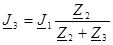(22)
Отсюда можно найти падения напряжения на отдельных элементах схемы:
; 
; 
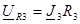(23)
; 
; 
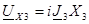(24)
Результаты численных расчетов приведены в таблице:
| параметр |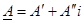 
| модуль А | Ф, о |
| U, B | -60-104i | -120 | |
| Z 0, Ом | 70+15i | ||
| J 1, A | -1,125-1,25i | 1,68 | -132 |
| J 2, A | 0,138-0,94i | 0.95 | -81,6 |
| J 3, A | -1,263-0,31i | 1,30 | -166 |
| U R1, B | -54-60i | 80,8 | -132 |
| U X1, B | 30-27i | 40,4 | -42 |
| U R2, B | 1.66-11,3i | 11,4 | -81,6 |
| U X2, B | -37,7-5,54i | 38,1 | -171 |
| U R3, B | -37,9-9,27i | 39,0 | -166 |
| U X3, B | 1,85-7,58i | 7,8 | -76 |
На основании расчетов построена векторная диаграмма (рис. 9).
Рис. 9. Векторная диаграмма напряжений и токов.
Следует обратить внимание, что при протекании тока через резисторы его направление совпадает с направлением вектора падения напряжения. На индуктивностях угол между током и напряжением составляет 900, а на емкости – минус 900.
Правильность расчетов следует проверить путем проверки выполнения баланса мощностей:
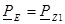(25)
Для нашей схемы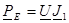 
, 
.
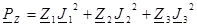Для определения действующих значений необходимо вспомнить, что действующим значением переменного тока называется такой постоянный ток, который за такое же время и на таком же сопротивлении выделяет такую же энергию, которая выделяется данным переменным током. Для гармонического тока действующие значения численно равны произведению амплитудных значений на постоянный коэффициент равный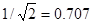 
.
Варианты индивидуального задания №1.
| № | E1, В | r1, Ом | E2, В | r2, Ом | E3, В | r3, Ом | R1, Ом | R2, Ом | R3, Ом | R4, Ом | R5, Ом | RH, Ом |
| 3, | ||||||||||||
Варианты индивидуального задания №2.
| № | U | Z 1 | Z 2 | Z 3 | |||||
| f, Гц | Um, B | Ф, о | X1, Ом | X1, Ом | R1, Ом | X1, Ом | R1, Ом | X1, Ом | |
| -7 | -18 | ||||||||
| -24 | -6 | ||||||||
| -9 | -20 | ||||||||
| -30 | |||||||||
| -27 | -7 | ||||||||
| -40 | |||||||||
| -36 | -9 | ||||||||
| -30 | -12 | ||||||||
| -27 | |||||||||
| -24 | |||||||||
| -36 | |||||||||
| -48 | |||||||||
| -27 | |||||||||
| -40 | |||||||||
| -36 | |||||||||
| -48 | -12 | ||||||||
| -18 | |||||||||
| -6 | -24 | ||||||||
| -20 | |||||||||
| -48 | |||||||||
| -18 | -7 | ||||||||
| -40 | -6 | ||||||||
| -20 | -9 | ||||||||
| -12 | -30 | ||||||||
| -7 | -16 | ||||||||
| -20 | -11 | ||||||||
| -12 | -30 |
Рекомендуемая литература.
1. Грошев И.В. Практикум по основам электроники. Часть I. Электрические цепи в режиме постоянного тока. – М.: Изд-во РУДН, 2003. – 62 с.
2. Евдокимов Ф.Е. Теоретические основы электротехники. – М.: Высшая школа, 2001. – 495 с.