Предмет инженерной графики.
Метод проекций.
3.Основные инвариантные свойства.
Свойства проекций плоских углов. Теорема о проецировании прямого угла.
Эпюр Монжа. Метод координат. Ортогональные проекции точки.
Приемы построения третьей проекции точки.
Начертательная геометрия (далее по тексту сокращение – НГ) представляет собой раздел геометрии, в котором пространственные формы предметов и их геометрические свойства изучаются при помощи изображений на плоскости, т.е. чертежей. Требования к чертежу:
1. Обратимость – по нему точно возможно воспроизвести форму и размеры изображаемого предмета.
2. Простота его графического выполнения.
3. Графические построения должны давать достаточно точные решения.
Содержание курса начертательной геометрии:
1. Изучение способов построения изображений (чертежей) пространственных фигур на плоскости.
2. Изучение способов решения на чертеже задач, связанных с геометрическими образами и их пространственным взаимным расположением.
3. Развитие пространственного мышления, т.е. по плоскому изображению образа мысленно уметь представить себе их объемную форму и взаимное расположение.
Геометрические образы – это точка, линия, поверхность, плоскость. При этом в НГ рассматриваются линии, а не часть пространства ими ограниченные (например, окружность, а не круг) и поверхности, не имеющие толщины и оснований, а не геометрические тела.
Метод проекций.
Основным методом НГ является проекционный метод, т.е. построение изображения геометрического образа на плоскости методом проецирования (отображения), от латинского слова (projecere = бросать вперед).
Метод проецирования заключается в том, что луч света, выходя из источника света (глаза) S, дает на плоскости отображение геометрического образа – точки. Источник света точку S, не принадлежащую плоскости, назовем центром проекций. Направление луча света SA назовем проецирующим лучом, плоскость П – плоскостью проекций, отображение А1 – проекцией точки.
 Рис.1
Рис.1
Лекция1-2
Существуют следующие проекционные модели:
- Центральное проецирование (перспектива - perspicere -смотреть сквозь).
- Параллельное проецирование.
- Ортогональное проецирование. Модель эпюра Монжа (эпюр- чертеж).
- Аксонометрическая модель.
Центральное проецирование – общий случай проецирования, при котором проецирующие лучи выходят из одной точки - центра проецирования S. Для построения проекции через точку А проводят проецирующий луч из центра проецирования S через точку А до пересечения с плоскостью проекций П (рис.2). Определение: Точка пересечения проецирующего луча SA с плоскостью проекций называется центральной проекцией точки А. Прямые, плоскости и конические поверхности, принадлежащие центру проецирования называются проецирующими (рис.3,4).
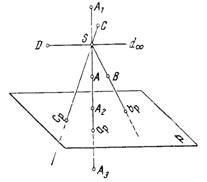 Рис.2
Рис.2

Рис.3 Рис.4
Но данный аппарат построения не дает обратимости чертежа, т.е. по одной проекции точки А нельзя восстановить положение самой точки в пространстве.

Рис.5
Чтобы чертеж стал обратимым, дополним аппарат вторым центром проецирования S2, получим вторую проекцию точки А. Отсюда важный вывод: две проекции точки однозначно определяют положение точки А в пространстве (рис.5).
Центральное проецирование дает достаточно большую наглядность, т.к. соответствует зрительному восприятию человека (глазу), но недостатком является сложность в определении размеров изображений. Используется преимущественно в архитектурно- строительных чертежах.
Лекция1-3
Параллельное проецирование – частный случай центрального, когда S центр проецирования удален в бесконечность, при этом проецирующие лучи становятся параллельны между собой. При этой системе проецирования необходимо задать плоскость проекций и направление проецирования, не параллельное этой плоскости (рис.6,7). Система является удобной при изображении объектов относительно небольших размеров, но не обладает наглядностью центральной проекции, особенно при изображении объектов большого протяжения, как, например, зданий, мостов и т.д.

Рис.6 Рис.7
Ортогональное проецирование. Параллельная проекция называется ортогональной (прямоугольной), если направление проектирования S перпендикулярно к плоскости проекций П. Для построения обратимых чертежей, аппарат дополняется второй плоскостью проекций, перпендикулярной к первой, и вторым ортогонально сопряженным направлением проецирования, и называется комплексным чертежом или методом Монжа. Метод прост в выполнении и дает большую точность графического решения задач, т.к. обеспечивает возможность точного определения изображений по чертежу. Недостаток – малая наглядность изображений.
3.Основные инвариантные свойства.
1.Точка проецируется в точку (рис.2). Проецирующий луч всегда пересекает плоскость только в одной точке, например, точки A,C,B (рис.2). Исключение: если высота точки равна высоте центра проецирования S, то центральная проекция точки будет бесконечно удаленной точкой – называемой несобственной точкой. В этом случае проецирующий луч будет параллелен плоскости проекций, например, точка D (рис.2).
2.Прямая проецируется в прямую. Прямая АВ и центр проецирования S (рис.6) образуют плоскость, которая пересекаясь с плоскость проекций П по прямой. Исключение: если направление проецирующего луча совпадает с самой прямой, то проекцией прямой будет точка. Например, A1A2=AS, то проекцией прямой будет точка ap. Точки А1 и A2 называются конкурирующими в отношении видимости к плоскости П. Видимой будет точка, находящаяся ближе к наблюдателю, т.е. точка A1(рис.2).
3. Если точка принадлежит прямой, то проекция точки принадлежит проекции прямой., например, точка N на AB (рис.6).
Параллельное проецирование сохраняет свойства центрального и обладает дополнительными свойствами:
4.Если прямые параллельны в пространстве, то их проекции параллельны, например, прямая AB параллельна CD (рис.7).
Лекция1-4
5.Отношение отрезков прямой равно отношению проекций этих отрезков, например, точка N делит отрезок AB и его проекцию в заданном отношении (рис.6).
6.Отношение отрезков параллельных прямых равно отношению проекций этих отрезков.
7.Проекця геометрического образа по величине и форме не изменяется при параллельном переносе плоскости проекций.
Ортогональному проецированию, помимо перечисленных выше, принадлежит еще одно свойство:
8. Проекция отрезка не может быть больше самого отрезка, например, отрезки AB и CD (рис.6).
4.Свойства проекций плоских углов. Теорема о проецировании прямого угла.
Из выше перечисленных свойств можно перейти к важной теореме, далее часто используемой в ортогональном проецировании.


Рис.8 Рис.9
«Если одна из сторон прямого угла параллельна плоскости проекций, а вторая не перпендикулярна ей, то прямой угол проецируется на плоскость проекций без искажения». (Запомнить!)
Доказательство:
Пусть сторона АВ прямого угла ВАС параллельна плоскости проекций, например (рис.8). Спроектируем угол ВАС ортогонально на плоскость П и докажем, что угол В1А1С1 прямой. АВ параллельна П. АВ и ее проекция А1В1 лежат в одной проецирующей плоскостиАВВ1А1, из чего следует, что АВ и А1В1 - параллельные прямые. На рис.9.
прямая АА1 перпендикулярна П, а значит АА1 перпендикулярнаА1В1 и АВ перпендикулярна АА1. Таким образом, прямая АВ перпендикулярна к двум прямым АА1 АС1,следовательно она перпендикулярна и к плоскости САА1. Но тогда А1В1 также перпендикулярна к плоскости САА1. Поэтому прямая А1В1 перпендикулярна к прямой А1С1, то есть угол В1А1С1- прямой. Естественно теперь задать вопрос об изменении величины произвольного угла при его ортогональном проецировании. Легко можно доказать, что проекции острого и тупого углов могут равняться проектируемому углу не только при условии параллельности плоскости угла, а, следовательно, и его сторон, плоскости проекций.
5.Эпюр Монжа. Метод координат. Ортогональные проекции.
Точку прямоугольно проецируем на три взаимно-перпендикулярные плоскости проекций:
0 – начало координат;
0X – горизонтальная ось (ось абсцисс); 0У – фронтальная ось (ось ординат) и 0Z –профильная ось (ось аппликат).
Координатные плоскости:
П1(или H)= (xoy)- горизонтальная плоскость проекций.;
П2(или V)= (xoz) – фронтальная плоскость проекций;
П3(илиW)= (yoz) – профильная плоскость проекций.
Лекция1-5



 z
z
 | |||
 | |||
П2
 А″ Аz
А″ Аz











 П3
П3
А″′

 А
А
Аx О





 x
x
П1 А′ Аy




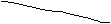
 y Рис.10
y Рис.10
АА1,АА2,АА3 – проецирующие лучи;
И соответственно:
А′ – горизонтальная проекция точки А;
А′″ ″ – фронтальная проекция точки А;
А′″ – профильная проекция точки А;
Координаты точки А – это ее расстояние до плоскостей проекций и будут иметь следующие значения:
А А′= А″Ах= Аz0= А′″Ау – высота точки ( координата z);
АА″ = А′Ах=Ау0= А′″Аz – глубина точки (координата у);
АА′″ = Ах0= А′Ау= А″Аz – широта точки (координата х).
Но пользоваться пространственной системой сложно, поэтому ее приводят к плоскому чертежу, который называется комплексным чертежом (Рис.9). Для этого совмещаем плоскость проекций П1 с плоскостью П2 путем вращения П1 вокруг оси в направлении, указанном на рисунке 11, так чтобы передняя полуплоскость П1 опустилась вниз и совместилась с нижней полуплоскостью П2, задняя полуплоскость поднялась вверх и совместилась с верхней полуплоскостью П2; и соответственно вращаем П3 вправо до совмещения с правой полуплоскостью П2. Получаем комплексный чертеж точки А:
 |
 А″ А′″
А″ А′″ 


 х Ах Ау
х Ах Ау 
 y
y
 А′ Ау k0
А′ Ау k0
 у
у
Рис.11
Множество горизонтальных проекций всех точек пространства называется полем горизонтальных проекций - соответствующая проекция фигуры называется – видом сверху; а множество фронтальных проекций всех точек пространства называется полем фронтальных проекций - соответствующая проекция фигуры называется – видом спереди или главным видом. Аналогично, множество профильных проекций всех точек пространства называется полем профильных проекций - соответствующая проекция фигуры называется – видом слева.
Лекция1-6
Для комплексного чертежа обязательно: А′А″, А′ Ау, Ау А′″,А″ А′″– линии связи всегда перпендикулярны к соответствующим осям проекций. Биссектриса правого нижнего угла является геометрическим местом вершин ломаных линий связи и называется постоянной прямой комплексного чертежа или постоянной эпюра Монжа k0 (рис.11).
Заметим, что плоскости проекций делят пространство на восемь октантов. Нумерация актантов показана на рис ниже.

Рис.12
Приемы построения третьей проекции точки.
Построение точки А по данным координатам(Ах,Ау, Аz) производится следующим образом: пользуясь единицей длины, строим отрезок 0Ах,равный координате ха, затем А′Ах, равный уа, параллельно оси У, и отрезок АхА″,равный za, параллельно оси Z. Проекции точки определяются координатами:
А′ (ха, уа); А″ (ха,zа); А′″ (yа,zа).
Видно, что любые две проекции точки однозначно определяют положение точки в пространстве, т.к. содержат все три координаты. Поэтому для задания точки достаточно задать любые две ее проекции и по двум данным легко построить третью недостающую. Для этого существуют следующие приемы:
1. воспользоваться постоянной чертежа ко (рис 13);
2. с помощью дуги окружности с центром в точке начала координат О (рис 14);
3. с помощью прямой уа-уа, проведенной под углом 45 градусов (рис 14);
4. использовать более простой и точный способ: глубина точки проецируется без искажения на плоскости П1 и П (Рис.15).


 z z z
z z z




Ад А′″ А″ А′″ А″ А′″
 | |||||
 |  | ||||







 x y x o y x o y
x y x o y x o y
А′ А′ А′
k0
Рис.13 Рис.14 Рис.15
Лекция1-7
Иногда для решения задач не требуются конкретные координаты точек, а важно взаимное расположение геометрических образов. Тогда не проводят оси координат и чертеж называется безосным (рис 16).
 |
А″ А′″
А′
Рис.16
Точка может находиться не только в первом октанте. Для того чтобы определить положение точки в любом октанте, устанавливаются знаки координат. Для решения задач поможет следующая таблица:
| Октанты | |||||||||||||||||
| Координаты | |||||||||||||||||
| Х | + | + | + | + | - | - | - | - | |||||||||
| У | + | - | - | + | + | - | - | + | |||||||||
| Z | + | + | - | - | + | + | - | - | |||||||||