Банковский, или коммерческий, учет (учет векселей) заключается в том, что банк до наступления срока платежа по векселю или другому платежному обязательству покупает его у владельца (являгощегося кредитором) по цене ниже той суммы, которая должна быть выплачена по нему в конце срока, т.е. приобретает (учитываст) его с дисконтом.
для расчета процентов при учете векселей применяется учетная ставка, которая обозначается символом (1. По определению, простая годовая учетная ставка находится по формуле:
(8)
Размер дисконта или учета, удерживаемого банком, равен
D = Snd. (9)
Тогда векселедержатель получит сумму, равную
Р- S D = S Snd=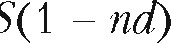 
= (t/k)d). (10)
Множитель (1 пф называется ДИСКОНТНЫМ лшоэк:итеием. Срок
п измеряет период времени от момента учета векселя до даты его погашения в годах. Дисконтирование по учетной ставке производится чаще всего при условии, что год равен 360 дням 
Пример 5. Через 90 дней предприятие должно получить по векселю 1 000 000 рублей. Банк приобрел этот вексель с дисконтом. Банк учел вексель по учетной ставке 20 0/0 годовых (год равен 360 дням) 
Определить дисконт D и полученную предприятием сумму Р.
Известно.
S = 1 000 000 руб, п = 90 дней, (1 = 0,20, или 2096.
Найти: 1) =? Р = 9
Решение
1-й вариант. Вычисления по формулам с помощью подручных вычислительных средств.
Для вычисления дисконта воспользуемся формулой 
D Snd 1 000 
50 000 руб 
По формуле (10) рассчитаем сумму, которую предприятие полу-
чит в результате учета векселя:
1 000 000 - 50 000 = 950 000 руб 
2-й вариант. Вычисления в Excel выполнены по формулам (9) и (10). Общий вид листа с расчетными формулами и результатами расчетов приведен на рис. 8.
| НЗ |
Рис. 8. Результаты вычислений дисконта D и суммы Р, полученной предприятием при учете векселя в среде Excel
|
|
(в ячейку НЗ введена формула: =В2*СЗ*В4)
Вычисления с помощью встроенных функций Excel 
Специальные функции в Excel для выполнения расчетов по операциям банковского и коммерческого учета с простыми учетными ставками не предусмотрены.
Сложные проценты
Сложные проценты применяются в долгосрочных финансовокредитных операциях (сроком более одного года), если проценты не выплачиваются периодически, сразу после их начисления за прошедший интервал времени, а присоединяются к сумме долга. Присоединение начисленных процентов к сумме, которая служила базой для их определения, называют капитализацией процентов.
2.1. Наращение по сложным процентам с постоянной ставкой
Пусть первоначальная сумма долга равна Р, тогда через один год сумма долга с присоединенными процентами составит Р(1 + i), через 2 года — Р(1 + + i) + через п лет Р(1 + i) 't. Таким образом, получаем формулу наращения для сложных процентов:
(11)
где S — наращенная сумма; i — годовая ставка сложных процентов; п срок ссуды;
(1 + i) 'i — множитель наращения.
На практике обычно используют дискретные проценты (проценты, начисляемые за одинаковые интервалы времени: год, полугодие, квартал) 
[> ЈЈримср 6. В кредитном договоре па сумму 1 000 000 руб. и сроком па 4 года зафиксирована ставка сложных ПРОЦСПТОВ, равная 20 0 0 ГОДОВЫХ.
Определить наращенную сумму.
Известно:
1 000 000 руб, п = 4 года; i = 0,20, или 20 0 0 
Найти: S = 
Решение
1-й вариант. Вычисления с помощью подручных вычислительных средств произведем по формуле (1 1)•
S = + = 1 000 000.(1 + = 2 073 600 руб 
2-й вариант. Для выполнения расчетов по формулам воспользуемся функцией СТЕПЕНЬ (находится в категории «Математические»). Данная функция возвращает результат возведения в степень (рис. 9) 
|
|
НЗ
| с | Н | |||||||||
| Дано 000 000 руб 4 года 0,20 | Решение
Расчет наращенной суммы, по истечении 4-х лет
| |||||||||
| Найти |
а
Возвращает рзуљтат
|
«Ило (1484) аопе в стане. Степа• стегв•м, в ттсрую
|
2,076 
б
Рис. 9. Результаты расчета наращенной суммы S (а) и вид диалогового окна СТЕПЕНЬ с введенными данными (б)
(в ячейку НЗ введена формула 
Для выполнения расчетов по формулам воспользуемся функцией БС (находится в категории «Финансовые»). Данная функция возвращает результат возведения в степень (рис. 10) 
-Ю 1.1)
| с Дано 1 000 000 руб 4 года 0,20 | Решение
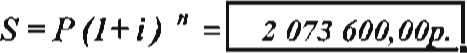 Расчет наращенной суммы, по функции БС
| |
14 Найти 
| ||
а
2:07 Возврацает будущую стато:ть ь—естиј.и на
ТИП О 1, гм В ...аге переда (щ) игм же воце геррда (Р отсутстзе
|
(рамк св.“) платехзђ и
20730 
Рис. 10. Результаты расчета наращенной суммы S по функции
БС (а) и вид диалогового окна БС с введенными данными (б)
(в ячейку Н 12 введена формула: = 
Синтаксис функции БС (ставка; кпер; плт; пс; тип) 
Ее аргументами являются.
ставка — процентная ставка за период; кпер — общее число периодов платежей по аннуитету;
п.лт — выплата, производимая в каждый период; ее значение неизмеппо в течение всего периода выплат. Обычно п.лт состоит из
ОСНОВНОГО платежа и платежа по процентам, но не включает других Н&ЛОГОВ и сборов. Если аргумент опущен, должно быть указано значение аргумента нс;
|
|
пс — приведенная к текущему моменту стоимость или общая сумма, которая на текущий момент равноценна ряду будущих платежей. Если аргумент пс опущен, то он полагается равным 0. В этом случае должно быть указано значение аргумента плт; тип — число 0 или 1, обозначающее, когда должна производиться выплата (0 — в конце периода; 1 — в начале периода). Если аргумент «тип» опущен, то он полагается равным 0. 