Если ставка СЛОЖНЫХ процентов МСПЯСТСЯ во времени, то формула наращения имеет следующий вил:
| действующих |
| в |
| соответ- |
7. В финансовом договоре зафиксирована переменная 
ставка сложных процентов, определяемая как годовых плюс маржа 1 0 0 0 в первые два гола, 8 0 0 в третий гол, в четвертый гол.
Определить ВС.ЛИЧИЩУ МПО>КИТС.ЛЯ за М гола.
Известно:
0,20, ИЛИ 20 0 0,
— 0,10, или 1 0 0 0,
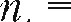2 гола;
| Решение |
1-й вариант. Вычисления с ПОМОЩЬЮ подручных вычислительПЫХ средств произвелем по формуле (12):
= (1 + 
+ 0,25) ОМ 
для выполнения расчетов по формулам воспользуемся функцией ПРОИЗВЕД (находится в категории «Математические»). Данная функция возвращает результат возведения в степень (рис. 1 1).
а
Аргфуеще»
Ч-слоз: «по:,ЧСР02,'... от до 33 «ел,
|
«ел, в зде теста.
б
Рис. 11. Результаты расчета множителя наращения (а) и вид диалогового окна ПРОИЗВЕД с введенными данными (б)
(в ячейку Ј4 введена формула:
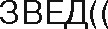1 +ВЗ+ОЗ) Л 1 
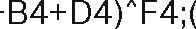1 +В5+О5) Л Г-5))
3-й вариант. Предварительно следует подготовить исходные данные по форме, представленной на рис. 12, а. Для выполнения рас четов следует воспользоваться функцией БЗРАСПГIС (находится в категории «Финансовые»). Данная функция возвращает будущее
значение основного капитала после начисления сложных процентов с переменной ставкой (рис. 12). Поскольку здесь рассчитывается множитель наращения, то в качестве первоначальной суммы ВВОДИТСЯ 1 (рис. 12, б).
а
Аргументы
Гфич-т 
2,704
Возвращает будущее мачење «мтапа 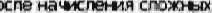 граде-;тое,
План - это  гртвчю.ъв гр:ментеы tr•:«.
 2,704 
|
б
Рис. 12. Результаты расчета множителя наращения (а) и вид диалогового окна БЗРАСПИС с введенными данными (б)
|
|
(в ячейку К 13 введена формула: = БЗРАСПИС(1; G12:G15))
Синтаксис функции БЗРАСПИС (первичное; план) 
Аргументы функции. первичное — действительное число, задающее первоначальную стоимость инвестиции; план — массив значений, содержащих процентные ставки.
Напомним, что для вычисления будущей стоимости с постоянной ставкой используется функция БС. 
Номинальная и эффективная ставки процентов
Номинальная ставка
Пусть годовая ставка сложных процентов равна у, а число периодов начисления в году равно т. При каждом начислении проценты капитализируются, т.е. добавляются к сумме с начисленными в предыдущем периоде процентами. Каждый раз проценты начисляют по ставке ] т. Ставка] называется номинальной. Начисление процентов по номинальной ставке ПРОИЗВОДИТСЯ по формуле:
где N— число периодов начисления (У = может быть и дробным ЧИСЛОМ).
Пример 8. Ссуда в размере 20 000 000 руб. предоставлена на 28 месяцев. Проценты сложные, ставка — 18 0 0 годовых. Проценты начисляются ежеквартально.
Вычислить наращенную сумму по 
срока.
Известно:
Р- 20 000 000 руб,
п 28 месяцев = 28 12 лет,
Решение
1-й вариант. ВЫЧИС№НИЯ с помощью подручных ВЫЧИСЛИТеЛЬПЫХ средств произведем по формуле (13).
Всего за п лет имеем
= 4. (28/12) = 28/3
периодов начислений при ежеквартальном (т = 4) начислении процентов в году. По формуле (13) находим.
S = 20 000 000.(1 + 0,18 = ЗО 161 206,25 руб 
2-й вариант. Для выполнения расчетов воспользуемся функцией СТЕПЕНЬ (из категории «Математические»). Данная функция возвращает результат возведения в степень (рис. 13)
3-й вариант. Вычисления с помощью встроенных функций 
Excel. Для выполнения расчетов воспользуемся функцией БС (из категории «Финансовые»). Результаты расчета приведены на
|
|
Рис. 13. Результаты расчета наращенной суммы S по номинальной ставке
| 2 з | в о Дано Р = 20 000 руб 'f тп = 4 * (28/12) = 9.3 периодов 0.18 или 1890 | Решение
Расчет наращенной суммы S по номинальной ставке с использованием финансовой нкчии БС
| |
| 5 Найти |
т) =
| с |
Рис. 14. Результаты расчета наращенной суммы S по номинальной ставке с использованием финансовой функции БС
(в ячейку 1-44 введена формула: 
2.3.2. Эффективная ставка
При финансовом анализе широко используется понятие эффективной ставки. Чем выше эффективная ставка финансовой операции, тем при прочих равных условиях она выгоднее кредитору.
Эффективная ставка показывает, какая годовая ставка сложных процентов дает тот же финансовый результат, что и т-разовое наращение в году по ставкеј/т.
Если проценты капитализируются т раз в году, каждый раз со ставкой ј/т, то, по определению, можно записать равенство для соответствующих множителей наращения.
тп (14) где i, ] — эффективная и поминальная ставки.
Связь между эффективной и номинальной ставками выражается соотношением
| Э |
Пример 9. Вычислить эффективную ставку процента, если банк начисляет проценты ежеквартально, исходя из номинальной ставки 16 0 0 годовых.
Известно:
| О |
Решение
1-й вариант. Вычисления с помощью подручных вычислитель-
П ЫХ средств производим по формуле (15)•
1 = 0,170, ИЛИ 17,0 0 0.
|
|
2-й вариант. Расчет эффективной ставки выполним в Excel по формуле (15), результаты расчета представлены на рис. 15.
| з |
Рис. 15. Результаты расчета эффективной ставки в среде Excel
(в ячейку НЗ введена формула: =(1+ВЗ/В2) Л В2-1)
3-й вариант. Расчет эффективной ставки выполним в среде Excel с использованием функции ЭФФЕКТ (из категории «Финансовые»). Данная функция возвращает эффективную (фактическую) процентную ставку при заданной номинальной процентной ставке и количестве периодов, за которые начисляются сложные проценты (рис. 16)
Синтаксис функции ЭФФЕКТ (номинальная ставка; кол_периолов).
Аргументы функции.
номинальная ставка — значение номинальной процентной ставки; кол периодов — количество периодов начисления.
Обратная зависимость между номинальной и эффективной ставками выражена следующей формулой.
| ||
| з | в с Дано | Решение
Расчет эффективной ставки по номинальной ставке — (1 4 ] / т)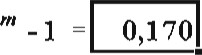 
|
| Найти — 9 |
а
Аргументы
Кол_пвр • »то  год.
| |
б
Рис. 16. Результаты расчета эффективной ставки (а) и вид диалогового окна ЭФФЕКТ с введенными данными (б)
(в ячейку НЗ введена формула: =ЭФФЕКТ(ВЗ;В2))
Пример 10. Определить, какой должна быть номинальная ставка при ежеквартальном начислении процентов, чтобы обеспечить эффективную ставку 12 % годовых.
Известно:
i = 0,12, или 12 0 0.
Найти:ј 
Решение
1-й вариант. Вычисления с помощью подручных вычислительных средств произведем по формуле (16)•
| .7) |
2-й вариант. Для ВЫПОЛНСПИЯ расчетов по формулам в среде Excel воспользуемся математической функцией СТЕПЕНЬ (рис. 17).
Рис. 17. Результаты расчета эффективной ставки в среде Excel
(в ячейку НЗ введена формула: 
1+B3;1/B2)- 1))
3-й вариант. Для выполнения расчетов номинальной ставки воспользуемся функцией НОМИНАЛ (из категории «Финансовые»). Лапная функция возвращает номинальную годичную ставку при залаппой эффективной ставке и числе периодов, за которые начис.ЛЯЮТСЯ проценты. Результаты расчета приведены на рис. 18.
| |||||
| з | в с Дано 0,12 | Решение
Расчет номинальной ставки по эффективной
| |||
а
фугаем
дргумеглть•
83 = 6,12 0,114949379 Воз»а.цает нт•ънањнро годи!.нро гдентнро ст Кодјер - это
|
схтавляацих год.
з.чение-0ј11495 
б
Рис. 18. Результаты расчета номинальной ставки (а) и вид диалогового окна НОМИНАЛ с введенными данными (б)
(в ячейку НЗ введена формула: =НОМИНАЛ(ВЗ;В2))
функции НОМИНАЛ (эффект ставка; кол пер). Аргументы функции.
эффект ставка — значение эффективной процентной ставки, 
кол пер — количество периодов начисления.
2.4. Учет (дисконтирование) по сложной
Ставке процентов
Математический учет
В этом случае решается задача, обратная наращению по сложным процентам. Запишем формулу S = Р(1 + О п для наращения по сложной ставке с начислением процентов один раз в году и перепишем ее относительно Р:
где дробь
является учетным, или дисконтным, множителем.
Пример 11. Через 5 лет предприятию будет выплачена сумма 1 000 000 руб 
Определить ее современную стоимость при условии, что применяется ставка сложных процентов 14 0 0 годовых.
Известно:
| руб |
| , |
Решение
1-й вариант. Вычисления с помощью подручных вычислительных средств выполним по формуле (17):
1 000 000/(1 + 519 368,66 руб
2-й вариант. Для выполпепия расчетов в Excel по формулам воспользуемся математической функцией CTEllEl ll). l la рис. 1.9 привелены два варианта ИСПОЛЬЗОВТШЯ лапной функции.
3-й вариант. для ВЫПО.ЛП(МИЯ расчетов по ВСТРОСППЫМ в Excel функциям ВОСПОЛЬЗ.УСМСЯ финансовой функцией l lC (рис. 20). Лаппая функция возвращает привелеппуо стоимость инвестиции при УСЛОВИИ периодических РТШЫ,Х по величине платежей и ПОСТОЯМпой процентной ставки.
а
б
Рис. 19. Результаты расчета современной стоимости в среде Excel (в ячейку НЗ введена формула: а) =ВЗ/СТЕПЕНЬ(1+В4;В2);
D -ВЗ 1)
| -ПС(В4 с | о | |||||||||
| Дано 5 лет S = 1 000 000 руб 0,14 | Решение
Расчет современной стоимости по финансовой функции ПС
| |||||||||
| 2 з | ||||||||||
| Найти | ||||||||||
а аргумен•ьз
5с будущая ть игм одла-с, НУЖНО досмеь госге 
 
|
б
Рис. 20. Результаты расчета современной стоимости (а) и вид диалогового окна ПС с введенными данными (б)
(в ячейку НЗ введена формула: =ПС(В4;В2;0;-ВЗ; 1))
Синтаксис функции ПС (ставка; кпер; плт; бс; тип). Аргументы функции.
ставка — значение процентной ставки за один период; кпер — количество периодов начисления; плт — величина платежа (можно опускать, когда аргумент принимает нулевое значение); бс необязательный аргумент, задает будущую стоимость или остаток средств после последней выплаты; тип — необязательный аргумент (принимает значение 0, когда выплаты производятся в конце периода, значение 1, когда выплаты производятся в начале периода). 
начислении процентов т раз в году используется формула:
пт гле
(2пт — 
дисконтный множитель.
Величину Р, полученную дисконтированием S, называют совреМиТОЙ, или текущей, стоимостью, или привеДенной величиной S
Суммы Р и S эквивалентны в том смысле, что платеж в сумме S через п лет равноценен сумме Р, выплачиваемой в настоящий моМ(МТ. Здесь разность D = S - Р называется Дисконтом.