для определения срока простой ренты при платежах по схеме постпџмераш)о используется следующая формула:
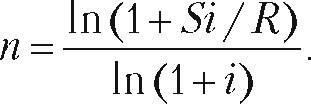
[> Пример 22. l la момент окончания финансового соглашения заемщик должен выплатить 30 000 000 руб. 
размером 5 000 000 руб поступают ежегодно в конце гола с 
по СЛОЖНОй процентной ставке 1 5 0 0 ГОДОВЫХ.
Определить срок простой ренты постпџмераш)о.
Известно:
R = 5 000 000 руб),
S = ЗО 000 000 руб),
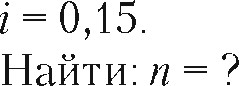
Решение
1-и вариант. Вычисления по формулам с помощью подручных вычислительных средств. По формуле (32) находим.
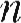= ln(1 + ЗО 000 000-0,15/5 000 
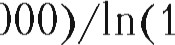+ 0,15) = 4,59 года 
2-й вариант. Для выполнения расчетов по формулам в среде Excel в строку формул вводим формулу (32) и для вычисления степени используем функцию LN (рис. 41) 
Рис. 41. Результаты расчета в Excel срока ренты п постнумерандо по известной наращенной сумме S
(в ячейку Н4 введена формула: =LN(
1+В4))
3-й вариант. Вычисления с помощью встроенных функций Excel 
Выполним расчеты с использованием функции КПЕР (категория «Финансовые»), рис. 42. 
| с | о | Е | р: | ||||||||||
| Дано 5 000 000 года 30 000 000 руб. i= 0,15 | Решение
Расчет срока простой ренты постнумерандо по функции КПЕР | ||||||||||||
Найти 
| |||||||||||||
годаРис. 42. Результаты расчета в Excel срока ренты п с использованием функции ПЛТ
(в ячейку 1-44 введена функция: =КПЕР(В4;-В2;;ВЗ))
Если рентные п.лШ'с>ки осуществляются по схеме пренум,еранДо, то определение срока п простой ренты производится по формуле:
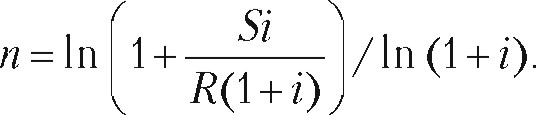(33)
Пример 23. для условий примера 22 определить срок простых рент пренум,еранДо.
Известно:
R = 5 000 000 руб,
S = ЗО 000 000 руб,
Найти: п
Решение
1-й вариант. ВЫЧИСЛеНИЯ по формулам с помощью подручных вычислительных средств. По формуле (33) находим:
|
|
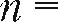ln (1 + ЗО 000 
000 000.(1 + 0,15)) ln (1 + 0,15) 
4,1 /1 гола.
2-й вариант. Для выполнения расчетов по формулам в среде
Excel в строку формул вводим формулу (33) и для ВЫЧИС№НГШ стеИСП И используем логарифмическую функцию LN (категория «Математические»), рис. 43.
| |||
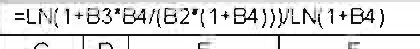
| В 2 R- 5 000 000 руб. з S = ЗО 000 000 руб. 4 0,15 | Решение
андо по формуле
4,14 года | ||
| 5 Найти | |||
Рис. 43. Результаты расчета в Excel срока ренты п пренумерандо по известной наращенной сумме S
(в ячейку Н4 введена формула: =LN(
1+B4)))/LN(1+В4))
3-й вариант. Вычисления с помощью встроенных функций Excel. Выполним расчеты с использованием функции КПЕР (категория «Финансовые»), рис. 44. 
ЛЕР\В4.-В2..ВЗ.1
| с О Е | Н | |||||||
| 2 з | Дано R = 5 000 000 руб S = ЗО 000 руб. 0,15 | Решение
Расчет срока простой ренты пренумерандо по функции КПЕР года | ||||||
| 5 Найти | ||||||||
Рис. 44. Результаты расчета в Excel срока простой ренты п по известной будущей стоимости S с использованием функции КПЕР
(в ячейку Н4 введена функция: =КПЕР(В4;-В2;;ВЗ;1))
Определение срока простой ренты п при известной современной стоимости ренты А
Срок простой ренты при платежах по схеме постнумеранДо определяется по следующей формуле:
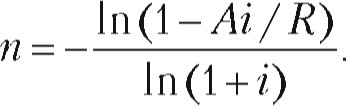(34)
Пример 24. Организация взяла кредит в размере 30 000 000 руб 
с условием погашения ежегодными платежами по 6 000 000 руб. в конце года (постнумерандо) и начислением по сложной процентной ставке 15 0 0 годовых.
Определить срок простой ренты.
Известно.
А = ЗО 000 000 руб,
R = 6 000 000 руб,
Найти: п 
Решение
1-й вариант. Вычисления по формулам с помощью подручных вычислительных средств. По формуле (34) находим.
|
|
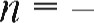Л (1 - ЗО 000 000-0,15/6 000 000)/ln (1 + 0,15) = 9,92 года 
2-й вариант. Для выполнения расчетов по формулам в среде Excel в строку формул вводим формулу (34) и для вычисления степени используем функцию LN (категория «Математические»), рис. 45.
Рис. 45. Результаты расчета в Excel срока ренты п постнумерандо по известной современной стоимости д простой ренты
(в ячейку Н4 введена формула: =-LN(1-B2*B4/B3)/LN((1+В4))
3-й вариант. Вычисления с помощью встроенных функций Excel. Выполним расчеты с использованием функции КПЕР (категория «Финансовые»), рис. 46. 
| 2 з | А = ЗО 000 000 руб. R = 6 000 000 руб. i= 0,15 | (З
Решение
Расчет срока простой ренты постнумерандо по функџии КПЕР года
| |
Найти п =?
|
Рис. 46. Результаты расчета в Excel срока простой ренты п постнумерандо с использованием функции КПЕР
(в ячейку Н4 введена формула:=КПЕР(В4;ВЗ;-В2))
В случае, когда реализуется рента пренџмеранДо, срок ренты рассчитывается по формуле:
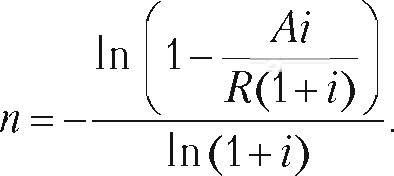
[> Пример 25. Для условий примера 24 определить сроки простых репт пренумеранДо.
Известно:
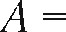ЗО 000 000 руб, R = 6 000 000 руб,
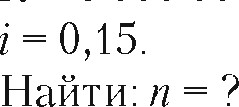
Решение
1-й вариант. ВЫЧИСЛеНИЯ по формулам с помощью подручных вычислительных средств. По формуле (35) находим.
ln (1 ЗО 000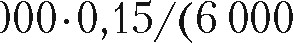 
000.(1 + 0,15)) Л (1 + 0,15) = 
7,56 гола.
2-й вариант. Для выполнения расчетов по формулам в среде 
Excel в строку формул вводим формулу (35) и для вычисления степепи используем функцию логарифмирования LN (категория «Математические»), рис. 47 
Рис. 47. Результаты расчета в Excel срока ренты п пренумерандо по известной современной стоимости д простой ренты
|
|
(в ячейку Н4 введена формула: =-LN(1-В2*В4/(ВЗ(1+B4)))/LN(1+В4))
3-й вариант. Вычисления с помощью встроенных функций Excel 
Выполним расчеты с использованием функции КПЕР (категория «Финансовые»), рис. 48. 
Рис. 48. Результаты расчета в Excel срока простой ренты п пренумерандо с использованием функции КПЕР
(в ячейку 1-14 введена формула: =КПЕР(В4;ВЗ;-В2;;1))
3.5. Определение величины процентной ставки
Простой ренты
При заключении финансовых сделок важно знать их доходность, которая определяется процентной ставкой ренты за один период начисления. При этом считается, что известны следующие значеПИЯ: отдельныЙ платеж К, срок займа п и наращенная сумма S (или современная стоимость А). Процентная ставка ренты находится в результате решения нелинейного уравнения.
В Excel данная задача решается с ПОМОЩЬЮ финансовой функции стлвкл.
Синтаксис функции СТАВКА(кпер; пл; пс; бс; тип; предположение).
Аргументами данной функции являются:
кпер — общее число периодов платежей по аннуитету; плт — регулярный платеж (один раз в период), величина которого остается постоянной в течение всего срока аннуитета. Обычно плт состоит из платежа основной суммы и платежа процентов, но не включает других сборов или налогов. Если аргумент опущен, должно быть указано значение аргумента бс; пс — приведенная к текущему моменту стоимость или общая сумма, которая на текущий момент равноценна ряду будущих платежей; бс требуемое значение будущей стоимости или остатка средств после последней выплаты. Если аргумент бс опущен, то он полагается равным 0 (например, бс для займа равно 0); тип — число 0 или 1, обозначающее, когда должна производиться выплата (0 или опущен в конце периода, 1 в начале периода); предположение — указывается предполагаемая величина ставки
(от 0 до 1). По умолчанию аргумент принимает значение равное 0, 1 (или 10 0 0) 
Если последовательные результаты функции СТАВКА не сходятся с точностью 0,0000001 после 20 итераций, то появляется сообщение 06 ошибке #ЧИСЛО
Пример 26. Для того чтобы по истечении двух лет получить 5 000 000 руб., предприятие первоначально может ЖЛОЖИТЬ 500 000 руб. с фиксированным ежемесячным платежом 100 000 руб 
Определить годовые процентные ставки простых рент постнумерандо и пренумеранДо.
Известно.
= 5 000 000 руб.,
R = 100 000 руб., Р = 500 000 руб, п = 2 года. Найти: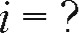 
Решение
1-й вариант. Вычисления по формулам с помощью подручных вычислительных средств. Решение задачи по формулам затрудне-
но, поскольку требуется реализация итерационного процесса в расчетах.
2-й вариант. Выполнение расчетов по формулам в среде Excel затруднено тем, что необходимо реализовать итерационный алгоритм.
3-й вариант. Вычисления с помощью встроенных функций Excel. Выполним расчеты с использованием функции СТАВКА (категория «Финансовые»), рис. 49.
| |||
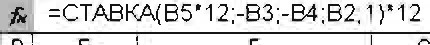
| с о Е но Решение | |||
| S = | руб. руб. года | 1. Расчет годовой процентной ставки простой ренты постнумеранд о по функции 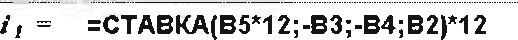 СТАВКА
2. Расчет годовой процентной ставки простой ренты пренумерандо по функции СТАВКА
| |
| Б В | Найт |
а
| |||
с
дано
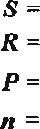 5 000 000 руб
100 000 руб. 500 000 руб. з года
| D Е
Решение
1. Расчет годовой процентной ставки про постнумерандо по функции СТАВКА
2. Расчет годовой процентной ставки простой ренты пренумерандо по функции СТАВКА
| ||
| Найти | |||
б
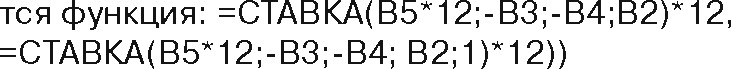Рис. 49. Расчетные формулы (а) и результаты расчета (б) в Excel годовой ставки простой ренты постнумерандо и пренумерандо с использованием функции СТАВКА (в ячейке Н4 используется функция: в ячейке НВ:
Особенностью использования функции СТАВКА является то, что опа вычисляет процентную ставку не для года, а для периода (в данном случае для месяца), поэтому полученный результат умножается на 12 — количество месяцев в году 
3.6. Современная (приведенная) величина
Финансовой ренты
3.6.1. Современная величина Д обычной годовой
Финансовой ренты
Если член годовой ренты равен R, процентная ставка i, срок ренты п и проценты начисляются один раз в конце года, тогда дисконтированная величина первого платежа будет равна:
R= Rv,
1 -4- 
1 где = дисконтный множитель.
Приведенная к началу ренты величина второго платежа равна Rv2 и т.д. В итоге приведенные величины образуют геометрическую прогрессию: Rv, Rv2 Rv3 Rv't, сумма которой равна:
(36)
где ап 
коэффициент приведения ренты, который
зависит только от двух параметров — срока ренты п и процентной ставки i.
Пример 27. В течение трех лет на расчетный счет в конце каждого года (р = 1) поступает по 10 млн руб. Ежегодное ДИСКОНТИРОвание производится по сложной процентной ставке 10 0 0 годовых. Определить современную стоимость ренты.
Известны:
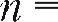З года,
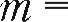1, R - 10 000 000 руб, р 1,
Решение
1-й вариант. Вычисления по формуле (36) с помощью подручных вычислительных средств:
А = 10 000 00041 (1 + 
= 24 868 519,91 руб 
2-й вариант. Для выполнения расчетов по формулам в среде Excel в строку формул вводится формула (36) с использованием математической функции СТЕПЕНЬ (рис. 50) 
| F•i5 |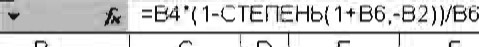 
| ||
| 2 з | с
Дано з года 1
10 000 000 руб 
0.10
| О Е
Решение
Расчет современной стоимости ренты по формуле
А = [(141 
| |
| Найти |
Рис. 50. Результаты расчета современной величины обычной годовой финансовой ренты в Excel
(в ячейку Н5 введена формула: 1 -СТЕПЕНЬ(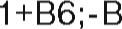
3-й вариант. Для выполнения расчетов воспользуемся функцией ПС (категория «Финансовые»). Данная функция возвращает приведенную стоимость инвестиции (рис. 51). 
Рис. 51. Результаты расчета современной стоимости ренты д с использованием финансовой функции ПС
(в ячейку Н5 введена формула: = ПС(В6;В2;-В4))
3.6.2. Современная величина р-срочной финансовой ренты с произвольными значениями 1 1 (р * т)
Данный вариант является общим для нахождения современной величины ренты, когда р и т могут принимать произвольные значения. Здесь используется формула:
(37)
которая включает все возможные частные случаи 
Пример 28. В течение трех лет на расчетный счет в конце каждого квартала поступают платежи (р = 4) равными долями из расчета 10 млн руб. в год, т.е. по 10/4 МЛН руб. в квартал. Ежемесячное дисконтирование (т 12) производится по сложной ставке 10 00 годовых.
Определить современную стоимость ренты.
Известно: п З года; т = 12,
R = 10 000 000 руб,
Найти: А =?
Решение
1-й вариант. Вычисления по формуле (37) с помощью подручных вычислительных средств.
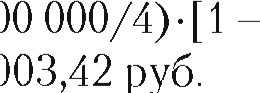А = (10 000 000 (1 +0,10 12 У- 1 2-3)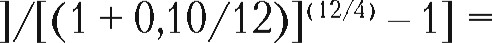 
25 612
2-й вариант. Для ВЫПО.ЛПСПИЯ расчетов по формулам в среде Excel в строку формул вводится формула (37) с использованием математической функции СТЕПЕНЬ (рис. 52).
2
Расчет современной стоимости ренты по формуле
Рис. 52. Результаты расчета современной стоимости р-срочной финансовой ренты в Excel
(в ячейку Н4 введена формула:
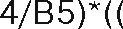1 -СТЕПЕНЬ(1 
3-й вариант. ВЫЧИСЛеНИЯ с помощью встроенных функций Excel. для решения этой задачи в среде Excel финансовую функцию подобрать не удалось.