МЕТОДИЧЕСКИЕ УКАЗАНИЯ
По выполнению практических занятий по дисциплине
АСТРОНОМИЯ
Для обучающихся
По профессии 46.01.03 Делопроизводитель
Разработчик: Меренкова О.Ю.
с. Обшаровка 2017г.
ПОЯСНИТЕЛЬНАЯ ЗАПИСКА
Методические указания по выполнению практических занятий составлены в соответствии с рабочей программой дисциплины Астрономия для оказания помощи обучающимся по профессии СПО 46.01.03 Делопроизводитель в организации и успешном выполнении практических занятий по предмету Астрономия.
Содержание методических указаний соответствует структуре учебника Астрономия 11 класс, Б.А. Воронцов-Вельяминов, Е.К. Страут - М.: Просвещение, 2014г.
При изучении истории на проведение практических занятий отводится 16 часов, по два часа на каждое практическое занятие.
Практическое занятие:
1) одна из форм учебного занятия, целью которого является формирование у студента практических навыков и умений;
2) это одна из форм учебной работы, которая ориентирована на закрепление изученного теоретического материала, его более глубокое усвоение и формирование умения применять теоретические знания в практических, прикладных целях. Особое внимание на практических занятиях уделяется выработке учебных или профессиональных навыков. Такие навыки формируются в процессе выполнения конкретных заданий — упражнений, задач и т. п. — под руководством и контролем преподавателя.
Астрономия – древняя и прекрасная наука о Вселенной, безграничном и постоянно меняющемся мире, включающем в себя огромную область, доступную современным наблюдениям. Это и Солнце с планетами, и звезды, и галактики, и многочисленные системы, образуемые ими, и разреженная среда, в которой все они находятся.
|
|
За свою длительную историю астрономические наблюдения были необходимы и для определения продолжительности года, времени наступления того или иного сезона, и для установки системы счета времени, и для прокладывания курса кораблей в открытом море... Сегодня многие эти проблемы решаются техническими средствами. Но современная астрономия отнюдь не оторвана от жизни. Задачи, требующие наиболее высокой точности измерений, и в настоящее время решаются с привлечением новейших методов астрономии.
Понять природу наблюдаемых тел и явлений во Вселенной, их возникновение и развитие, дать объяснения их свойствам, используя знания естественных наук, физико-математическое и философское образование - задача курса.
Данные методические указания будут способствовать закреплению у обучающихся теоретических знаний и выработке практических навыков в определении местоположения, времени и физических характеристик небесных объектов. Они разработаны в соответствии с рабочей программой учебной дисциплины Астрономия и предназначены для оказания помощи при выполнении практических занятий обучающимися.
В результате освоения содержания учебной дисциплины Астрономия обучающийся должен достичь следующих результатов:
- сформированность представлений о строении Солнечной системы, эволюции звезд и Вселенной, пространственно-временных масштабах Вселенной;
- понимание сущности наблюдаемых во Вселенной явлений;
- владение основополагающими астрономическими понятиями, теориями, законами и закономерностями, уверенное пользование астрономической терминологией и символикой;
|
|
- сформированность представлений о значении астрономии в практической деятельности человека и дальнейшем научно-техническом развитии;
- осознание роли отечественной науки в освоении и использовании космического пространства и развитии международного сотрудничества в этой области.
КРИТЕРИИ ОЦЕНИВАНИЯ ПРАКТИЧЕСКИХ ЗАНЯТИЙ
Критериями оценки результатов работы обучающегося являются:
- уровень освоения учебного материала;
- умение использовать теоретические знания при выполнении практических занятий;
- четкость и структурированность изложения ответа;
- оформление материала в соответствии с требованиями.
Оценки за выполнение практических занятий выставляются по пятибалльной системе и учитываются как показатели текущей успеваемости обучающихся.
ПЕРЕЧЕНЬ ПРАКТИЧЕСКИХ ЗАНЯТИЙ
| П/п | Раздел | Название практических занятий | Количество часов | |
| Раздел 2.Основы практической астрономии | Практическое занятие №1Изучениеиспользования в работе звездных атласов, подвижной карты звездного неба, астрономических календарей и справочников. | |||
| Практическое занятие №2Изучение систем счета времени. | ||||
| Раздел 3. Законы движения небесных тел. | Практическое занятие №3Изучение закономерностей законов Кеплера и конфигурации планет. | |||
| Раздел 4. Солнечная система. | Практическое занятие №4Изучение видимого годового движения Солнца и его последствий. | |||
| Практическое занятие №5Изучение карты и рельефа Луны и больших спутников планет. | ||||
| Раздел 5. Методы астрономических исследований | Практическое занятие №6Изучение небольших оптических телескопов. | |||
| Раздел 6. Звезды | Практическое занятие №7Определение положений и условий видимости планет. | |||
| Практическое занятие №8Изучение солнечной активности и общего излучения Солнца. | ||||
| итого | ||||
|
|
Практическое занятие № 1 (2 часа)
ИЗУЧЕНИЕ ИСПОЛЬЗОВАНИЯ В РАБОТЕ ЗВЕЗДНЫХ АТЛАСОВ,ПОДВИЖНОЙ КАРТЫЗВЕЗДНОГО НЕБА,АСТРОНОМИЧЕСКИХ КАЛЕНДАРЕЙ И СПРАВОЧНИКОВ
Цель работы:ознакомление с содержанием звездных атласов и их использованием при изучении звездного неба. Использование подвижной карты при изучении звездного неба. Ознакомление с содержанием и использованием астрономических календарей и справочников.
Оборудование:атлас звездного неба А. А. Михайлова, Астрономический календарь (постоянная и переменная части), подвижная карта звездного неба, школьный астрономический календарь. Электронные справочники и базы данных.
Вопросы к допуску:
1.Понятие созвездия.
2.Устройство и назначение подвижной карты звездного неба.
3.Астрономические календари.
Основные теоретические сведения
Звездные атласы служат пособием при изучении звездного неба и при вы- полнении научно-исследовательских работ по астрономии. На каждой карте атла- са изображен определенный участок звездного неба, спроектированный на плос- кость. Атлас звездного неба А. А. Михайлова состоит из 20 карт и содержит все звезды обоих полушарий до 6,5 звездной величины. Координаты звезд даны для эпохи 1950 года. К атласу прилагается общий каталог звезд, который содержит не только координаты звезд, но также их видимую звездную величину и тип спектра. Видимый блеск звезд различен и выражается в условных единицах, назы- ваемых звездными величинами (m). Наиболее яркие звезды считаются звездами нулевой видимой звездной величины (0m). Звезды, блеск которых приблизительно в 2,5 раза слабее блеска звезд 0m, считаются звездами первой видимой величины (1m). На пределе видимости невооруженным глазом находятся звезды 6-й видимой звездной величины (6m), которые слабее звезд 1-й видимой звездной величины в100 раз.
Поправка на прецессию. Вследствие возмущающего действия, оказываемо- го на вращение Земли Луной и Солнцем, ось вращения Земли совершает в про- странстве очень сложное движение. Она медленно описывает конус, оставаясь все время наклоненной к плоскости движения Земли под углом около 66°,5. Это
движение называется прецессионным, период его около 26 000 лет. Оно определя- ет среднее направление оси в пространстве в различные эпохи.
Вследствие изменения положения земной оси в пространстве из-за явления прецессии меняет свое положение ось мира и небесный экватор. Сетка экватори- альных координат, связанная с небесным экватором, медленно поворачивается в пространстве, изменяются экваториальные координаты звезд.
Чтобы определить координаты звезд в произвольный год, нужно к коорди- натам звезды, данным в каталоге на 1950 г., прибавить изменение координат вследствие прецессии за столько лет, сколько прошло с 1950 г. до данного года. Для этой цели служит таблица прецессии за 100 лет, имеющаяся в звездном ката- логе. Поправка по прямому восхождению на 100 лет Da100 находится по значению
a1950 и d1950; d1950 определяет нужную строку, a1950 нужный столбец. Поправка на данный год находится из соотношения:
Dan = Da100 . n/100,
где n — количество лет, прошедшее с 1950 года. Поправка по склонению на 100
лет находится по значению a1950. Дальнейшие операции аналогичны предыдущим.
Подвижная звездная карта служит пособием для общей ориентировки на небе. Пользуясь ею, можно решить целый ряд задач и, в частности, определить рас- положение созвездий относительно истинного горизонта. На карте изображены: сетка небесных экваториальных координат и основные созвездия, состоящие из сравнительно ярких звезд. Карта составлена в проекции, в которой небесные парал- лели изображаются концентрическими окружностями, а круги склонения — луча- ми, выходящими из северного полюса мира, расположенного в центре карты. Рядом с ним находится звезда a Малой Медведицы, называемая Полярной звездой.
Круги склонения проведены через 15 ° (1h) и оцифрованы в часах по одной из небесных параллелей вблизи внутреннего обреза карты. Небесный экватор и три небесных параллели в 30 ° оцифрованы в точках их пересечения с начальным кругом склонения (a = 0 h) и с диаметрально противоположным ему кругом скло- нения (a = 12h). Оцифровка кругов склонения и небесных параллелей позволяет грубо оценивать значения экваториальных координат небесных светил. Эксцен- трический овал, пересекающийся с небесным экватором в двух диаметрально про- тивоположных точках, изображает эклиптику.
Область карты, заключенная внутри небесного экватора, представляет се- верную небесную полусферу. По наружному обрезу карты, называемому лимбом дат, нанесены календарные числа и названия месяцев года. Накладной круг, при- лагаемый к карте, позволяет установить вид звездного неба для любого времени суток произвольного дня года. Для этого внешний обрез круга, называемый часо- вым лимбом, разделен на 24 часа, по числу часов в сутках.
Часовой лимб оцифрован в системе среднего времени. В накладном круге имеется вырез, положение которого определяется географической широтой места наблюдения. Контур овального выреза изображает истинный, или математиче- ский горизонт, на котором нанесены названия четырех его главных точек — точек
юга, запада, севера и востока. Прямая, соединяющая точки севера и юга, изобра- жает небесный меридиан. Положение зенита определяется точкой пересечения этой прямой с небесной параллелью, склонение которой равно широте места на- блюдения.
Подвижная карта звездного неба позволяет приближенно решать ряд задач практической астрономии. Например, чтобы определить вид звездного неба в не- который момент времени заданного дня года, нужно наложить накладной круг концентрично на звездную карту, чтобы штрих часового лимба, указывающий данный момент времени, совпал со штрихом заданной даты, а небесный меридиан всегда проходил через северный полюс мира. Тогда внутри овального выреза окажутся те звезды, которые в заданный момент времени видны над горизонтом.
Светила, которые окажутся на прямой, соединяющей точки севера и юга, проходят в данный момент через меридиан, т.е. кульминируют. В верхней куль- минации будут те светила, которые располагаются на этой прямой между север- ным полюсом мира и точкой юга. Те светила, которые располагаются на небесном меридиане между северным полюсом мира и точкой севера, находятся в данный момент в нижней кульминации.
С помощью подвижной карты звездного неба можно получить положение Солнца на любой день года. Для этого необходимо соединить прямой полюс мира со штрихом, отмечающим заданную дату месяца. Точка пересечения этой прямой с эклиптикой и будет местом нахождения на небе Солнца в данный день года.
Астрономические календари содержат сведения, необходимые для астро- номических наблюдений, их обработки и решения многих других задач. По со- держанию астрономические календари делятся на две группы. Первая содержит краткое изложение теоретических основ различных разделов астрономии, спра- вочные таблицы и сведения постоянного характера. К этой группе принадлежит “Астрономический календарь (постоянная часть) ВАГО”. Справочные сведения постоянного характера содержатся в “Справочнике любителя астрономии” П.Г. Куликовского, в различных каталогах и справочных таблицах. В последнее время появилось много электронных справочников, таблиц и баз данных.
К другой группе астрономических календарей относятся астрономические ежегодники, содержащие сведения об астрономических явлениях текущего года: “Астрономический календарь-ежегодник (переменная часть) ВАГО”, “Астроно- мический ежегодник”, “Авиационный астрономический ежегодник” и др. Суще- ствует много астрономических программ для ЭВМ, позволяющих находить раз- личную информацию о небесных явлениях в нужный момент времени.
Литература:
1. Астрономический календарь. Постоянная часть. М ., 1981.
2. Астрономический календарь ежегодник. Переменная часть. М.
3. Бакулин П.И ., Кононович Э.В ., Мороз В.И. Курс общей астрономии. М ., 1983.
4. Куликовский П.Г. Справочник любителя астрономии. М ., 1971.
Для получения зачета необходимо:
1. Уметь пользоваться звездным атласом.
2. Свободно владеть подвижной звездной картой при решении различных задач.
3. Уметь пользоваться астрономическими календарями и справочниками для нахождения необходимых сведений.
Образец заданий
1. По картам звездного атласа определить экваториальные координаты и видимую звездную величину двух наиболее ярких звезд в созвездии Кассиопеи.
2. Выписать названия ярких созвездий, по которым проходит Млечный Путь.
3. Найти на звездной карте созвездие Малого Пса.
По карте определить координаты a и d звезды Процион (a Малого Пса).
Найти эту звезду в общем каталоге звезд, определить точные координаты a и d,
звездную величину (mag) и тип спектра (sp).
4. Взять из общего каталога координаты звезды Дубхе и определить ее координаты на 2004 год, пользуясь таблицей прецессии за 100 лет.
5. Установить подвижную звездную карту на день и час занятий для Минска и ука- зать, какие созвездия будут в верхней и нижней кульминации.
6. В день 15 июля найти момент восхода, верхней кульминации и захода звезды Си- риус (a Большого Пса).
7. Определить день года, в который в 20h30m в верхней кульминации находится звезда Альдебаран.
8. По таблицам в “Астрономическом календаре” (постоянной части) найти названия и видимую звездную величину звезд, положения которых определяются экватори- альными координатами:
1. a = 46 °38¢1,”5 2. a = 151 °45¢37,”5
d = + 40 °51¢38” d = +12 °05¢24”
9. Из эфемерид Солнца и Луны найти моменты времени восхода и захода этих све- тил в пункте l = 0h, j = 56 °, азимуты точек их восхода и захода, найти моменты их верхней кульминации на текущий день.
10. Из эфемерид Луны выписать даты и моменты времени четырех основных ее фаз в текущем месяце.
11. Найти положение и моменты времени восхода и захода планеты Юпитер в дан- ный день.
Примеры выполнения некоторых заданий
4. Взять из общего каталога звезд атласа координаты (a и d) звезды Дубхе и опре - делить ее координаты на 2004 год, используя таблицу прецессии за 100 лет.
Итак, прежде всего необходимо найти примерные координаты данной звезды по звездной карте атласа для того, чтобы определить, в какой части общего каталога звезд искать заданную звезду.
Но сначала определим, какому созвездию принадлежит звезда Дубхе. Ответ на- ходится в таблице «Собственные имена звезд» атласа звездного неба А. А. Михайло- ва: a UMa. Сокращенное латинское название созвездия (Uma), найденное в данной таблице, можно расшифровать с помощью следующей таблицы «Названия созвез- дий»: Uma – Большая Медведица. Здесь же находим номера карт атласа, на которых частично изображена Большая Медведица. На 4-й карте находим a Uma. По верхней и нижней дуговым шкалам определяем прямое восхождение (a » 11h), а по левой и правой – склонение (d » 62°). В общем каталоге звезд (в этом же атласе) по прямому восхождению находим a Uma и уточняем коордитнаты (a1950 = 11h 0.7м; d1950 = 62°1¢). Данные координаты в общем каталоге звезд соответствуют равноденствию 1950 го- да. Поэтому, для уточнения их на заданный год необходимо найти разницу в годах между заданным и 1950-ым: Dt = 2004 – 1950 = 54 года и воспользоваться таблицей прецессии за 100 лет (в конце атласа). Данная таблица состоит из двух частей: “по прямому восхождению”, где содержатся приращения координат Da100, и “по склоне- нию”, где – приращения координат Dd100 за 100 лет. В таблице “по прямому восхож- дению” по координатам (a1950 = 11h 0.7м; d1950 = 62°1¢) находим соответствующее приращение: Da100 = 6.2m (4-й столбец, 8-я строка). В таблице “по склонению” по ко- ординате a1950 находим соответствующее приращение: Dd 100 = -32 ¢ (4-я строка сни- зу). Но нам необходимо приращение координат не за 100 лет, а за Dt = 54 года, т.е.
Da54 и Dd54, значения которых находим по формулам:
Dan = (Da100 / 100) ´ n и Ddn = (Dd100 / 100) ´ n.
Таким образом, Da54 = 3.35m и Dd54 = - 17.3 ¢, а координаты на заданный год a2004 =
a1950 + Da54 = 11h 0.7m + 3.35m = 11h 3.42m; а d2004 = 62°1 ¢ – 17.3 ¢ = 61°43.7 ¢.
Практическое занятие № 2 (2 часа)
ИЗУЧЕНИЕ СИСТЕМ СЧЕТА ВРЕМЕНИ
Цель работы:изучение различных систем счета времени.
Оборудование:модель небесной сферы, астрономический календарь
(постоянная и переменная части), подвижная звездная карта.
Вопросы к допуску:
1. Понятие звездного времени.
2. Среднее и истинное солнечное время.
3. Уравнение времени.
4. Связь местного времени с географической долготой.
Основные теоретические сведения
Измерение времени основано на наблюдениях суточного вращения не- бесного свода и годичного движения Солнца, т.е. на вращении Земли вокруг оси и на обращении Земли вокруг Солнца.
Вращение Земли вокруг оси происходит почти равномерно, с периодом, равным периоду вращения небесного свода. Поэтому по углу поворота Земли от некоторого начального положения можно судить о протекшем времени. За начальное положение Земли принимается момент прохождения плоскости зем- ного меридиана места наблюдения через избранную точку на небе, или, что од- но и то же, момент верхней кульминации этой точки на данном меридиане.
Продолжительность основной единицы времени, называемой сутками, зависит от избранной точки на небе. В астрономии за такие точки принимают- ся:
— точка весеннего равноденствия (звездное время),
— центр видимого диска Солнца (истинное Солнце, истинное солнечное вре- мя),
— среднее Солнце — фиктивная точка, положение которой на небе может быть вычислено теоретически для любого момента времени (среднее солнечное вре- мя).
Для измерения длинных промежутков времени служит тропический год, основанный на движении Земли вокруг Солнца.
Тропический год — промежуток времени между двумя последовательны- ми прохождениями центра истинного Солнца через точку весеннего равноден- ствия. Содержит 365,2422 средних солнечных суток.
Из-за медленного движения точки весеннего равноденствия навстречу Солнцу, вызванного прецессией, относительно звезд Солнце оказывается в той же точке неба через промежуток времени на 20 мин. 24 с. больший, чем тропи- ческий год. Он называется звездным годом и содержит 365,2564 средних сол- нечных суток.
Звездное время. Промежуток времени между двумя последовательными одноименными кульминациями точки весеннего равноденствия на одном и том же географическом меридиане называется звездными сутками.
За начало звездных суток на данном меридиане принимают момент верхней кульминации точки весеннего равноденствия.
Время, протекшее от верхней кульминации точки † до любого другого ее положения, выраженное в долях звездных суток, называется звездным вре - менем S.
Угол, на который Земля повернется от момента верхней кульминации точки весеннего равноденствия до какого-нибудь другого момента, равен часо- вому углу точки † в этот момент.
S = t†.
Практически для установления начала звездных суток или звездного времени в какой-то момент надо измерить часовой угол t какого-либо светила М, прямое восхождение которого известно. Тогда звездное время:
S = a + t,
где t = (Qm, a = (†m, а t† = (Q† = S.
Звездное время в любой момент равно прямому восхождению какого- либо светила плюс его часовой угол. В момент верхней кульминации светила его часовой угол t = 0, тогда S = a.
Звездное время для наблюдателей, находящихся на разных меридианах, будет разным. Разность звездного времени в двух пунктах земной поверхности в один и тот же физический момент равна разности географических долгот этих пунктов.
S2 - S1 = l2 - l1.
Истинное солнечное время. Промежуток времени между двумя после- довательными одноименными кульминациями Солнца (центра солнечного дис- ка) на одном и том же географическом меридиане называется истинными сол - нечными сутками. За начало истинных солнечных суток на данном меридиане принимают момент нижней кульминации Солнца (истинная полночь).
Время, протекшее от нижней кульминации Солнца до любого другого его положения, выраженное в долях истинных солнечных суток называется истин - ным солнечным временем Тс.
Истинное солнечное время Тс на данном меридиане в любой момент:
Т h
где tс – часовой угол Солнца.
с = tс + 12,
Истинные солнечные сутки имеют различную продолжительность, так как:
1. Солнце движется не по небесному экватору, а по эклиптике, наклоненной к экватору под углом 23°26¢.
2. Движение Солнца по эклиптике неравномерно.
Среднее солнечное время. Чтобы получить сутки постоянной продолжи- тельности и в то же время связанные с движением Солнца, в астрономии введе- ны понятия двух фиктивных точек — среднего эклиптического и среднего эк- ваториального Cолнца.
Среднее эклиптическое Солнце равномерно движется по эклиптике со сред- ней скоростью Солнца.
Среднее экваториальное Солнце равномерно движется по экватору с посто- янной скоростью среднего эклиптического Солнца и одновременно с ним про- ходит точку весеннего равноденствия.
Промежуток времени между двумя последовательными одноименными кульминациями среднего экваториального Солнца на одном и том же геогра- фическом меридиане называется средними солнечными сутками.
Продолжительность средних солнечных суток равна среднему значению продолжительности истинных солнечных суток за год.
За начало средних солнечных суток на данном меридиане принимают мо- мент нижней кульминации среднего экваториального Солнца (средняя пол - ночь).
Время, протекшее от нижней кульминации среднего экваториального Солн- ца до любого другого его положения, выраженное в долях средних солнечных суток, называется средним солнечным временем Тm.
|
Тm = tm + 12,
где tm– часовой угол Солнца.
Разность между средним и истинным солнечным временем в один и тот же момент называется уравнением времени h.
h = Tm - Tc = tm - tc = ac - am,
где t – часовой угол, а a — прямое восхождение.
Отсюда следует
Tm = Tc + h = tc +12h + h.
Уравнение времени обращается в нуль около 15 апреля, 14 июля, 1 сен- тября и 24 декабря, и четыре раза в году принимает экстремальные значения, из них наиболее значительные около 11 февраля (h = +14m) и 2 ноября (h = -16m).
Уравнение времени публикуется в астрономических календарях - еже- годниках ВАГО для каждой средней полуночи на меридиане Гринвича. Если в календаре дан момент верхней кульминации центра истинного Солнца, то имея
в виду, что этот момент дан по среднему времени, и что в данный момент ис- тинное солнечное время равно 12h, получим уравнение:
h = Tm - 12h.
Всемирное время. Местное среднее солнечное время гринвичского ме- ридиана называется всемирным, или мировым временем Т0.
|
Tm = Т0 + l,
где lh – долгота данного пункта, выраженная в часовой мере (h).
Поясное время. Местных систем счета времени бесчисленное множество, как и меридианов.
В 1884 году была предложена поясная система счета среднего времени. Счет времени ведется только на 24 основных географических меридианах, рас- положенных друг от друга по долготе точно через 15°, приблизительно посере - дине каждого часового пояса. За основной меридиан нулевого пояса принят Гринвичский.
|
Тm- Tn
= l - nh,
h
Tn= Т0 + n
где nh– число целых часов, равное номеру часового пояса (долгота основного меридиана часового пояса).
Декретное время. В целях более рационального распределения электро- энергии, идущей на освещение предприятий и жилых домов, в летнее время вводят летнее время. В СССР 16.07.1930г. декретом правительства стрелки ча- сов перевели на 1 час вперед против поясного времени.
Литература:
1. Астрономический календарь. Постоянная часть. М ., 1981
2. Бакулин П.И ., Кононович Э.В ., Мороз В.И. Курс общей астрономии. М ., 1983
4. Куликовский П.Г. Справочник любителя астрономии. М ., 1971
Для получения зачета необходимо:
1. Уметь свободно ориентироваться в разных системах счета времени.
2. С помощью подвижной звездной карты уметь определить звездное время, зная в этот момент среднее местное время, а также уметь решать и обратную задачу.
3. Представить преподавателю оформленные вычисления, требуемые в задании.
Образец заданий
1. На модели небесной сферы показать взаимосвязь прямого восхождения и часового угла светила со звездным временем.
2. Найти звездное время в момент захода точки весеннего равноденствия.
3. Определить звездное время в Екатеринбурге и Минске, если в Бишкеке звездное время равно 2h40m25s.
4. Для того же момента времени в тех же городах вычислить часовые углы звезд Альдебаран и Спика, выразив их в угловой мере и в единицах времени.
5. По подвижной карте звездного неба определить приближенное значение звездного времени в среднюю полночь и средний полдень 25 февраля, 25 мая, 25 августа и 25 ноября.
6. По подвижной карте звездного неба определить для тех же дней приближен- ное значение среднего времени в момент 18h звездного времени.
7. Определить, с точностью до 1 минуты, момент верхней кульминации Солн- ца по звездному, истинному солнечному, среднему местному, поясному, декретному времени в Берлине 2 ноября. (l = 13°25¢).
8. В момент кульминации звезды Ригель (a = 5h13m) часы, идущие точно по звездному гринвичскому времени, показывают 15h9m; определить долготу данного места.
Примеры выполнения некоторых заданий
1. Определить, с точностью до 1 минуты, момент верхней кульминации Солнца по звездному, истинному солнечному, среднему местному, поясному времени в Берлине 2 ноября. (l = 13°25 ¢ ).
В данном случае удобнее начать с истинного солнечного времени Тс. т. к. Солнце в верхней кульминации, то по истинному солнечному времени будет полдень, т.е. Тс = 12h. Среднее солнечное время отличается от истинного сол- нечного на поправку «уравнение времени» (h = Т m - Тс), которая содержится в эфемеридах Солнца в астрономическом календаре-ежегоднике: h0(2) = - 16m. По- этому Т m = Тс + h = 12h 00m – 16m = 11h 44m. Поясное время Тп связано с местным средним солнечным Т m соотношением: Т m - Тп = lh - nh, где lh — географиче- ская долгота пункта, выраженная в часовой мере, а nh – номер часового пояса в часах. Откуда Тп = Т m - lh + nh. Но прежде необходимо перевести в часовую
меру lh, воспользовавшись таблицей перевода (АК, постоянная часть) или со- отношениями: 1h = 15°, 1m = 15¢, 1m = 15¢¢. Итак, lh = 0h 53m 40s. А поясное время Тп = 11h 44m - 0h 53m 40s + 1h = 11h 50m 20s. Звездное время S = a с + t с, где
a с – прямое восхождение Солнца, содержится в эфемеридах Солнца в астроно- мическом календаре-ежегоднике: a с = 14h 30m. А часовой угол Солнца в верх- ней кульминации t с = 0h. Поэтому звездное время S = a с = 14h 30m.
2. В момент верхней кульминации звезды Ригель (a = 5h13m) в некотором гео - графическом пункте часы, идущие точно по звездному гринвичскому време - ни, показывают 15h9m. Определить долготу данного пункта.
Звездное время на данном меридиане можно найти по координатам звезды: S= a + t. Звезда Ригель находится в верхней кульминации, значит ее часовой угол t = 0. Следовательно, в данном пункте S1 = a с = 5h13m. А по звездному гринвичскому времени в этот момент S0 = 15h9m. Но известно, что S0 - S1 = l0 -
l1, поэтому l1 = l0 - S0 + S1. Для Гринвича l0 = 0. Следовательно, l1 = 0 -
15h9m + 5h13m = - 9h56m. (Минус показывает, что отсчет долготы происходит к западу от гринвичского меридиана). Долготу можно записать и положительной, но для этого нужно добавить 24h. То есть, 24h - 9h56m = 14h4m и отсчет долготы происходит к западу от гринвичского меридиана.
Практическое занятие № 3 (2 часа)
ИЗУЧЕНИЕ ЗАКОНОВ КЕПЛЕРА И КОНФИГУРАЦИИ ПЛАНЕТ
Цель работы:изучение закономерностей в движении планет и вычисление их конфигураций с помощью модели Солнечной системы.
Оборудование:модель Солнечной системы, астрономический календарь
(постоянная часть), астрономический календарь-ежегодник.
Вопросы к допуску:
1. Формулировка законов Кеплера.
2. Эклиптическая система координат.
3. Конфигурации планет.
Основные теоретические сведения
Движение планет вокруг Солнца описывается законами Кеплера, которые были сформулированы Иоганном Кеплером так:
1. Все планеты движутся по эллипсам, в одном из фокусов которых ( общем для всех планет ) находится Солнце.
2. Радиус - вектор планеты в равные промежутки времени описывает равнове - ликие площади.
3. Квадраты сидерических периодов обращений планет вокруг Солнца пропор - циональны кубам больших полуосей их эллиптических орбит.
|
|
|
|
2 3
2 2
где Т1, Т2 — сидерические периоды обращений планет, а1, а2 — большие по- луоси их орбит.
Если большие полуоси орбит выражать в единицах среднего расстояния от Земли до Солнца (в а.е.), а периоды обращений в годах, то для Земли а = 1, Т
= 1, и период обращения любой планеты вокруг Солнца равен:
Т = Öа3.
Благодаря работам И. Ньютона получены обобщенные законы Кеплера, кото- рые в настоящее время имеют вид:
1. Под действием силы притяжения одно небесное тело движется в поле тя - готения другого небесного тела по одному из конических сечений — кругу, эллипсу, параболе или гиперболе.
Эта формулировка подходит для описания движения всех небесных тел: спут- ников, комет, двойных звезд и др.
2. Площадь, описанная радиусом вектором за единицу времени есть величина постоянная.
|
r const,
dt
где q — полярный угол (истинная аномалия).
3.
= a 1 3
|
|
где M и m — массы центрального тела и спутника, индексы 1 и 2 относятся к различным парам “тело-спутник”.
В данной работе предполагается проверка третьего закона Кеплера в пер- вом приближении, при этом можно считать орбиты планет круговыми и лежа- щими в одной плоскости.
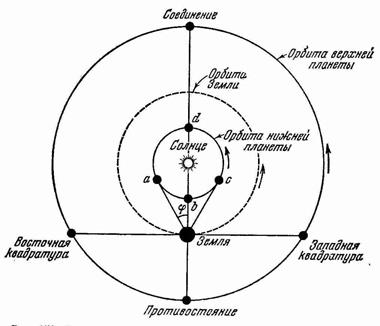При своём движении по орбитам планеты могут занимать различные поло- жения относительно Солнца и Земли. Эти положения на- зываются конфигурации. Конфигурации различаются для нижних и для верхних планет. Нижними являются планеты, находящиеся бли- же к Солнцу, чем Земля, верхними - те, которые дальше.
Для нижних планет выделяют конфигурации: нижнее и верхнее соедине-
ние с Солнцем, наибольшая западная и восточная элон- гации. Слово элонгация оз-
Рис .6 Конфигурации планет
начает удаление. Смысл двух элонгаций заключается в том, что если мы будем наблюдать нижние планеты с Земли, то они будут находиться на самом боль- шом угловом расстоянии от Солнца. Когда планета находится в соединении, то она с Земли не наблюдается, так как максимально сближается с Солнцем и те- ряется в его лучах.
Конфигурации для верхних планет несколько иные. Верхние планеты имеют соединение,