1. Дан одномерный массив. Написать функцию, определяющую минимальный, максимальный элементы массива и среднее арифметическое минимального и максимального элементов. Кроме того, программа должна иметь функцию ввода одномерного массива и функцию вывода.
2. 
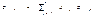Написать функцию перемножения матриц А размером nхm и В размером mхl. Элементы результирующей матрицы получить с помощью следующей формулы. Массивы должны быть динамическими.
3. Написать функции вычисления суммы элементов каждой строки матрицы А размером 6х6, определения наибольшего значения этих сумм.
4. Дана действительная матрица размера 6х9. Найти среднее арифметическое наибольшего и наименьшего значений ее элементов. Программа должна быть составлена с использованием функций.
5. В квадратной матрице размера mxn найти значение наибольшего по модулю элемента матрицы, а также определить индексы этого элемента. Предполагается, что такой элемент - единственный. Программа должна быть составлена с использованием функций.
6. В данной действительной квадратной матрице порядка N найти сумму элементов строки, в которой расположен элемент с наименьшим значением. Предполагается, что такой элемент единственный. Программа должна быть составлена с использованием функций.
7. В одномерном массиве, состоящем из n вещественных чисел, вычислить:
а) количество элементов массива, меньших С;
б) сумму положительных элементов, расположенных после первого положительного элемента.
Преобразовать массив таким образом, чтобы сначала располагались все элементы, целая часть которых лежит в интервале [a, b], а потом – все остальные.
Программа должна быть составлена с использованием функций.
|
|
Лабораторная работа 4
Перегрузка функций
Перегрузка функции - это определение двух или более функций с одним и тем же именем, но разным набором параметров. Работа перегруженных функций основана на различии списков параметров (на различии их типов и/или количестве), принимаемых функцией. При обращении к функции компилятор использует то определение функции, тип и количество параметров которой совпадают с типом и количеством параметров, передаваемых в функцию при обращении к ней.
Перегруженные функции не могут отличаться только типом возвращаемого значения.
Пример перегрузки функций, вычисляющих среднее арифметическое значение для двух целых чисел, для трех целых чисел, для двух действительных чисел и трех действительных чисел.
# include < iostream >
using namespace std;
double avg (int a, int b);
double avg (int a, int b, int c);
double avg (double a, double b);
double avg (double a, double b, double c);
int main()
{
int x, y, z;
cout << ” Enter 3 integers \n ”;
cin >> x >> y >> z;
cout << ” average value of 2 numbers = ” << avg (x, y);
cout << ” average value of 3 numbers = ” << avg (x, y, z);
double n, m, k;
cout << ” Enter 3 real numbers \n ”;
cin >> n >> m >> k;
cout << ” average value of 2 real numbers = ” << avg (n, m);
cout << ” average value of 3 real numbers = ” << avg (n, m, k);
return 0;
}
double avg (int a, int b) { return (a + b) / 2.0;}
double avg (int a, int b, int c) { return (a + b + c) / 3.0; }
double avg (double a, double b) { return (a + b) / 2; }
double avg (double a, double b, double c) {return (a + b + c) /3;}
Шаблоны функции
Шаблоны функции позволяют создавать функции, которые могут использовать аргументы различных типов. Большинство функций используют алгоритмы, которые могут работать с различными типами данных. Например, функция сортировки может сортировать символьные, вещественные и целочисленные массивы.
|
|
Использовать несколько определений идентичных функций, работающих с данными разного типа, не эффективно. В этом случае следует использовать шаблоны функции. При этом определение и прототип функции начинаются со строки template < class T >. Эта строка является префиксом шаблона и указывает компилятору, что следующее за ним определение функции является шаблоном, а Т - параметром типа. Слово class в этом случае обозначает тип. В качестве Т может быть указан любой тип.
Определение шаблонов функции на самом деле является большим набором количества определений функции. Каждый из этих определений получается замещением параметра типа Т именем соответствующего типа. Компилятор при обращении к функции сам создает ее определение на основе шаблона. Прежде, чем создавать шаблон функции, необходимо создать обыкновенную функцию, и только после ее отладки преобразовать в шаблон.
Пример: универсальная функция сортировки.
# include < iostream.h >
template < class T >
void sort (T a[ ], int size);
main () {
char c [ 8 ] = {‘ p ’, ’ r ’, ’ o ’, ’ g ’, ’ r ’, ’ a ’, ’ m ’, ’ \0 ’ };
sort (c, 8);
int A [ 5 ] = { 5, 10, 1, 4, 9 };
sort (A, 5);
double B [ 4 ] = { 3.2, 1.5, 9.8, 2.8 };
sort (B, 4);
return 0;
}
template < class T >
void sort (T a [ ], int size) {
int i, P;
T D;
for (p = 1; p <= size - 1; p ++)
for (i = 0; i < size - 1; i ++)
if (a [ i ] > a [ i + 1 ]) {
D = a [ i ];
a [ i ] = a [ i + 1 ];
a [ i +1] = D;
}
Рекурсивные функции
Программы, которые мы обсуждали до сих пор, в общем случае состояли из функций, которые вызывали какие-либо другие функции в строгой иерархической манере. В некоторых случаях полезно иметь функции, которые вызывают сами себя. Рекурсивная функция — это функция, которая вызывает сама себя либо непосредственно, либо косвенно с помощью другой функции.
|
|
Рекурсивная задача в общем случае разбивается на два этапа. Для решения задачи вызывается рекурсивная функция. Эта функция знает, как решать только простейшую часть задачи — так называемую базовую задачу (или несколько таких задач). Если эта функция вызывается для решения базовой задачи, она просто возвращает результат. Если функция вызывается для решения более сложной задачи, она делит эту задачу на две части: одну часть, которую функция умеет решать, и другую, которую функция решать не умеет. Чтобы сделать рекурсию выполнимой, последняя часть должна быть похожа на исходную задачу, но быть по сравнению с ней несколько проще или несколько меньше. Поскольку эта новая задача подобна исходной, функция вызывает новую копию самой себя, чтобы начать работать над меньшей проблемой — это называется рекурсивным вызовом, или шагом рекурсии. Шаг рекурсии включает ключевое слово return, так как в дальнейшем его результат будет объединен с той частью задачи, которую функция умеет решать, и сформируется конечный результат, который будет передан обратно в исходное место вызова, возможно, в main.
Шаг рекурсии выполняется до тех пор, пока исходное обращение к функции не закрыто, т.е. пока еще не закончено выполнение функции. Шаг рекурсии может приводить к большому числу таких рекурсивных вызовов, поскольку функция продолжает деление каждой новой подзадачи на две части. Чтобы завершить процесс рекурсии, каждый раз, как функции вызывает саму себя с несколько упрощенной версией исходной задачи, должна формироваться последовательность все меньших и меньших задач, в конце концов, сходящаяся к базовой задаче. В этот момент функция распознает базовую задачу, возвращает результат предыдущей копии функции, и последовательность возвратов повторяет весь путь назад, пока не дойдет до первоначального вызова и не возвратит конечный результат в функцию main.
Недостаток рекурсии: повторный запуск рекурсивного механизма вызовов функции приводит к росту накладных расходов: к нарастающим затратам процессорного времени и требуемого объема памяти.
Как пример рассмотрим рекурсивную программу для расчета факториала.
Факториал неотрицательного целого числа n, записываемый как n!, равен n*(n-1)*(n-2)*…*1, причем считается, что 1! = 1 и 0! = 1. Например, 5! вычисляется как 5 x 4 x 3 x 2 x 1 и равен 120.
Факториал целого числа, number, большего или равного 0, может быть вычислен итеративно(нерекурсивно) с помощью оператора for следующим образом:
factorial = 1;
for (int counter = number; counter >=1; counter--)
factorial *= counter;
Теперь используем рекурсию для вычисления и печати факториалов целых чисел от 0 до 10. Рекурсивная функция factorial сначала проверяет, истинно ли условие завершения рекурсии, т.е. меньше или равно 1 значение number. Если действительно number меньше или равно 1, factorial возвращает 1, никаких дальнейших рекурсий не нужно и программа завершает свою работу. Если number больше 1, оператор
return number * factorial (number - 1);
представляет задачу как произведение number и рекурсивного вызова factorial, вычисляющего факториал величины number-1. Отметим, что factorial (number - 1) является упрощенной задачей по сравнению с исходным вычислением factorial (number).
В объявлении функции factorial указано, что она получает параметр типа unsigned long и возвращает результат типа unsigned long. Это является краткой записью типа unsigned long int. Описание языка C++ требует, чтобы переменная типа unsigned long int хранилась по крайней мере в 4 байтах (32 битах), и таким образом могла бы содержать значения в диапазоне по крайней мере от 0 до 4294967295. (Тип данных long int также хранится по крайней мере в 4 байтах и может содержать значения по крайней мере в диапазоне от 2147483647). Функция factorial начинает вырабатывать большие значения так быстро, что даже unsigned long не позволяет нам напечатать много значений факториала до того, как будет превышен допустимый предел переменной unsigned long.
// Рекурсивная функция факториала
# include < iostream >
unsigned long factorial (unsigned long);
main ()
{ for (int i = 0; i <= 10; i++)
cout << i << “! = “ << factorial (i) << endl;
return 0;
}
// рекурсивное описание функции вычисления факториала
unsigned long factorial (unsigned long number)
{ if (number <= 1) return 1;
else return (number * factorial (number – 1);
}