1° Предел суммы/разности двух функций равен сумме/разности их пределов:
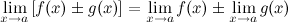
Пример
Задание. Вычислить предел 
Решение. Воспользуемся первым свойство, разложим функцию на несколько более простых и отдельно найдем их пределы.
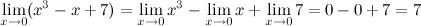
Ответ. 
2° Предел произведения двух функций равен произведению их пределов:
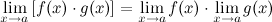
Пример
Задание. Вычислить предел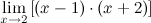 
Решение. Воспользуемся вторым свойство, разложим функцию на несколько более простых и отдельно найдем их пределы.
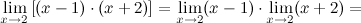
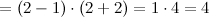
Ответ. 
3° Предел частного двух функций равен частному их пределов, при условии, что предел знаменателя не равен нулю:
Пример
Задание. Вычислить предел 
Решение. Воспользуемся третьим свойство, сделаем числитель и знаменатель функции отдельными пределами и независимо найдем их.
Ответ.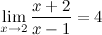 
4° Константу можно выносить за знак предела:
Пример
Задание. Вычислить предел 
Решение. Воспользуемся первым и четвертым свойствами, разложим функцию на несколько более простых и отдельно найдем их пределы.
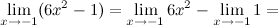
Ответ. 
5° Предел степени с натуральным показателем равен степени предела:
Пример
Задание. Вычислить предел 
Решение. Воспользуемся пятым свойством, внесем предел под третью степень. Сначала найдем предел более простой функции, а затем возведем его в третью степень.
Ответ.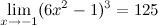 
Первый замечательный предел:
Определение
Предел отношения синуса к его аргументу равен единице в случае, когда аргумент стремится к нулю.
Применение первого замечательного предела на практике
Пример
Задание. Найти предел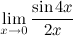 
Решение. Воспользуемся заменой и первым замечательным пределом.
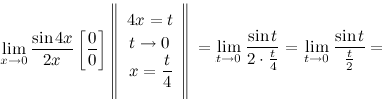
Ответ. 
Пример
Задание. Найти предел 
Решение. Разложим тангенс на синус и косинус и воспользуемся свойствами пределов.
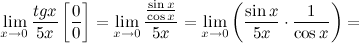
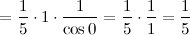
Ответ. 
Второй замечательный предел:
здесь е - число Эйлера.
Пример
Задание. Найти предел 
Решение. Подставим 
, получим неопределенность и для решения предела воспользуемся вторым замечательным пределом.
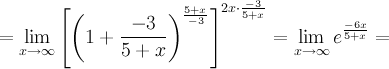
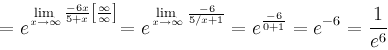
Ответ. 
Следствия из второго замечательного предела
1°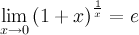 
2°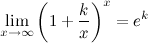 
3° 
4°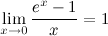 
5° 
6° 
Понятие непрерывности функции в точке
Основные понятия и определения
Функция 
называется непрерывной в точке 
, если:
1. функция определена в точке и ее окрестности;
2. существует конечный предел функции в точке ;
3. это предел равен значению функции в точке , т.е.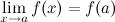 
Пример
Задание. Вычислить предел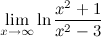 
Решение. 
Ответ. 
Приращение аргумента и функции
Рассмотрим функцию 
, которая определена в некотором интервале 
и рассмотрим произвольную точку 
из этого интервала: 
.
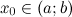Определение
Приращением аргумента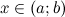 
в точке называется разность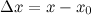 
Замечание. Из последнего равенства легко увидеть, что 
.
Приращением функции 
в точке называется разность соответствующих значений функции 
или, используя равенство из выше приведенного замечания, будем иметь:
Теорема
Функция непрерывна в точке тогда и только тогда, когда бесконечно малому приращению аргумента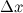 
соответствует бесконечно малое приращение функции 
:
Теорема
Если функции и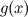 
непрерывны в точке , то функции 
, 
, 
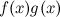также непрерывны в точке .
Пусть функция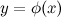 
задана на множестве 
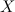, а 
- множество значений этой функции. Пусть на множестве задана функция 
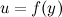. Тогда говорят, что на множестве 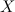задана композиция функций (или сложная функция) 
.
Теорема
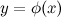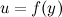Пусть функция непрерывна в точке , а функция непрерывна в точке 
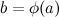. Тогда композиция функций непрерывна в точке .
Теорема
Каждая элементарная функция, заданная в окрестности некоторой точки, непрерывна в этой точке.