ТЕОРИЯ УВД
Методические указания
По выполнению курсовой и контрольной работ
Теория УВД: метод. указания по выполнению курсовой и контрольной работ. – 19 с.
Содержат краткие теоретические сведения и методические указания по выполнению курсовой работы по теме «Оптимизация потока в транспортной сети» и контрольной работы по теме «Решение задачи линейного програм- мирования».
Предназначены для курсантов и студентов заочной формы обучения спе-
циализации 160505.65.01 – Управление воздушным движением.
ОГЛАВЛЕНИЕ
Введение.............................................................................................................................3
Краткие теоретические сведения по теме «Теория графов и сетей
при моделировании процессов УВД»..............................................................................4
Задачи планирования на сетях....................................................................................4
Матрица смежности и матрица инциденций............................................................9
Методические указания по выполнению курсовой работы по теме
«Оптимизация потока в транспортной сети»................................................................11
Требования к содержанию........................................................................................11
Требования к оформлению.......................................................................................13
Рекомендуемая литература.......................................................................................13
Краткие теоретические сведения по теме «Методы оптимизации
процессов в системе УВД. Задача линейного программирования»...........................13
Графическая интерпретация задач линейного программирования......................14
Методические указания по выполнению контрольной работы по теме
«Решение задачи линейного программирования»........................................................17
Общие требования.....................................................................................................17
Рекомендуемая литература................................................................................ 18
ВВЕДЕНИЕ
Система обслуживания воздушного движения (ОВД) относится к слож- ным эргатическим системам управления динамическими объектами. Терми- ны «система», «управление», «динамические объекты» – фундаментальные понятия теории УВД. Каждая реально существующая система состоит из конкретных объектов: технических устройств, людей, управляющих ими и т. д., рассматриваемых как единое целое.
Организация воздушного движения в объеме пространства целой страны сама по себе является сложнейшей проблемой. Эта сложность значительно возрастает с учетом интенсивности воздушного движения и таких особенно- стей УВД, как существенная неравномерность плотности воздушного движе- ния в разных районах и их пропускной способности. Проблема использова- ния воздушного пространства решается с помощью прикладной теории и считается одной из важнейших. Прикладная теория ОВД основывается на достижениях в области моделирования. Изучение системы ОВД и оптимиза- ция процессов на каждом этапе ее функционирования невозможна без моде- лирования. Качество модели зависит от исследователя, его опыта, способно- стей, а если процесс моделирования зависит от экспериментальных данных, то от их точности и полноты.
Контрольная работа выполняется курсантами (студентами) 2-го и 3-го курсов после изучения тем № 8 «Общая характеристика задач оптимизации» и № 10 «Методы оптимизации процессов в системе ОВД».
Выполнение курсовой работы требует знания всего тематического содер- жания дисциплины «Теория УВД» и необходимо для формирования у обу- чающихся умений и навыков нахождения условий оптимизации использова- ния воздушного пространства в соответствии с критериями эффективности и этапами функционирования системы ОВД.
Данная курсовая работа является промежуточным контролем знаний обу- чающихся на 3-м курсе. Курсанты (студенты), не сдавшие и не защитившие курсовую работу в срок, к экзамену не допускаются.
КРАТКИЕ ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ ПО ТЕМЕ
«ТЕОРИЯ ГРАФОВ И СЕТЕЙ ПРИ МОДЕЛИРОВАНИИ ПРОЦЕССОВ УВД»
При исследовании сложных систем используются, в основном, три вида моделей: математические модели, физические модели и графы систем (ико- нографические модели). Граф или орграф представляет собой модель систе- мы объектов, связанных между собой определенными отношениями.
В такой модели объекты можно изобразить в виде множества точек, соеди- ненных между собой линиями. Эти точки в модели называют вершинами (они могут означать любые объекты), а линии, их соединяющие, – связями. В графе линии называют ребрами или дугами.
Ориентированный граф представляет собой граф, в котором обозначены вход (исток) и выход (сток), а стрелками указано направление. В ориенти- рованном графе вершины подлежат маркировке (нумерация может быть произвольная).
В виде графа можно изобразить информационные связи между объекта- ми, например, линии связи между аэродромными службами и диспетчерски- ми пунктами. Граф может служить моделью отношения «часть–целое» и по- казывать, из чего состоит тот или иной агрегат.
Масштабное изображение графа не принципиально, так как здесь не отображаются реальные расстояния между объектами.
Орграф дает возможность наглядного отображения взаимосвязи объектов реальной системы, что позволяет решать множество задач в различных пред- метных областях. Задачи планирования потока в транспортной сети относят- ся к одному из возможных классов задач, решаемых с помощью графов.
Задачи планирования на сетях
К классу потоковых задач (задач планирования потока на сетях) можно отнести следующую задачу:
Имеется система, модель которой может быть представлена в виде ори- ентированного графа. На вход системы поступает поток с некоторой ин- тенсивностью . Пропускная способность элементов системы ограничена.
Необходимо так спланировать поток ВС, чтобы не нарушались ограничения пропускной способности элементов системы и интенсивность потока была максимальной (или равной требуемой величине).
В реальной системе процессы определяются такими характеристиками, как интенсивность воздушного движения и пропускная способность воздуш- ных трасс. Задача формулируется как задача распределения потока воздуш- ного движения из некоторого пункта s в пункт t по сети воздушных трасс, имеющих ограниченную пропускную способность. Могут быть добавлены и другие условия, ограничения и критерии распределения потока.
Например, с учетом вертикального эшелонирования, сокращенных интер- валов и т. д. для подобных задач используются алгоритмы решения потоко- вых задач на транспортных сетях.
Под моделью транспортной сети понимается ориентированный граф, в котором выделяются две вершины, s – исток (источник) и t – сток, а дугам присвоен вес, означающий пропускную способность или расстояние в кило- метрах, и заданы минимальные безопасные интервалы. Пропускную способ- ность дуги u обозначим как (u). Пропускная способность пути, предполо- жим, пути s в t Р (s, t), равна наименьшей из пропускных способностей дуг, в
него входящих:
[ Р (s, t)] = min [(u 1), (u 2), (u 3),...].
Интенсивность потока в сети (далее – поток) обозначим (s, t), поток в дуге – (u). На рис. 1 показан пример простой сети. Цифрами обозначена текущая интенсивность потока в дуге, а в скобках указаны пропускные спо- собности дуг (u). Заметим, что на изображенной сети распределен поток с интенсивностью (u) = 2, причем все объекты потока перемещаются по од- ному пути.
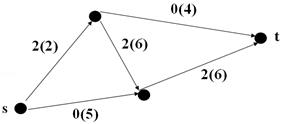
Рис. 1. Пример транспортной сети
Поток представляет собой совокупность ВС, следующих по сети из s в t, причем эти ВС могут быть распределены по дугам сети различным образом. Допустимый поток должен удовлетворять следующим условиям:
1) весь поток, поступающий на вход, достигает выхода сети, т. е.
(s, xi) = (xj, t) = 0,
|
2) интенсивность потока в любой дуге сети удовлетворяет соотношению:

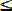 0 (u) (u);
0 (u) (u);
3) для любой вершины все объекты, входящие в нее, также выходят, т. е.
(xj, хk) – (xk, хi) = 0,
где хj Х +(хk), хi Х – (хk).
Введем величину d, которая будет характеризовать возможное прираще- ние потока. Для дуги d (u) = (u) – (u), если поток пропускаем в направлении ориентации дуги, и d = (u), если речь идет о встречном потоке (т. е. условно предполагается, что имеющийся поток величиной (u) можно уменьшить для того, чтобы пропустить во встречном направлении определенное количество единиц потока). Для некоторого пути из s в t Р (s, t) приращение определяется как наименьшее из приращений дуг, в него входящих:
d [ Р (s, t)] = min [ d (u 1), d (u 2), d (u 3),...].
Задача поиска максимального допустимого потока в сети решается с по- мощью алгоритма последовательного увеличения заданного начального по- тока с распределением приращения потока по дугам так, чтобы соблюдались условия допустимого потока, т. е. не нарушались минимально безопасные интервалы. Вариант такого алгоритма, основанного на использовании оргра- фа приращений, приведен в [1].
Рассмотрим, что такое орграф приращений. Этот граф строится из ис- ходной сети при данном значении потока в сети и обозначается как I (Н, i). Напомним, что символом Н обозначается любой орграф, но в данном случае это обозначение исходной сети; i – поток в сети на i -м цикле работы алго- ритма ( i = (s, t)). Используются следующие правила построения орграфа приращений:
1. Каждой дуге сети ставятся в соответствие две дуги орграфа прираще- ний – сонаправленная и противонаправленная. Обозначим их как w 1 и w 2 со- ответственно.
2. Каждой дуге орграфа приращений присваивается вес по следующим правилам:
– (w 1) = 0, если в соответствующей дуге сети Н выполняется (u) < (u);
– (w 1) = ∞, если (u) (u);
– (w 2) = 0, если (u) = 0;
– (w 2) = ∞, если (u) = 0.
То есть вес дуги орграфа приращений равен нулю, если в соответствую- щей дуге сети можно изменить (увеличить или уменьшить) поток. На рис. 2 приведен пример орграфа приращений I (Н, 2) для сети с потоком, равным 2 (см. рис. 1). Цифрами 1 и 2 показаны номера вершин.
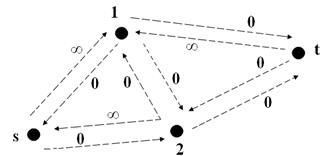
Рис. 2. Орграф приращений I (Н, 2) для сети, изображенной на рис. 1
Запишем алгоритм решения задачи поиска максимального допустимого потока в транспортной сети.
1. i = 1, произвольно выбирается и распределяется по дугам в соответ- ствии с требованиями допустимости начальный поток i (s, t) (он может быть нулевым).
2. Строится орграф приращений I (Н, i).
3. На I (Н, i) выбирается путь Р (s, t), длина которого равна 0. Если такого пути нет, – конец работы алгоритма и i – максимальный допустимый поток.
4. На исходной сети определяется последовательность дуг, соответствую-
щая выбранному пути на I (Н, i), и по их приращениям находится d [ Р (s, t)]
по формуле, приведенной выше.
5. Определяется новый поток i +1= i + d [ Р (s, t)] для каждой дуги, соответ- ствующей пути Р (s, t). Дополнительные единицы потока распределяются по этим дугам (необходимо нарисовать сеть заново с вновь полученным пото- ком на ней).
6. i = i + 1, далее следует перейти на шаг 2.
Пример. Первый цикл работы алгоритма, i = 1. Возьмем сеть, изображен-
ную на рис. 1. Начальный поток равен 2.
Шаг 1. Строим орграф приращений I (Н, 2) (см. рис. 2).
Шаг 2. На орграфе приращений выбираем путь нулевой длины Р (s, 2, t).
Шаг 3. Находим приращение d [ Р (s, 2, t)] = min [5, 4] = 4.
Шаг 4. Новый поток 2 = 1 + 4 = 2 + 4 = 6. Получаем сеть с распределен-
ным новым потоком (рис. 3.)
Рис. 3. Сеть с полученным потоком (s, t) = 6
после первого цикла работы алгоритма
Второй цикл работы алгоритма, i = 2.
Шаг 2. Строим орграф приращений I (Н, 6) (рис. 4).
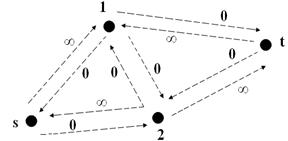
Рис. 4. Орграф приращений I (Н, 6) для сети
Шаг 3. На I (Н, 6) находим единственный путь нулевой длины Р (s, 2, 1, t).
Шаг 4. Находим приращение d [ Р (s, 2, 1, t)] = min [1, 2, 4] = 1.
Шаг 5. Новый поток 1 = 2 + 1 = 6 + 1 = 7. Получаем сеть с распределен-
ным новым потоком (рис. 5).
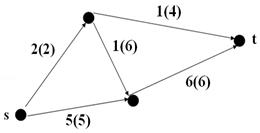
Рис. 5. Сеть с полученным потоком (s, t) = 7
после второго цикла работы алгоритма
Полученный поток является искомым максимальным допустимым пото- ком, т. к. если построить новый орграф приращений, то в нем не найдется пу- ти нулевой длины из s в t.
Существуют более сложные, и в то же время практически более значимые варианты потоковых задач, такие как планирование максимального потока наименьшей стоимости, планирование потока в сети, где пропускная способ- ность дуг меняется со временем и др. Алгоритмы решения этих и других за- дач представлены в [2].