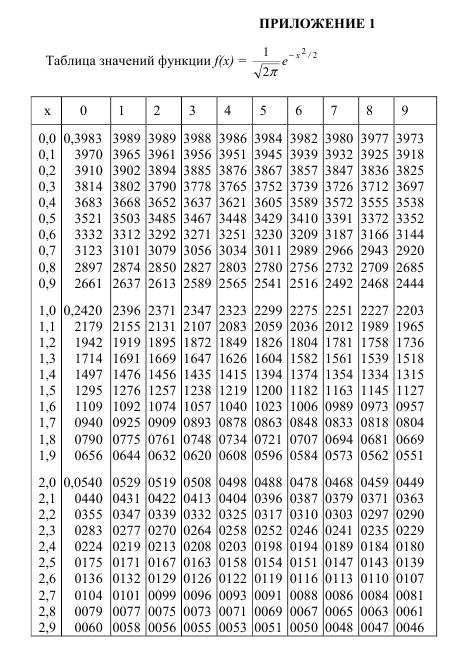
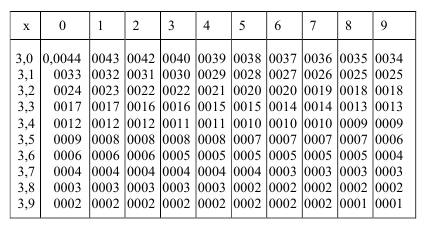
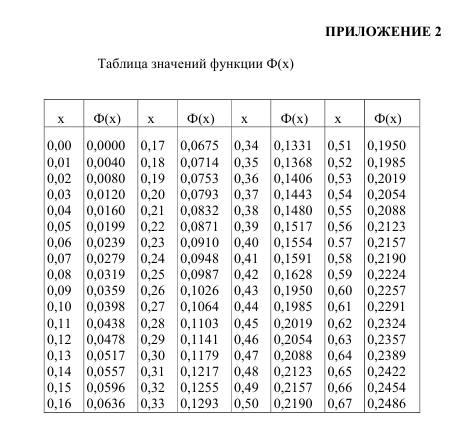
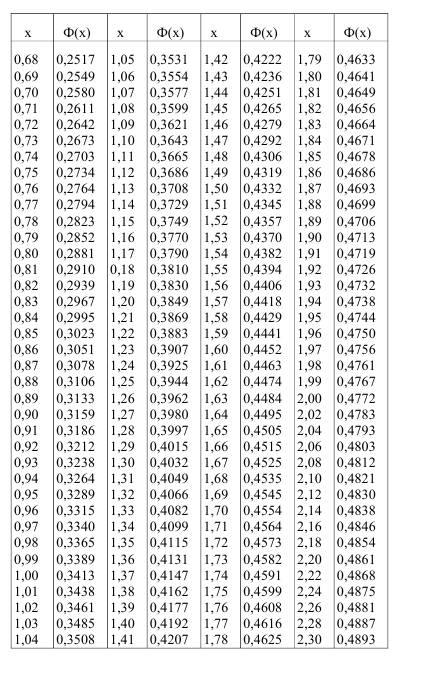
Вариант 1
Монету бросают пять раз. Найти вероятность того, что «герб» выпадет: а) менее двух раз.
Вариант 2
Монету бросают семь раз. Найти вероятность того, что «герб» выпадет не менее трех раз.
Вариант 3
Найти вероятность того, что событие А появится не менее трех раз в четырех независимых испытаниях, если вероятность появления события А в одном испытании равна 0,4;
Вариант 4
Устройство состоит из трех независимо работающих основных элементов. Устройство отказывает, если откажет хотя бы один элемент. Вероятность отказа каждого элемента за время t равна 0,1. Найти вероятность безотказной работы устройства за время t
Вариант 5
В семье пять детей. Найти вероятность того, что среди этих детей два мальчика. Вероятность рождения мальчика принять равной 0,51.
Вариант 6
В семье пять детей. Найти вероятность того, что среди этих детей не более двух мальчиков. Вероятность рождения мальчика принять равной 0,51.
Вариант 7
В семье пять детей. Найти вероятность того, что среди этих детей: более двух мальчиков. Вероятность рождения мальчика принять равной 0,51.
Вариант 8
В семье пять детей. Найти вероятность того, что среди этих детей не менее двух и не более трех мальчиков. Вероятность рождения мальчика принять равной 0,51.
Вариант 9
Найти вероятность того, что событие А наступит ровно 70 раз в 243 испытаниях, если вероятность появления этого события в каждом испытании равна 0,25.
Вариант 10
Вероятность появления события в каждом из 2100 независимых испытаний равна 0,7. Найти вероятность того, что событие появится не менее 1470 и не более 1500 раз;
Задание №5. Закон распределения случайной величины
Вариант 1
Устройство состоит из трех независимо работающих элементов. Вероятность отказа каждого элемента в одном опыте равна 0,1. Составить закон распределения числа отказавших элементов в одном опыте. Найти математическое ожидание и дисперсию случайной величины Х.
Вариант 2
В партии 10% нестандартных деталей. Наудачу отобраны четыре детали. Написать биномиальный закон распределения дискретной случайной величины X—числа нестандартных деталей среди четырех отобранных. Найти математическое ожидание и дисперсию случайной величины Х.
Вариант 3
Написать биномиальный закон распределения дискретной случайной величины X—числа появлений «герба» при трех бросаниях монеты. Найти математическое ожидание и дисперсию случайной величины Х.
Вариант 4
Две игральные кости одновременно бросают два раза. Написать биномиальный закон распределения дискретной случайной величины X—числа выпадений четного числа очков на двух игральных костях. Найти математическое ожидание и дисперсию случайной величины Х.
Вариант 5
Устройство состоит из трех независимо работающих элементов. Вероятность отказа каждого элемента в одном опыте равна 0,3. Составить закон распределения числа отказавших элементов в одном опыте. Найти математическое ожидание и дисперсию случайной величины Х.
Вариант 6
В партии 20% нестандартных деталей. Наудачу отобраны четыре детали. Написать биномиальный закон распределения дискретной случайной величины X—числа нестандартных деталей среди четырех отобранных. Найти математическое ожидание и дисперсию случайной величины Х.
Вариант 7
Написать биномиальный закон распределения дискретной случайной величины X—числа появлений «герба» при четырех бросаниях монеты. Найти математическое ожидание и дисперсию случайной величины Х.
Вариант 8
Две игральные кости одновременно бросают два раза. Написать биномиальный закон распределения дискретной случайной величины X—числа выпадений нечетного числа очков на двух игральных костях. Найти математическое ожидание и дисперсию случайной величины Х.
Вариант 9
Устройство состоит из четырех независимо работающих элементов. Вероятность отказа каждого элемента в одном опыте равна 0,1. Составить закон распределения числа отказавших элементов в одном опыте. Найти математическое ожидание и дисперсию случайной величины Х.
Вариант 10
В партии 10% нестандартных деталей. Наудачу отобраны шесть деталей. Написать биномиальный закон распределения дискретной случайной величины X—числа нестандартных деталей среди шести отобранных. Найти математическое ожидание и дисперсию случайной величины Х.