Моделирование химико-технологических процессов

240100.62 Химическая технология,

профиль подготовки Химическая технология природных энергоносителей и углеродных материалов

1. Химическое производство как химико-технологическая система (ХТС).

Производственные процессы в химической промышленности и сходных ей областях характеризуются большим разнообразием выпускаемой продукции и большой сложностью. Условия протекания отдельных стадий могут быть весьма различными: от высоких температур (~1500 ⁰С) в случае электрокрекинга углеводородов до очень низких температур при разделении воздуха, от высоких давлений при производстве аммиака и метанола до низких в процессах вакуумной перегонки. Одни процессы проводят в водной фазе, в других даже следовые количества воды могут полностью дезорганизовать процесс. Технологические схемы получения того или иного продукта могут быть более или менее компактными.

Несмотря на существенные качественные и количественные различия отдельных технологических процессов, разнообразие комбинаций аппаратов, используемых для их реализации, различные мощности и условия протекания, все они имеют общие свойства.

Каждое производство в соответствии с общей теорией систем является сложной системой, которая называется химико-технологической системой.

Химико-технологические системы (ХТС) представляют собой совокупность физико-химических процессов и средств их осуществления с целью получения продукта заданного количества и в требуемом количестве.

2. Иерархическая структура химического производства.

 

 

Рис. 1.4. Иерархическая структура химико-технологической системы

 

Элементом минимального масштаба в структуре ХТС является отдельный аппарат (реактор, абсорбер, ректификационная колонна, насос и прочее). Это – низший масштабный уровень I. Объединение нескольких аппаратов, выполняющих вместе какое-либо преобразование материального потока, образует один элемент подсистемы II-го масштабного уровня (реакционный узел, система разделения многокомпонентной смеси и так далее). Совокупность подсистем второго уровня образует подсистему III-го уровня в виде элементов, которые называются отделениями, участками, цехами. Например, в производстве серной кислоты это отделения обжига серосодержащего сырья, очистки и осушки сернистого газа и т.д. К подсистемам III-го уровня могут относиться водоподготовка, регенерация отработанных вспомогательных материалов, утилизация отходов

3. Основные элементы и подсистемы ХТС.

 

 

4. Постановка задачи создания химико-технологических процессов в терминах теории систем.

 

5. Задача анализа ХТС.

 

 

6. Задача синтеза ХТС.

 

7. Задача оптимизации ХТС.

 

 

8. Свойства ХТС.

 

9. Виды моделей ХТП.

 

 

10. Обобщённые (качественные) модели ХТП. Химическая модель.

 

11. Обобщённые (качественные) модели ХТП. Операционно-описательная модель.

 

 

12. Обобщённые (качественные) модели ХТП. Функциональная и структурная схемы.

 

13. Операторная схема ХТС. Технологические операторы.

 

 

14. Типы технологических связей в ХТП.

 

15. Замкнутая и разомкнутая ХТС.

 

 

16. Технологическая схема ХТП.

 

17. Математическая модель элемента ХТС.

Математические модели ХТС содержат информацию о величине потоков идущих через элементы систем то есть содержат количественную информацию. Математические модели могут быть символическими и иконно-графическими. Символические модели(аналитические) представляют собой набор математических функций описывающих поведение отдельных элементов процесса.

 

18. Иконографические математические модели ХТП. Аналитическая модель.

Иконографические математические модели связаны с изображением определенной последовательности выполнения операции при анализе ХТС.

19. Иконографические математические модели ХТП. Топологические модели (графы).

Графы – указывают последовательность операций в которых происходит изменение исследуемого свойства процесса (граф - топологическая модель системы, может быть составлен для любого свойства системы на пример потоковый граф общего материального баланса по индивидуальному веществу, тепловой потоковый граф и так далее) Графы состовляют на основе операторной технологической схемы. Граф представляет собой конфигурацию отдельных точек или кружочков каждый из которых отвечает аппарату или технологической операции в которой происходит изменение свойства. Точки или кружки называются вершинами или узлами. Узлы соединяются отрезками прямых, ломанных, или кривых линий со стрелками, указывающих направление потока. Над дугами приводят числа количественно изменяющие направление потоков. Потоковый граф дополняют узлами из которых поступает сырьё или энергия

 

20. Иконографические математические модели ХТП. Структурная блок-схема.

Все модели ХТС можно разделить на два вида: качественные (обобщенные) и математические, которые в свою очередь делятся на ряд разновидностей.

Качественные (обобщенные) модели существуют двух видов: операционно-описательные и иконографические.

Операционно-описательные модели — это словесное описание процесса функционирования системы. В нем приводятся основные химические реакции, по которым осуществляется получение целевого продукта (химическая схема процесса), дается описание процессов, происходящих в аппаратах системы, приводятся сведения о составе сырья, значениях параметров технологического режима и т. п. На практике операционно-описательная модель — это различные виды проектно-конструкторской документации, технологические регламенты.

Иконографические модели всегда связаны с наглядным графическим изображением, чертежом. Обобщенные иконографические модели дают лишь качественное представление о функционировании системы. Это различные виды схем химико-технологического процесса, выполненные в виде чертежей. Существует несколько разновидностей таких схем: функциональная (принципиальная), структурная, операционная (операторная), технологическая.

21. Материальные балансы ХТС.

 

 

22. Энергетические балансы ХТС.

 

23. Технологические принципы создания ХТП. Принцип глубины и полноты переработки сырья.

 

 

24. Технологические принципы создания ХТП. Принцип минимизации энергетических затрат.

 

25. Технологические принципы создания ХТП. Принцип минимизации отходов и защиты окружающей среды от промышленных выбросов.

 

 

26. Технологические принципы создания ХТП. Концепция оптимального использования оборудования.

 

27. Способы синтеза структуры ХТС: метод перебора вариантов структуры и топологии (интегрально-гипотетический метод).

1) Перебор вариантов и структуры топологии: Перебор вариантов топологии состава и параметров функционирования системы не имея дополнительной информации то может быть синтезировано большое количество вариантов, сократить количество вариантов можно используя хорошо известные зависимости на пример: известно что тепло от холодных тел горячим не переходит, известно, что вещество распространяется из зоны высокой концентрации в зону низкой и так далее пользуясь этими правилами можно исключить из рассмотрения значительную часть вариантов синтеза ХТС.

2) декомпозиционный метод синтеза

3) эвристический метод

4) эволюционный метод

28. Способы синтеза структуры ХТС: декомпозиционный метод синтеза.

1) Перебор вариантов и структуры топологии

2) декомпозиционный метод синтеза: Метод декомпозиции в соответствии с этим методом общую задачу синтеза разбивают на несколько уровней, на пример: при двухуровневой декомпозиции на верхнем уровне рассматривается синтез взаимодействия отдельных подсистем.

 

 

	Подсистема химических процессов		Подсистема теплообмена		Подсистема разделения продуктов		Подсистема управления

 

 

На нижнем уровне синтезируют структуру каждой подсистемы в отдельности из отдельных элементов, структура каждой подсистемы может быть разнообразной и иметь ряд вариантов, если при анализе выяснится, что какой-то из вариантов неосуществим, то его отбрасывают и общее количество вариантов требующих расчета сокращается, чем достигается экономия средств и времени.

 

3) эвристический метод

4) эволюционный метод

 

29. Способы синтеза структуры ХТС: эвристический метод.

1) Перебор вариантов и структуры топологии

2) декомпозиционный метод синтеза

3) Эвристический принцип синтеза многоуровневая декомпозиция синтеза ХТС заключается в способности высококвалифицированных специалистов интуитивно выбирать наиболее удачные варианты решения проблемы без полного перебора всех существующих вариантов, принятие решения происходит без его познавания с помощью доказательств, только на основе обобщенного опыта и знаний специалиста.

 

4) эволюционный метод

30. Способы синтеза структуры ХТС: эволюционный метод.

1) Перебор вариантов и структуры топологии

2) декомпозиционный метод синтеза

3) эвристический метод

4) Эволюционный принцип основе с использованием метода эвристики и перебором вариантов, на основе анализа выбирается узкое место ХТС выбирается критерий оптимальности и проводится расчет, далее проводится модификация подсистемы являющаяся узким местом и вновь повторяется расчет, на основе расчета проводится поиск нового узкого места, модернизация схемы и так далее. То есть эволюционный принцип подразумевает последовательное повторение этапов синтеза, анализа, модификации структуры до получения оптимального результата (метод последовательных приближений) (итераций)

 

 

 

31. Анализ качества функционирования (расчёт) ХТС. Интегральный метод расчёта.

Анализ заключается в анализе структуры ХТС и в анализе качества функционирования ХТС цель анализа структуры ХТС заключается в выявлении её структурных особенностей и определении оптимальной последовательности расчета элементов структуры

Анализ качества функционирования ХТС заключается в расчете и в получении количественных оценок основных свойств системы на пример: чувствительности, надежности, устойчивости.

Задача расчета ХТС заключается в получении количественных характеристик как режимов функционирования отдельных элементов системы,так и всей системы в целом. При расчете при заданных параметрах функционирований операторов находят параметры состояния потоков связывающих эти операторы. Задача расчета ХТС является сложной для решения этой задачи используют две группы методов: 1 интегральный или композиционный метод 2 декомпозиционный. суть интегральных методов расчета ХТС заключается в объединении уравнений описывающих работу отдельных аппаратов в одну большую систему уравнений с решением этой системы

)

 

 

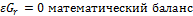
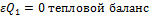
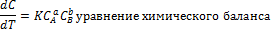
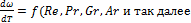Описание элементов схемы

 

Объединяются все системы уравнений и проводится расчет используют как линейные уравнения, так и дифференциальные нелинейные уравнения химической кинетики и гидравлики, такая система уравнений называется смешанной. Кроме того интегральный метод требует математической подготовки и знание специального программного обеспечения для решения уравнение, применение композиционного метода оправдано только для простых производств, или если необходимо просчитать только линейные системы уравнений: найти материальный или тепловой баланс процесса.

32. Анализ качества функционирования (расчёт) ХТС. Декомпозиционный метод расчёта.

Анализ заключается в анализе структуры ХТС и в анализе качества функционирования ХТС цель анализа структуры ХТС заключается в выявлении её структурных особенностей и определении оптимальной последовательности расчета элементов структуры

Анализ качества функционирования ХТС заключается в расчете и в получении количественных оценок основных свойств системы на пример: чувствительности, надежности, устойчивости.

Задача расчета ХТС заключается в получении количественных характеристик как режимов функционирования отдельных элементов системы,так и всей системы в целом. При расчете при заданных параметрах функционирований операторов находят параметры состояния потоков связывающих эти операторы. Задача расчета ХТС является сложной для решения этой задачи используют две группы методов: 1 интегральный или композиционный метод 2 декомпозиционный. суть интегральных методов расчета ХТС заключается в объединении уравнений описывающих работу отдельных аппаратов в одну большую систему уравнений с решением этой системы

)

 

 

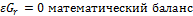
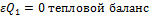
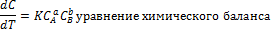
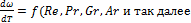Описание элементов схемы

Суть декомпозиционного метода заключается в том, что процесс в целом представляется в виде отдельных блоков каждый из которых соответствует отдельному элементу ХТС, расчет сводится к последовательному расчету отдельных блоков в этом случае система уравнений содержит небольшое количество уравнений описывающих отдельный блок, такое математическое описание отдельных блоков давно разработано, описано в литературе и существует в виде компьютерных программ по этому декомпозиционный метод расчета получил распространение при проектировании технологических процессов

 

33. Анализ качества функционирования (расчёт) ХТС. Итерационный метод расчёта замкнутых ХТС.

Большинство ХТС имеют рециркуляционное соединение образующие замкнутую систему непосредственность такой системы декомпазиционным принципом невозможно поэтому систему приводят к разомкнутому виду, проводят расчет каждого элемента методом последовательных приближений или итерационным методом.

34. Анализ структуры (последовательности расчёта) ХТС.

Анализ структур ХТС – при расчете ХТС в основном используют декомпозиционный метод, но при расчете замкнутых ХТС особенно имеющих несколько замкнутых контуров нужно выбрать такой разрыв связей в контуре, что бы минимизировать количество расчетов, это задача анализа структуры ХТС. В процессе анализа структуры ХТС произвольной сложности решаются следующие задачи: а) определить наличие в ХТС групп аппаратов (агрегатов) рассчитываемых совместно и выделить его в виде «комплекса»; б) определить последовательность расчета комплексов и аппаратов не входящих в комплексы; в) для каждого комплекса содержащего замкнутую систему определить оптимальное количество разрываемых потоков для перевода комплекса из замкнутой структуры в разомкнутую; г) определить окончательную последовательность расчета во всей ХТС.

35. Анализ структуры ХТС. Представление ХТП в виде графов.

Граф соответствует технологической схеме, каждая вершина графа отвечает определенному аппарату, а связи между вершинами (дуги) соответствуют материальным потокам. Вершины и дуги графов нумеруют последовательность сцепленных дуг позволяющих пройти от одной вершины к другой называется путем. Путь может быть записан через последовательность дуг или последовательность вершин. Путь начальная вершина которого совпадает с конечной при чем каждая вершина кроме начальной проходит только один раз и называется контуром. Комплексом называется часть графа вершины которого обладают следующими свойствами: каждая из вершин и дуг комплекса входит в один их контуров. Если вершина входит в комплекс, то в комплекс входят все вершины входящие в контуры содержащие эту вершину.

36. Анализ структуры ХТС. Представление ХТП в виде матрицы смежности, списка смежности, таблицы связей.

Матрица смежности:

Для простой схемы не требуется применение специальных программных продуктов, для более сложных схем анализ затруднен по этому анализ структуры ведут при помощи специализированных программ в результате возникает задача ввода в компьютер системной схемы в численном виде, задача может быть решена с использованием матриц смежности, списков смежностей или таблиц связей. Матрица смежности представляет собой двоичную таблицу в которой количество строк и столбцов равны количеству вершин графа. В случае если между вершинами есть связь, то на пересечение соответствующих строк и граф ставят единицу, если связей нет, ставят ноль

Список смежности:

Список смежности представляется в виде таблицы первая строка которой обозначает номер связи (дуги) вторая строка номер вершины выхода третья строка номер вершины входа

Таблицы Связей:

Используют таблицы связей состоящие из 2-х частей часть А является таблицей входных связей в первом столбце которой указывают вершины из которой выходит дуга, а во 2-м столбце вершину в которую входит дуга по второй части таблицы указывают в 1-м столбце указывают вершины в которые входят дуги, а во 2-м от куда выходят.

 

37. Правила определения оптимальной последовательности расчёта ХТС.

Задача определения оптимальной последовательности расчета выполняется в 2-а этапа и решается в 2-а этапа. На первом этапе выполняют анализ структуры ХТС в целом, выделяют комплексы и все контуры входящие в эти комплексы. На 2-м этапе проводят анализ структуры комплекса и определяют связи разрыв которых позволяет перевести комплекс к разомкнутому виду для применения итерационного способа расчета и определяют окончательную последовательность расчета всей системы.

38. Детерминированные или физико-химические модели ХТС: модуль смесителя потоков.

Детерминированные модели, представляют собой математические описания всех процессов протекающих в данном аппарате детерминированная модель включает: материальный баланс, тепловой баланс кинетические уравнения описывающие скорость реакции, термодинамические уравнения уравнения описывающие гидромеханику процесса, уравнения описывающие зависимости различных физико-химических свойств реагирующий веществ от температуры, давления и так далее. Уравнения фазового равновесия, уравнения массопереноса через границу раздела фаз. Это не полный перечень математических уравнения составляющих математическую модель отдельного модуля. Часто в модели вводят упрощения так как расчет даже одного модели элемента оказывается сложным на пример:при расчете реакторов вводят модели идеального смешения, модели идеального вытеснения, позволяющие упростить расчет. Иногда реакторы смешения и вытеснения заменяют ячеичные или диффузионные модели, но тогда в качестве внешних параметров приходится вводить число ячеек или коэффициенты диффузии (подробно смотри химические реакторы) полученную математическую модель модуля проверяют на адекватность сравнивая результаты расчетов с результатами полученными на практике при работе реального аппарата в случает необходимости вводят корректирующие коэффициенты. Формируют программу расчетного модуля для компьютера. Детерминированные модели основаны на теоретически обоснованных законах описывающие данный модуль.

 

G1,T1,X1Q1

 

G3,T3,X3,Q3

 

G2,T2,X2,Q2

 

 

G1,G2,G3 – массовый (мольный) расход количества вещества

Т1,Т2,Т3 – температура потока

Х1,Х2,Х3 – составы потоков (мольные или массовые доли)

Q1,Q2,Q3 – теплоты потоков

Смеситель:

- предназначен для расчета материального и теплового балансов двух вмешивающихся потоков приспользуют следующее упрощение выводе модели смесителя:

1) структура потоков в аппарате, если условие не выполняется, то необходимо либо вводить коэффициент перемешивания, либо рассчитывать гидродинамическую структуру потоков в аппарате, что неоправданно усложняет модель.

2) процесс смешения адиобатический, теплота смешения компонентов не учитывается. На практике потери не превышают 5-ти процентов, а теплота смешения их компенсирует исключение составляют отдельные процессы на пример: смешение серной кислоты с водой.

3) все потоки имеют однофазное состояние то есть либо жидкие, газообразное либо твердые, это допущение позволяет отказаться от расчета фазовых переходов, на практике: для смешения горячего и холодного потоков разного состава могут возникнуть фазовый переход (испарение, конденсация или образование твердой фазы) для таких процессов необходимо использовать модель сепараторов.

4) давление в аппарате постоянное (пренебрегается гидравлическими потерями) постоянство давления исключает фазовый переход

 

 

39. Детерминированные или физико-химические модели ХТС: модуль делителя потоков.

Детерминированные модели, представляют собой математические описания всех процессов протекающих в данном аппарате детерминированная модель включает: материальный баланс, тепловой баланс кинетические уравнения описывающие скорость реакции, термодинамические уравнения уравнения описывающие гидромеханику процесса, уравнения описывающие зависимости различных физико-химических свойств реагирующий веществ от температуры, давления и так далее. Уравнения фазового равновесия, уравнения массопереноса через границу раздела фаз. Это не полный перечень математических уравнения составляющих математическую модель отдельного модуля. Часто в модели вводят упрощения так как расчет даже одного модели элемента оказывается сложным на пример:при расчете реакторов вводят модели идеального смешения, модели идеального вытеснения, позволяющие упростить расчет. Иногда реакторы смешения и вытеснения заменяют ячеичные или диффузионные модели, но тогда в качестве внешних параметров приходится вводить число ячеек или коэффициенты диффузии (подробно смотри химические реакторы) полученную математическую модель модуля проверяют на адекватность сравнивая результаты расчетов с результатами полученными на практике при работе реального аппарата в случает необходимости вводят корректирующие коэффициенты. Формируют программу расчетного модуля для компьютера. Детерминированные модели основаны на теоретически обоснованных законах описывающие данный модуль.

Модель делителя потоков

- в аппарат поступает поток G1 с температурой T1,составом Х1, Q1, в аппарате поток разделяетс на 2-а с расходам G2,G3, температурами Т2,Т3, составами Х2,Х3, и теплосодержанием Q2,Q3, при расчете используют следующие допущения:

1) составы, температуры и давления потоков в аппарате не меняются, изменяются расходы

2) все потоки имеют однофазное состояние, в противном случае необходимо рассчитывать фазовое равновесие, составы и температуры выходящих, потоков получаемые при протекании изоэнтальпийного процесса испарением такой процесс происходит в сепараторах.

Известно 2-а способа деления потока:

Требует знания расхода одного из потоков покидающих аппарат и входного потока тогда G1,G2 известно, но поскольку расчет ведет тупая машина, то в практике расчетов возникает ситуация, когда G2 больше чем G1 и G3становится отрицательным, по этому часто при создании модуля делителя используют 2-й способ задачи деления в виде коэффициента деления потоков, , тогда материальный баланс , тепловой баланс потоков ; ; смотри выше

 

40. Детерминированные или физико-химические модели ХТС: модуль теплообменника.

Детерминированные модели, представляют собой математические описания всех процессов протекающих в данном аппарате детерминированная модель включает: материальный баланс, тепловой баланс кинетические уравнения описывающие скорость реакции, термодинамические уравнения уравнения описывающие гидромеханику процесса, уравнения описывающие зависимости различных физико-химических свойств реагирующий веществ от температуры, давления и так далее. Уравнения фазового равновесия, уравнения массопереноса через границу раздела фаз. Это не полный перечень математических уравнения составляющих математическую модель отдельного модуля. Часто в модели вводят упрощения так как расчет даже одного модели элемента оказывается сложным на пример:при расчете реакторов вводят модели идеального смешения, модели идеального вытеснения, позволяющие упростить расчет. Иногда реакторы смешения и вытеснения заменяют ячеичные или диффузионные модели, но тогда в качестве внешних параметров приходится вводить число ячеек или коэффициенты диффузии (подробно смотри химические реакторы) полученную математическую модель модуля проверяют на адекватность сравнивая результаты расчетов с результатами полученными на практике при работе реального аппарата в случает необходимости вводят корректирующие коэффициенты. Формируют программу расчетного модуля для компьютера. Детерминированные модели основаны на теоретически обоснованных законах описывающие данный модуль.

Модель теплообменника

- является более сложной моделью чем смеситель или делитель потоков, так как при изменении температуры возможно изменение фазового состояния, в связи с этим существуют несколько расчетных моделей теплообменных аппаратов:

1) аппарат газ-газ или жидкость-жидкость без изменения фазового состояния

2) аппарат с фазовым переходом для систем г-г и г-ж это конденсаторы паров, испарители

3) аппарат с фазовым переходом и процессом охлаждения (нагрева)

К 1-му варианту относятся холодильники-конденсаторы ректификационных колонн в которых перегретый пар охлаждается до температуры начала конденсации затем конденсируется, затем охлаждается до заданной температуры.

Ко 2-му варианту относятся обогреватели-испарители применяемые для создания парового орошения колонны кроме того на процесс расчета влияние оказывает конструкция теплообменника и характер движения теплообменивающих средств. Возможно прямоток, противоток, перекрестный ток, поточность теплообменника по трубному пространству, поточность межтрубного пространства и так далее…

 

41. Статистические модели элементов ХТС. Принцип черного ящика.

Статистические модели не включают детальное описание закономерности процесса такие модели создаются по принципу – «черный ящик» и представляют собой набор уравнений линейной и нелинейной регрессии связывающие выходные параметры модуля с входными. Уравнения получают опроксимацией результатов лабораторных исследований объекта (получение математических зависимостей с использований методов меньших квадратов). Регрессионные уравнения могут быть получены с использованием методов математического планирования экспериментов. В любом случае статистическая модель должна адекватно, то есть точно описывать объект (модуль)

 

42. Статистические модели элементов ХТС. Статистическая обработка результатов экспериментов.

Статистические модели

43. Статистические модели элементов ХТС. Регрессионный анализ.

44. Статистические модели ХТС. Методы математического планирования эксперимента. Полный факторный эксперимент.

Цель математического планирования заключается в таком планировании опытов, что бы после обработки результатов по известной методике получить уравнение: y=f(x;х₂;х₃) математическая модель объекта исследования x;х₂;х₃ –факторы измеренные в процессе y – функции отклика, результат модели описывает какую-либо поверхность на первом этапе планирования, пользуется общими представлениями об объекте исследования выбирает факторы не зависимые,то есть не должны влиять друг на друга, а изменяемые откликами должны давать максимальную информацию об объекте, наиболее часто используют полный фагеторный эксперимент, в нем одновременно все факторы изменяют дискретно на определенном числе уровней N=Rⁿ, гдк R-число уровней изменения факторов, n-число факторов, если мы исследуем зависимость от 3-х переменных (n=3)

45. Статистические модели ХТС. Обработка производственных данных методом пассивного эксперимента.

Пассивный эксперимент заключается в математической обработке данных полученных при изучении установки на различных стационарных режимах, без планирования этих режимах

46. Статистические модели элементов ХТС. Корреляционный анализ.

ХТС исп. Методы наименьших квадратов рассчитывает коэффициент парной корреляции R² или r² который позволяет оценить глубину связей между аргументом х и функцией y, r=±1, то существует детерминированное связь между x и y если r=0,то связи нет, на практике хорошей корреляцией считается r=0,98 до 0.99.

47. Статистические модели ХТС. Методы математического планирования эксперимента. Полный и дробный факторный эксперименты.

 

48. Статистические модели ХТС. Методы математического планирования эксперимента. Композиционный план второго порядка.

Для детального изучения области оптимума и участков поверхности отклика со значительной кривизной линейная модель становится неадекватной. В таких случаях для математического описания может быть достаточно полинома второго порядка, реже третьего порядка, полученного используя планы соответственно второго и третьего порядков.

Планы 2-го порядка позволяют получить математическое описание в виде полной квадратичной модели, содержащей кроме основных эффектов b_i все парные взаимодействия b_ij и квадратичные эффекты b_ii.

Подобные планы применяют, как правило, либо в том случае, когда использование планирования первого порядка не позволило получить адекватную регрессионную модель, и выяснилась необходимость ее усложнения, либо если заранее известно, что объект исследования обладает существенными нелинейными свойствами.

Планы 2^k не могут обеспечить получение раздельных оценок коэффициентов b_jj при квадратичных функциях и коэффициента b₀.

Применение полного факторного эксперимента типа 3^k для получения раздельных оценок коэффициентов полинома второго порядка не является рациональным, так как планирование на трех уровнях характеризуется резким увеличением объема эксперимента.

Целесообразнее для этой цели использовать композиционный план, образованный путем добавления некоторого количества специальных точек к «ядру», состоящему из планов 2^k или 2^k–p. Если к «ядру» добавить точку в центре плана с координатами (0, 0...0) и 2k так называемых «звездных» точек с координатами (±α, 0...0), (0, ±α,..0), …, (0, 0... ±α), то получим центральный композиционный план, предложенный Боксом. В качестве ядра используются точки ПФЭ – вершины квадрата и куба соответственно.

Используют эти планы обычно на заключительном этапе исследования: при описании экспериментальной области в ситуациях, когда отсутствует априорная информация об объекте и его полиномиальную модель приходится подбирать последовательно, начиная с простейшего линейного уравнения, которое затем достраивается до полной квадратичной модели. В таких случаях применение композиционных планов оказывается наиболее выгодным по числу опытов.

В зависимости от применяемого критерия оптимальности различают ортогональное и рототабельное композиционное планирование. Рассмотрим ортогональное композиционное планирование, в котором в силу ортогональности матрицы плана все коэффициенты квадратичной модели оцениваются независимо друг от друга.

 

49. Статистические модели ХТС. Оценка значимости коэффициентов регрессии. Оценка адекватности модели.

 

50. Постановка задачи оптимизации ХТС.

При постановке задачи оптимизации необходимо выполнять следующие условия:

1. Определение цели оптимизации, при этом при формулировке цели задачи оптимизации должна задаваться однозначно, по одному критерию оптимизации на пример: задачи оптимизации не может быть «обеспечение максимальной производительности объекта при минимальной скорости» так как при такой формулировке требуется одновременно оптимизировать 2-а показателя: производительность, стоимость. При чем показатели имеют противоположную направленность. Задача оптимизации должна быть сформулирована так: а) обеспечить минимальную стоимость объекта при минимальной стоимость (как правило производительность объекта определяется производственная необходимость данной продукции по этому производительность является исходным параметром при проектировании); б) определить максимальную производительность при заданной стоимости объекта.

2. Оптимизация объекта требует наличие изменяемых параметров влияющих на конечный результат оптимизации (ресурсов оптимизации)

3. Должна существовать возможность количественной оценки оптимизируемой величины иначе невозможно определить эффект при варьировании ресурсов оптимизации

4. Обычно оптимизируемая величина связана с экономичностью работы объекта и выражается какой-то определенной мерой и называется критерием оптимальности.

Задача оптимизации по-разному решается для установившихся процессов и для динамических (изменяющихся) процессов. Для установившихся процессов решается задача статической оптимизации заключающаяся в создании и реализации оптимальной модели процесса. Для неустановившихся процессов решается задача динамической оптимизации, заключающаяся в реализации системы оптимального управления процессом.