Содержание и рекомендации
Приводимые выше показательные неравенства взяты из книги “ЕГЭ по математике. Практическая подготовка к заданию С3” /М.:ИЛЕКСА, 2014; автор: Волков Д. А./.
Показательные неравенства разбиваются на типы: неравенства, решаемые одним методом, находятся в одном номере, а разными методами – в разных номерах.
Методы решения для показательных неравенств каждого типа приведены в выше упомянутой книге. Но они также приводятся ниже.
Данные неравенства можно использовать как при прохождении соответствующей темы школьной программы, так и для подготовки к ЕГЭ (вторая часть).
Ещё данные показательные неравенства можно превратить в уравнения (заменяя знак неравенства знаком равенства). И использовать для прохождения темы “Решение показательных уравнений”.
Уникальность данной подборки заданий состоит в том, что она включает все типы неравенств, которые теоретически могут встретиться, а также к которым могут быть сведены сложные показательные неравенства.
Рекомендуется в каждом упражнении решать лишь некоторые неравенства. До усвоения применяемого метода.
Решение типовых показательных неравенств.
Неравенство, содержащее переменную в показателе степени, называют показательным. Иначе говоря, в показательных неравенствах присутствуют выражения вида 
, где а – некоторое число (
, 
), а f (x) – заданная функция.
Выше приведены так называемые типовые показательные неравенства. Типовыми данные неравенства называются в связи с тем, что их решение подчиняется четкому алгоритму. Но сначала давайте научимся решать показательные неравенства наиболее простых конструкций, то есть, простейшие.
Прежде всего, заметим, что показательное неравенство
(1)
при 
равносильно неравенству
, (2)
а при 
равносильно неравенству
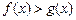. (3)
В более общем виде это же можно сформулировать так: для решения показательных неравенств вида
, 
, 
, 
нужно отбросить основания степени и перейти к равносильному неравенству [с показателями f (x) и g (x)] этого же знака при и неравенству противоположного знака при .
Пример. Решим следующие неравенства:
а) 
; б) 
; в) 
.
Решение.
а) Так как основание 5 > 1, то исходное неравенство равносильно следующему:
.
Продолжая равносильные преобразования, получим
.
б) Представим неравенство в виде
.
Так как основание 
, то последнее неравенство равносильно следующему:
.
Продолжая равносильные преобразования, получим
.
в) Чтобы привести неравенство к стандартному виду, нужно представить число 5 в виде степени с основанием 2. Но на этот раз для этой степени нельзя подобрать “нормальный” показатель и придется представить число в виде степени с логарифмическим показателем, воспользовавшись формулой
.
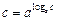Учитывая это, исходное неравенство принимает вид
.
Так как основание 2 > 1, то можно перейти к равносильному неравенству
.
Доведем решение до конца:
.
Ответ: а) 
; б) 
; в) 
.
В заключении отметим, что поскольку выражение ax положительно при любом значении x, то множество решений неравенств вида
, 
, и т. п.
есть x – любое число, а множество решений неравенств вида
, 
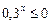и т. п.
является пустым (то есть, данные неравенства не имеют решений).
Здесь мы получили ответ, исходя из идеи учета области значения входящих в неравенство выражений. Применять данную идею можно, в частности, тогда, когда идея обычных преобразований неравенства в ему равносильное не проходит.
Давайте подведем предварительные итоги.
Простейшие показательные неравенства бывают двух видов:
, , ,
или
, 
, 
, 
.
В последнем случае с – некоторое неположительное число, то есть, 
.
Идея решения неравенств 1-го вида заключается в отбрасывании оснований степени и переходу к равносильному неравенству с показателями, то есть, функциями f (x) и g (x).
Идея решения неравенств 2-го вида состоит в учете области значения выражения , а именно, его положительности.
Очевидно, для решения любого показательного неравенства, его нужно свести к одному из простейших видов.
Познакомимся со спецификой неравенств каждого номера.
№ 1
Специфика заданий: показательное неравенство сводится к линейному.
Разберем для примера решение неравенства из № 1(о):
…
Ответ: 
№ 2
Специфика заданий: показательное неравенство сводится к квадратному.
Разберем для примера решение неравенства из № 2(д):
…
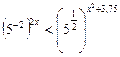
Ответ: 
.
№ 3
Специфика заданий: показательное неравенство сводится к дробно-рациональному. Как правило, дробно-рациональные неравенства решаются с помощью метода интервалов.
Разберем для примера решение неравенства из № 3(е):
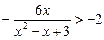
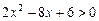
(последнее неравенство решаем графическим методом).
Ответ: 
.
Здесь мы воспользовались тем, что, так как выражение 
при любом значении x, то обе части неравенства
можно умножить на это выражение, сохранив при этом знака неравенства.
№ 4
Специфика заданий: показательное неравенство приводится к своему обычному виду (как в №№ 1 и 2) после вынесения степенного множителя за скобку.
Разберем для примера решение неравенства из № 4(л): 
.
С учетом того, что
,
выполним следующие равносильные преобразования:
.
Ответ: [1; + ∞).
Обратите внимание, что в примерах этого типа за скобку будет выноситься степенной множитель с наименьшим показателем. Соответственно, остальные степенные выражения должны быть через него предварительно выражены.
Например, в № 4(м) за скобку надо вынести множитель 
, а остальные степени 
, 
и 
через него выразить:
, и т. д.
Заметим также, что показательные неравенства из № 4 можно решать и путем замены переменной: обозначить буквой выносимый за скобку множитель. Тогда показательное неравенство сводится к линейному.
Упомянутый пример из № 4(л) в этом случае решается так:
Пусть 
, тогда 
и исходное неравенство приобретает вид
.
Выполняя равносильные преобразования, получаем
.
Теперь, возвращаясь к прежней переменной, получим
.
№ 5
Специфика заданий: показательное неравенство путем замены переменной сводится к квадратному.
Обратим особое внимание на то, что неравенства этого типа в отличие от ранее рассмотренных (из № 4) уже обязательно решаются методом замены переменной (или путем восприятия определенного выражения как переменной).
Суть этого метода состоит в том, что некоторое выражение с переменной обозначается новой буквой таким образом, чтобы исходное неравенство можно было преобразовать к более простому виду, причем содержащему только эту новую букву. Затем находится множество решений полученного таким образом нового неравенства, а потом и множество решений исходного неравенства.
Разберем для примера решение неравенства из № 5(ж):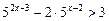 
.
Заметим, что если ввести замену
,
то выражение 
тоже можно выразить через новую букву (переменную t).
Действительно,
.
Поэтому
.
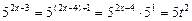Таким образом, исходное неравенство можно переписать в более простом виде:
.
Множество решений последнего неравенства:
.
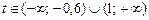Теперь возникает вопрос: как получить ответ для прежней переменной?
По полученному ответу нетрудно догадаться, что значение переменной t удовлетворяет одному из неравенств:
t < – 0,6 или t > 1.
Но это означает, что значение переменной х также удовлетворяет одному из неравенств:
или 
.
Запишем под каждым из этих неравенств его решение:
или 
нет решений, 
так как 
. x > 2.
Ответ: x > 2.
Принято говорить, что мы решали совокупность неравенств и 
, то есть, находили значения х, удовлетворяющие хотя бы одному из этих неравенств.
№ 6
Специфика заданий: показательное неравенство путем замены переменной сводится к дробно-рациональному, которое сразу же можно свести к квадратному.
Разберем для примера решение неравенства из № 6(а):
.
Далее вводя замену переменной 3 x = t, получаем неравенство
,
обе части которого можно умножить на t, поскольку новая переменная, как и заменяемое ею выражение 3 x, принимает только положительные значения.
Итак, последнее неравенство после умножение его обеих частей на t преобразуется в квадратное
t 2 + 27 ≥ 12 t,
множество решений которого есть
.
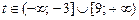От числовых промежутков перейдем к совокупности неравенств
t ≤ 3 или t ≥ 9.
Возвращаясь к прежней переменной, получаем совокупность неравенств
3 x ≤ 3 или 3 x ≥ 9.
Решим эту совокупность:
3 x ≤ 3 или 3 x ≥ 9
3 x ≤ 31 3 x ≥ 32
x ≤ 1 x ≥ 2
Ответ: x ≤ 1, x ≥ 2.
№ 7
Специфика заданий: показательное неравенство путем замены переменной сводится к дробно-рациональному, которое можно решить методом интервалов.
Разберем для примера решение неравенства из № 7(г):
.
Путем замены переменной 5 x = t преобразуем данное неравенство к виду
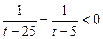
и, решая методом интервалов, находим
5 < t < 25.
После возвращения к прежней переменной, получаем
5 < 5 x < 25 51 < 5 x < 52 1 < x < 2.
№ 8
Специфика заданий: показательное неравенство путем однотипных преобразований сводится к уже ранее известному.
Разберем для примера решение неравенства из № 8(б):
.
После деления обеих частей последнего неравенства на положительное выражение 4 x получим
;
последнее же неравенство может быть сведено к квадратному путем замены 
.
Доделайте задание самостоятельно.
Ответ: 
.
Разберем ещё решение неравенства из № 8(з):
;
поделив числитель и знаменатель дроби в последнем неравенстве на 2 x, получаем равносильное неравенство
,
которое сводится к дробно-рациональному путем замены переменных .
Доделайте задание самостоятельно.
Ответ: 
.